Program verzió: Consteel 17; Build 3303 

Tervezés célja, tervezési szabvány kiválasztása

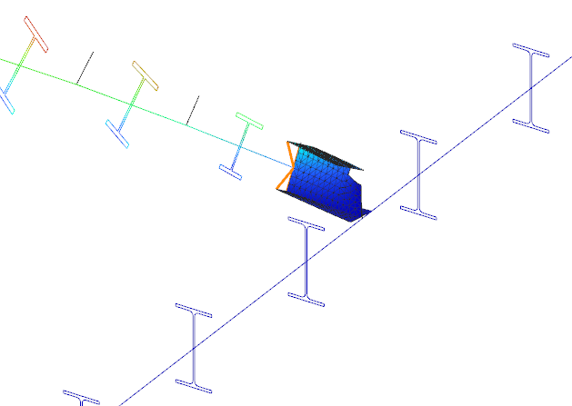
A jelen tervezési segédlet a kezdő ConSteel 17 felhasználó számára egy kéttámaszú rácsos tartó tervezését mutatja be, lépésről lépésre. Az építészeti koncepcionális tervből ismert a megtervezendő rácsos tartó geometriai kialakítása (1. ábra). A koncepció szerint a rácsos tartó övei HEA120 típusú melegen hengerelt szelvényből készülnek, míg a rácsrúdjai hidegen alakított SHS80x4 szelvényből. A jelen segédletnek a csomópontok tervezése nem része.

Ismert, hogy a szerkezettervezés mindig valamely szabvány, illetve annak változata szerint történik. A szabvány kiválasztása új modell létrehozásakor a Project centerben a Tervezési szabvány menüből választható, vagy később a Szabványok rendszerfül [S1] kiválasztó paneljében módosítható (2. ábra).

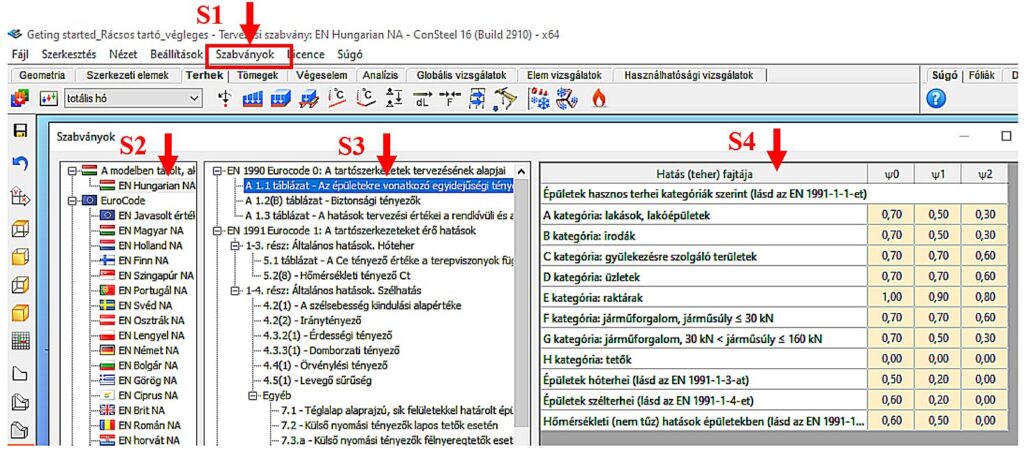
Az alkalmazni kívánt tervezési szabvány a panel bal oldali listájából választható ki. Jelen esetben az EN Hungarian NA opciót [S2] választjuk (MSz EN Magyar Nemzeti melléklet). A kiválasztott szabvány által alkalmazott paraméterek a középső tartalomjegyzék megfelelő sorának kiválasztásával érthető el, a jobb oldali táblázatban [S4]. A 2. ábrán az EC0 szabvány 1.1 táblázatának megfelelő egyidejűségi tényezők kerültek kiválasztásra, amely paramétereket a jobb oldali táblázat mutatja meg.

Szerkesztő raszter beállítása

Először állítsuk be a raszter méretét a szerkezet fesztávjának megfelelően. Ehhez alkalmazzuk a baloldalon található eszközcsoport megfelelő gombját [1], amelynek hatására megjelenik a Raszterháló és koordinátarendszer beállító panel (2. ábra).

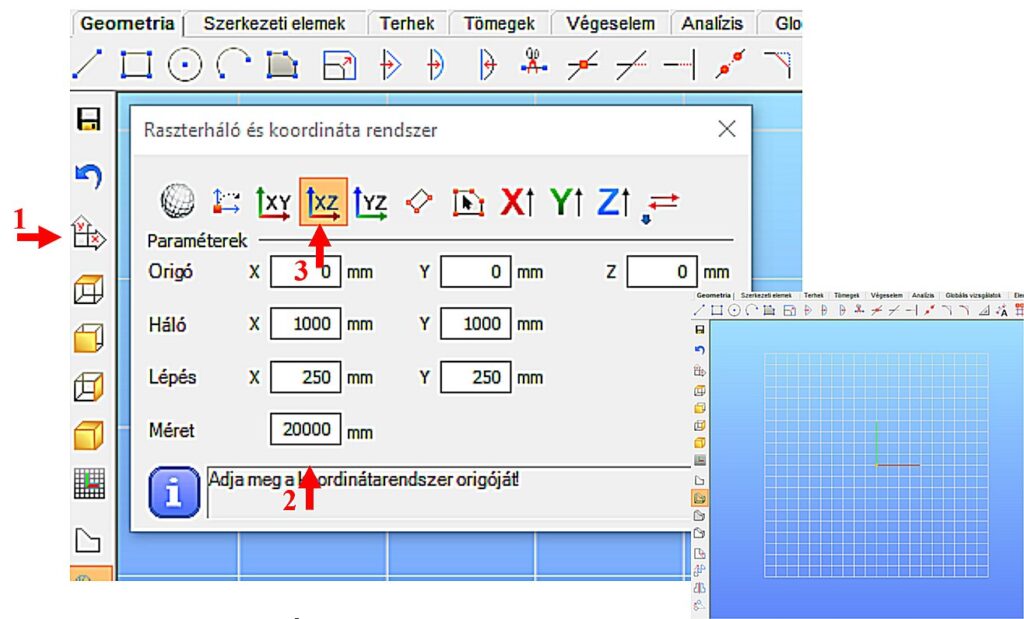
Például a 19.6m hosszú tartó esetén a Méret ablak tartalmát 20000 milliméterre állíthatjuk [2]. A beállítás aktualizálásához nyomjuk meg az Enter-t, vagy zárjuk be az ablakot. A fenti beállítás esetén a raszter X és Y irányban 20 méter széles lesz, a raszter vonalak sűrűsége 1000 mm, a lépésközök 250 mm. A rácsos tartó modellt célszerű az X-Z globális koordináta síkban felvenni, tehát a szerkesztő rasztert el kell fordítanunk az X-Z síkba. Ehhez válasszuk XZ sík opciót [3].

gate

Consteel recommends to use the General Method from EN 1993-1-1 for the evaluation of out-of-plane strength of members and sturctures. In addition, the scaled imperfection based 2nd order approach is available.

Did you know, that when linear buckling eigenform affine imperfections are used, Consteel can scale automatically the selected eigenmodes to perform a Eurocode compatible design? And you can even combine several imperfections?

Download the example model and try it!

Bending:

Download model

Copmression:

Download model

If you haven’t tried Consteel yet, request a trial for free!

Try Consteel for free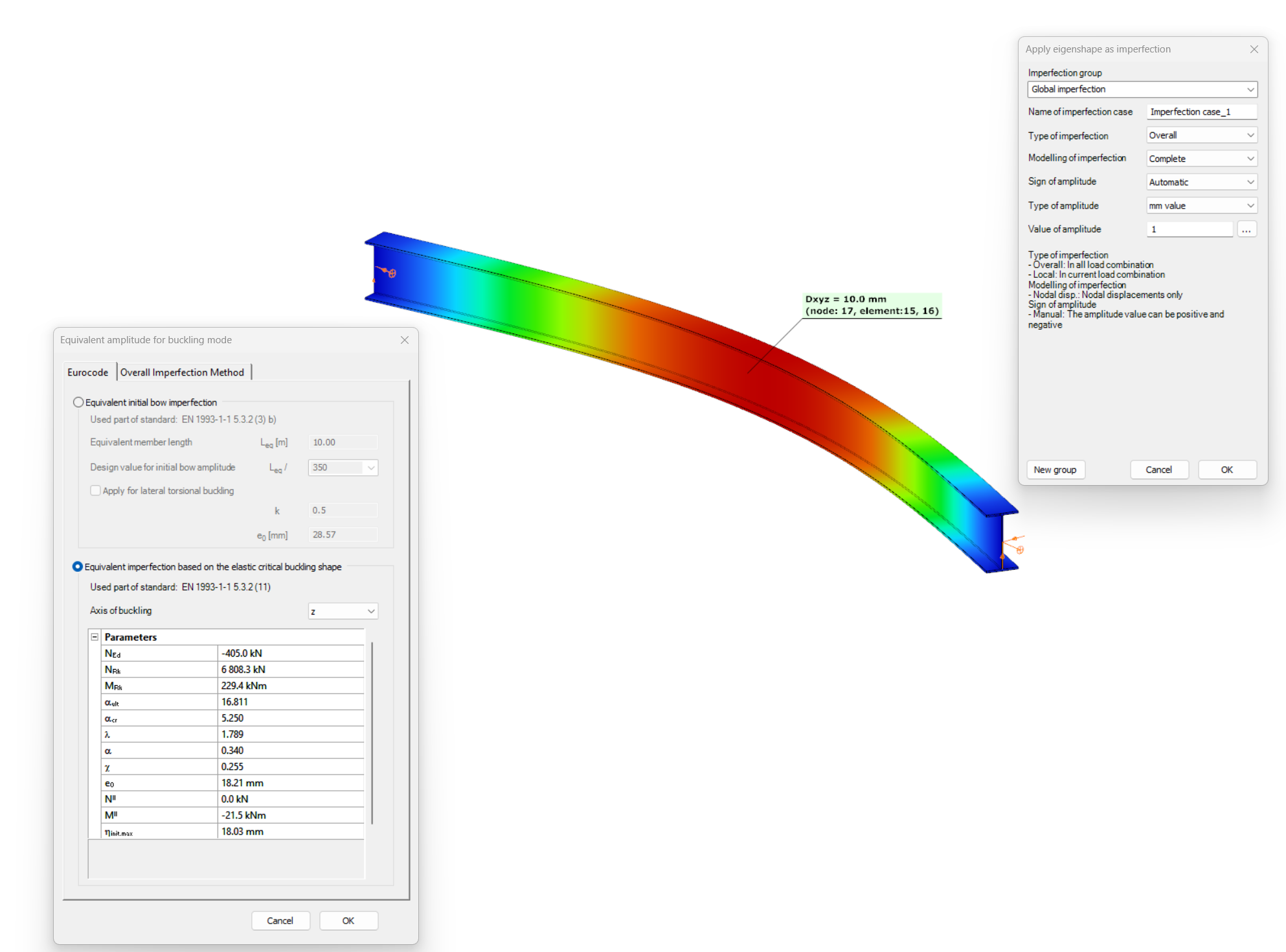

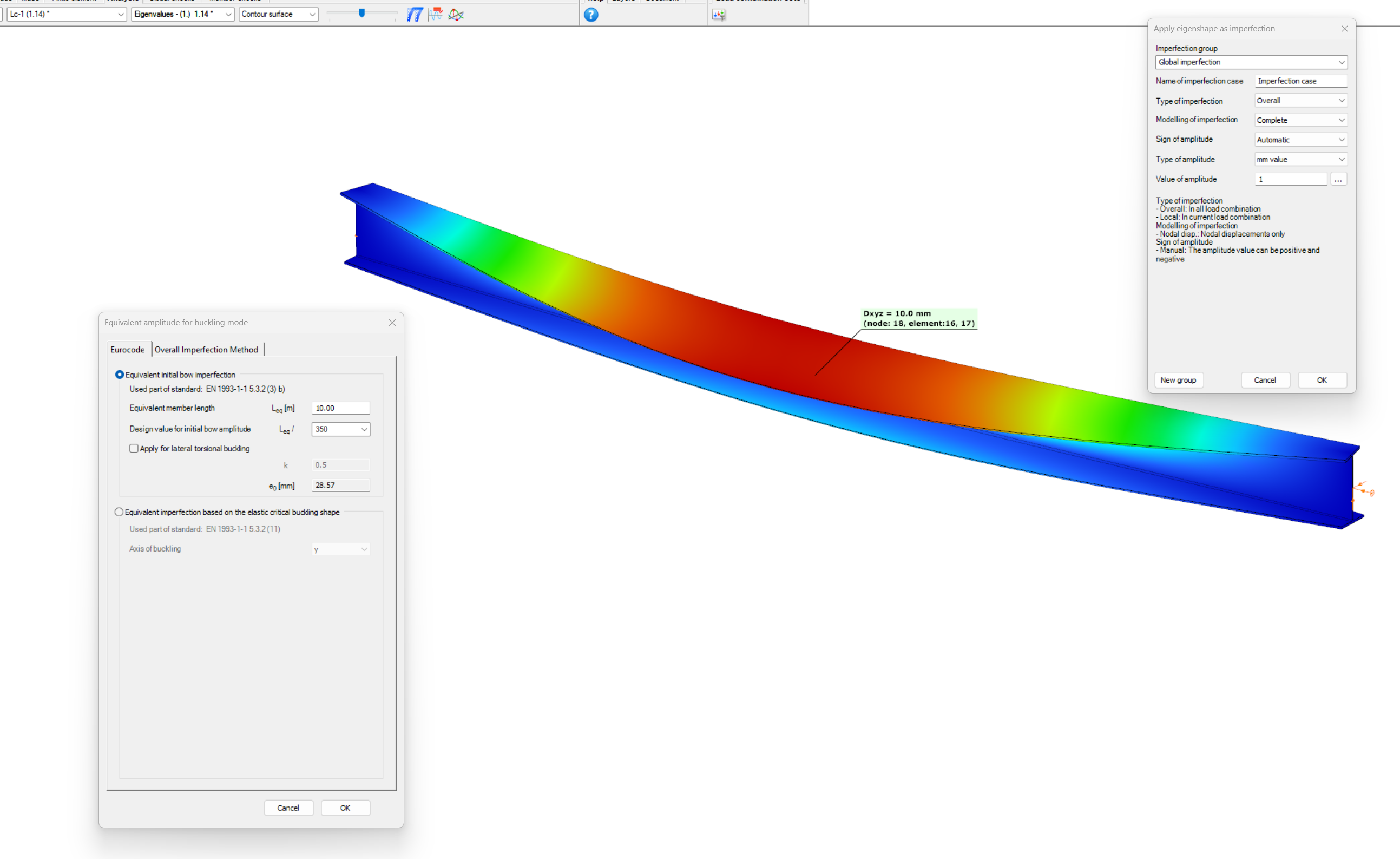
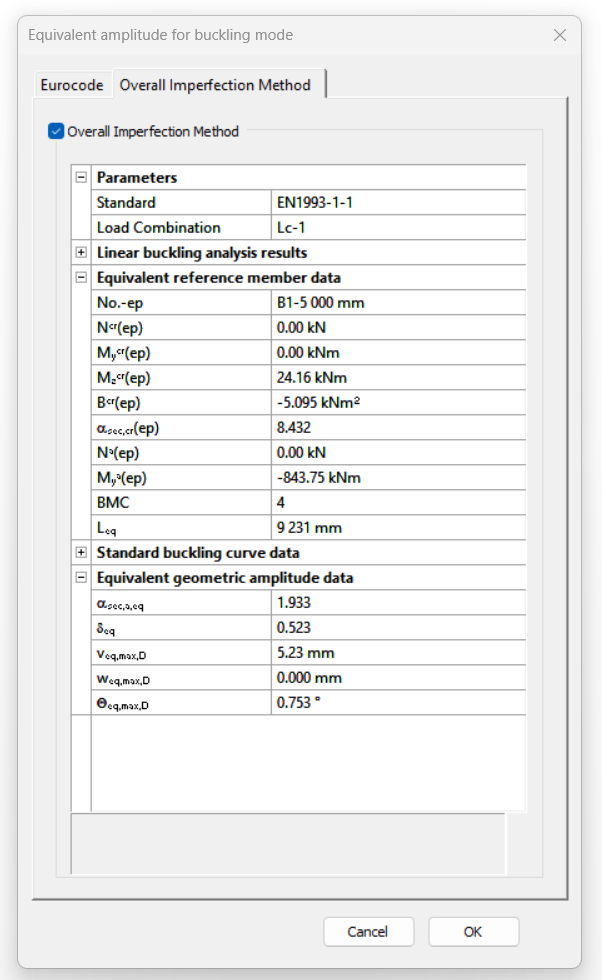
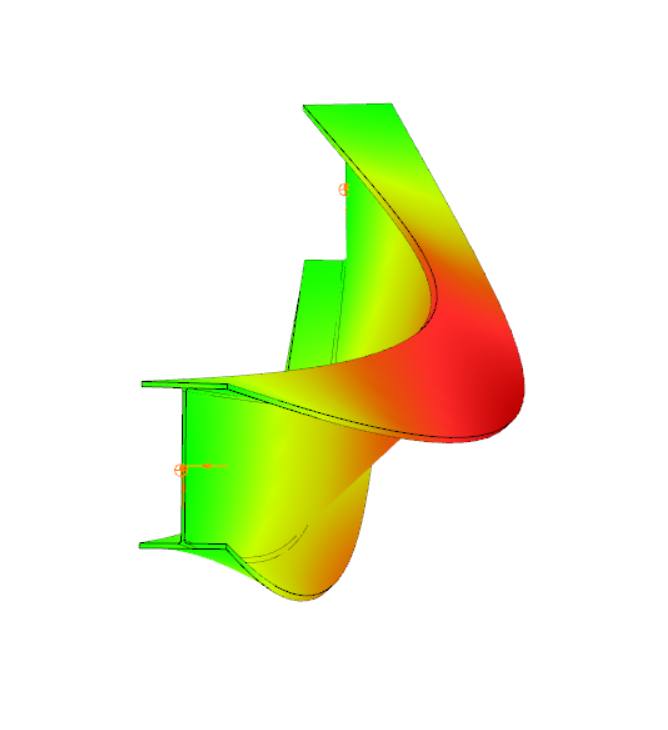
Have you ever heard about the ‘General Method’? This is an alternative design method to consider the interaction of axial compression with major-axis bending for general buckling situations, where the main interaction formulas are not applicable.

This basically includes every member with monosymmetric or asymmetric cross-sections or with cross-sections not uniform along the length (welded tapered sections) or laterally stabilized by sheeting or anything else without providing full fork supports.

Did you know, that the General Method is fully supported by Consteel and provides an automated buckling verification possibility? Of course, for the use of the General Method in a general case the traditional 12DOF beam finite elements are not applicable. But the special 14DOF beam elements used by Consteel are perfectly compatible? 

Download the example model and try it!

Download model

If you haven’t tried Consteel yet, request a trial for free!

Try Consteel for free

Bevezetés

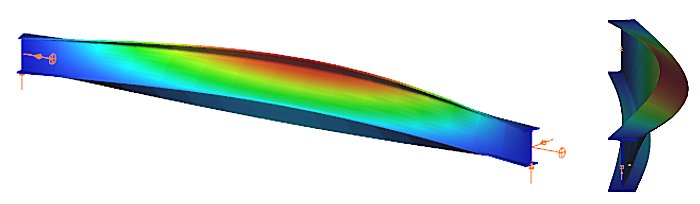
Amennyiben a síkban hajlított gerenda szabadon elmozdulhat és elcsavarodhat a két támaszpontja között, akkor a lehajlás mellett hirtelen merőleges elmozdulás és elcsavarodás jöhet létre: a gerenda kifordul a síkjából. Ezt a jelenséget szemlélteti az 1. ábra, amely egy kéttámaszú, az erős tengely körül hajlított I keresztmetszetű gerendát mutat: a függőleges síkban történő hajlítás során, amikor a nyomaték elér egy kritikus értéket, a gerenda hirtelen oldalirányban elmozdul és elfordul a két támasz között. Ez a jelenség a kifordulás, amely stabilitásvesztési mód a tökéletes gerendára és a valódi gerendára egyaránt vonatkozhat.

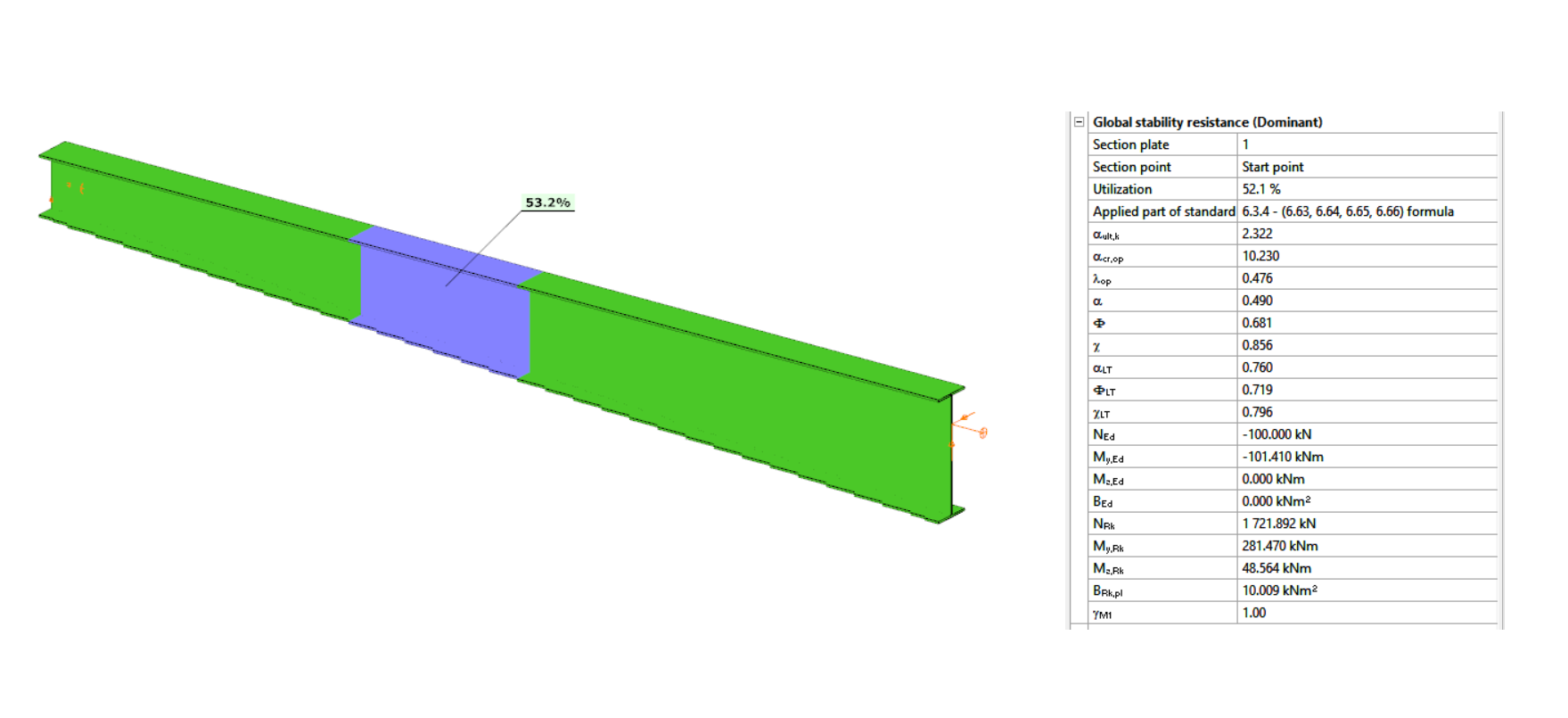
A gerenda kifordulással szembeni méretezése teljes mértékben analóg a nyomott oszlop kihajlási elleni méretezésével. Az analógiát az 1. táblázat szemlélteti, ahol feltüntettük a kihajlási és a kifordulási ellenállást befolyásoló, egymásnak megfelelő paramétereket.

Kihajlás	Kifordulás
tervezési nyomóerő ($N_{Ed}$)	tervezési nyomaték ($M_{Ed}$)
kritikus erő ($N_{cr}$)	kritikus nyomaték ($M_{cr}$)
kihajlási karcsúság ($\frac{}{\lambda}$)	kifordulási karcsúság ($\frac{}{\lambda}_{LT}$)
kihajlási csökkentő tényező ($\chi$)	kifordulási csökkentő tényező ($\chi_{LT}$)
kihajlási ellenállás ($N_{b,Rd}$)	kifordulási ellenállás ($M_{b,Rd}$)

A tökéletes gerenda kritikus nyomatékát a M_y,Edtervezési hajlítónyomaték-diagram maximális értékének helyén kell meghatározni. Kétszeresen szimmetrikus I keresztmetszet esetén:

$$M_{cr}=C_1\frac{\pi^2EI_z}{(k_z⋅L)^2}\left[\frac{I_\omega }{I_z}+ \frac{(k_zL)^2GI_t}{\pi^2EI_z}\right] ^{0.5} $$

ahol k_z a keresztmetszet gyenge tengelye körüli befogási tényező, G a nyírási modulus, I_t és I_ω pedig a keresztmetszet tiszta (St. Venant) és gátolt csavarási tehetetlenségi nyomatéka. A C₁ tényező értéke a hajlító nyomatéki diagram alakjától függ, az értéke megfelelő táblázatokban és kézikönyvekben megtalálható. Konstans nyomatéki ábra esetén C₁=1.0. A többi tervezési paraméter, különösen a $\chi_{LT}$ kifordulási csökkentő tényező képlete a figyelembe vett tervezési szabványtól függ.

Kifordulási ellenállás az EN1993-1-1 szerint  

A hajlított gerenda kifordulás elleni méretezését (teherbírás-ellenőrzést) az EC3-1-1 szerint a következő lépésekben kell elvégezni:

gate

Rácsos tartó szerkezet méretezése

A rácsos tartók globális (rúdszerkezeti szintű) méretezése nem igényel különleges elméleti ismeretet: rendszerint a hajlítónyomatékok és a nyíróerők elhanyagolásával a rácsos tartók rudjait nyomott és/vagy húzott rúdként méretezzük. A nyomott rudak méretezését manapság modell alapú számítógépes eljárással hajtjuk végre. Ennek részleteit lásd a Nyomott rúd méretezése kihajlás ellen című tudásbázis anyagban. Itt csak a nyomott rudak kihajlási hosszának meghatározását mutatjuk be.

A nyomott rúd méretezésénél a legfontosabb paraméter a rúdkarcsúság:

$$\overline{\lambda}=\sqrt\frac{Af_y}{N_{cr}}$$

ahol

$$N_{cr}=\frac{\pi^2El}{(kL)^2}$$

ahol a k kihajlási hosszt (befogási tényezőt) az EN1993-1-1 szabvány, a kézi számítások megkönnyítése érdekében, az alábbiak szerint javasolja felvenni:

Nyomott rúd típusa	Kihajlás iránya	k
övrúd	– tartó síkjában – tartó síkjára merőlegesen	0.9 0.9
rácsrúd	– tartó síkjában – tartó síkjára merőlegesen	0.9 1.0

A modell alapú számítógépes eljárásokon alapuló szoftverek (pl. a Consteel szoftver) a fenti konzervatív szabály helyett az N_cr rugalmas kritikus erőt közvetlenül végeselemes numerikus módszerrel, a teljes rácsos tartó viselkedésének figyelembe vételével, határozzák meg. Az alábbi példával a szabvány által javasolt kézi méretezési eljárás és a modern, modell alapú numerikus eljárás eredményének viszonyát kívánjuk szemléltetni.

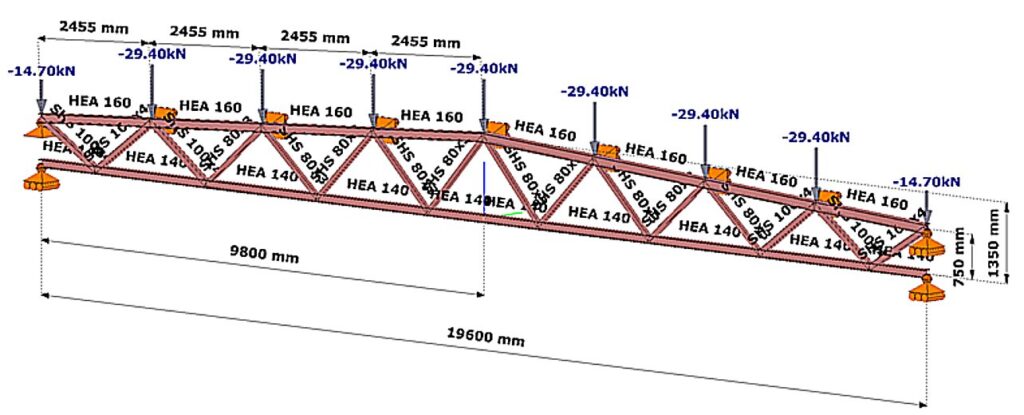
• Legyen a vizsgált rácsos tartó szerkezeti modellje az 1. ábrán látható Consteel modell.
• A feltűntetett teher feleljen meg a tartó mértékadó tervezési teherkombinációjának.
• Határozzuk meg a legjobban igénybe vett nyomott övrúd kihajlási hosszát végeselemes numerikus stabilitási analízis segítségével.

Eljárások összehasonlítása

A számítás lépései a következők:

Rugalmas stabilitási analízis

A rugalmas modell stabilitási analízise megmutatja, hogy a rácsos szerkezet mértékadó stabilitásvesztési módját és az ahhoz tartozó α_cr rugalmas kritikus teherszorzót (2. ábra).

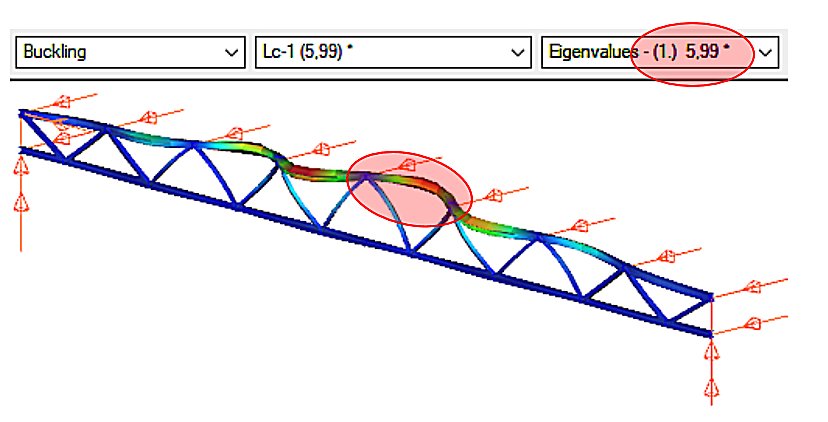
Láthatjuk, hogy a terhelés hatására a tökéletesen rugalmas modell felső öve oldalsó irányban kihajlást szenved. A teher, amely hatására a rugalmas kihajlás bekövetkezik, a kritikus teher, amelynek értékét a tervezési teher és az α_cr=5.99 kritikus teherszorzó szorzata adja meg.

gate

A nyomott rúd méretezésének fejlődése

A rudakból épített acélszerkezetek (pl. rácsos tartók) egyik jellegzetes alkotó eleme a nyomott rúd.  Nyomott rúdról akkor beszélünk, ha a rendszerint egyenes tengelyű szerkezeti elem központos P nyomóerővel terhelt (1. ábra).

A 2. ábra a nyomott rúd méretezésének fejlődését illusztrálja.  Kezdetben (a régi időkben) az építőmesterek az évszázadok során felhalmozódott tapasztalati ismeretek alapján, amelyek mesterről tanítványra szálltak, állapították meg a különböző anyagú és méretű nyomott oszlopok teherbírását. Jelentős változást a klasszikus matematikai differenciálanalízis mérnöki alkalmazása hozott. Euler (1707-1783) svájci matematikus és fizikus megoldotta a nyomott rugalmas vonal kihajlásának problémáját, amely megoldás alkalmazható volt a rugalmas nyomott rúd megoldására (Euler erő). A mérnökök a következő évszázadokban felismerték, hogy az Euler erő csak bizonyos esetekben (elsősorban nagy karcsúságoknál) ad elfogadható közelítést a nyomott rúd valós teherbírására. Számos, az Euler képletnél fejlettebb megoldás született a nyomott rúd teherbírására, de jelentős változást csak a II. világháborút követő hatalmas szerkezetépítési konjunktúra hozott. A világ minden számottevő szerkezeti laboratóriumában sorra végezték a nyomott rúd kísérleteket, majd az eredményekből összeállítottak egy több mint kétezer kísérletből álló adatbázist. A nyomott rúd teherbírását az adatbázis alapján, a matematikai statisztika módszerével meghatározott képlettel adták meg.

Ez a módszertan a mai napig meghatározó: „a nyomott rúd méretezése az acélszerkezeti szakma politikai kérdése lett…”. Ezért a nyomott rúd méretezési elvének megértése a szerkezet-építőmérnök számára alapvető fontosságú.

Az ábra jobb oldala a jövőre is tartalmaz utalást. A tudományos kutatás szintjén már jelen, hogy a valós nyomott rúd teherbírását matematikai-mechanikai szimulációval is meg lehet határozni. Sőt, a közeljövőben minden eddigi ismeretet meghaladó adatbázisok hozhatók létre a szuperszámítógépek bevetésével. Egy ilyen gigantikus adatbázis alapján a mesterséges intelligencia felülírhatja az eddigi mérnöki tudást és módszertant, legalábbis elvben. A valóság viszont az, hogy a szerkezet-éptőmérnökség nem tartozik a húzóágazatok közé (mint például a hadipar vagy az autóipar), ezért ez az új méretezéselméleti váltás még egy jó ideig bizonyosan várat magára.

A továbbiakban a ma acélszerkezeti mérnöksége számra kiemelten fontos Euler erőt és a kísérleti alapú szabványos méretezési formulát tárgyaljuk részletesen.

Az ideális nyomott rúd teherbírása: az Euler erő

Tételezzük fel, hogy az alábbi ábrán látható csuklósan megtámasztott nyomott rúd rendelkezik az alábbi tulajdonságokkal:

• tökéletesen egyenes,
• az anyaga tökéletesen lineárisan rugalmas,
• központosan nyomott.

A fenti feltételekkel végezzük el a nyomott rúd kísérletet a Consteel szoftver segítségével: futtassuk a lineáris kihajlási analízis (Linear Buckling Analysis, LBA) számítást. Az eredményt a 3. ábra szemlélteti.

gate

Did you know that you could use Consteel to perform dual analysis with 7DOF beam and/or shell elements?

With two advanced features, Superbeam and Convert members to plates, you can choose the approach that best suits your project needs, whether you’re focused on modeling efficiency or detailed analysis.

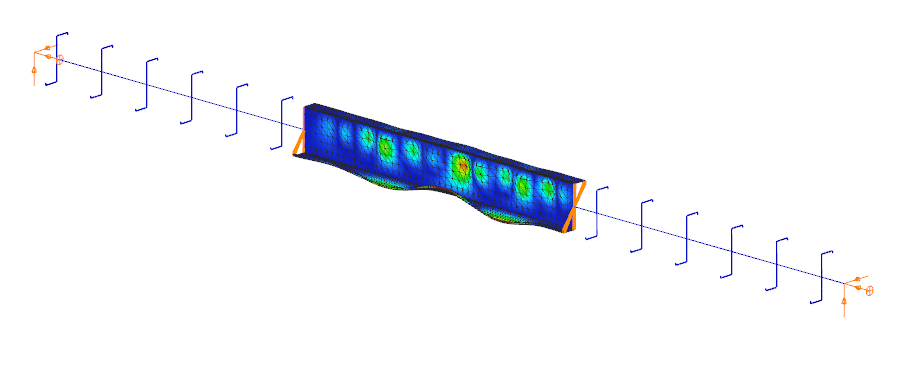
The Superbeam function offers a smart, adaptive way to handle structural members. It enables you to model with the simplicity of standard 7DOF beam elements while allowing you to switch to a more detailed shell-based analysis for specific members whenever needed.

Once the structure is modeled using beam elements, you can select how each member is analyzed:

• Using the beam model, which applies Consteel’s proven 7DOF beam elements along with its comprehensive design tools.
• Or using a shell model, which is automatically generated for selected members. This shell model includes detailing features such as web cutouts and stiffeners, fully integrated into the global analysis model.

This dual approach is fully adaptive. You can continue modifying your model using beam elements and switch between analysis modes as required, offering both speed and precision within the same workflow.

For a complete overview of how to activate and manage Superbeam functionality, refer to the documentation:
Superbeam – Consteel Manual

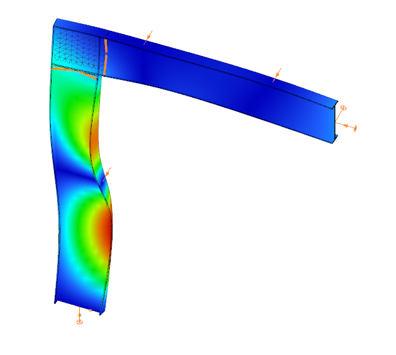
When you need complete control over geometry and mesh, or when shell analysis alone is not sufficient, Consteel provides the Convert members to plates function. This tool allows you to manually transform selected members into actual plate elements, enabling detailed modeling from the start.

Unlike the automatic conversion used in Superbeam, this method performs a permanent, non-reversible transformation (though undo is available during the session). It supports a wide range of section types, including hot-rolled, cold-formed, and welded profiles.

The conversion process preserves and adapts existing connections, eccentricities, loads, and supports. Where needed, rigid bodies and constraint elements are added to maintain structural continuity. These constraints ensure proper transfer of deformations, including warping, between the new plate model and the rest of the structure.

This function is especially useful in cases where precision is critical, such as modeling joints, fabrication-specific details, or complex load interactions.

To learn more, see the full guide here:
Convert Members to Plates – Consteel Manual

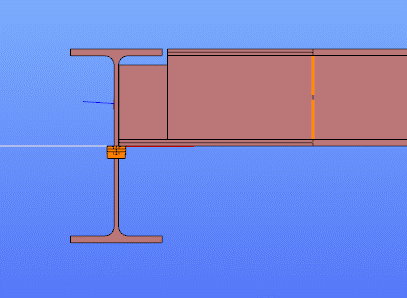
Both Superbeam and Convert members to plates serve different purposes, depending on the level of detail and control required in your model:

Feature	Superbeam	Convert members to plates
Workflow	Beam modeling with optional shell analysis	Full plate modeling from the beginning
Conversion	Automatic and reversible	Manual and permanent
Suitable For	Flexibility in analysis, quick modeling	Full control, high-detail requirements
Supported Sections	Welded I and H profiles	Hot-rolled, cold-formed, and welded sections
Detailing Support	Cutouts and stiffeners (in shell analysis)	Full geometric detailing, including transitions
Design Integration	Integrated with beam-based design tools	Suitable for fabrication-level modeling

In Superbeam, constraint elements are generated automatically to connect converted shell elements to other members, such as bars. During member-to-shell conversion, these elements link the FE shell nodes to the rest of the model, ensuring accurate deformation transfer.

If the convert members to plate function is applied directly to beam elements, rigid bodies are created at their ends, which is useful for analyzing local behavior but does not transfer warping deformations. If the beam is first converted to a shell and then to plates, hinged rigid edges are placed along the plate boundaries. This arrangement, combined with constraint elements, transfers not only in-plane and out-of-plane deformations but also warping between the shell and the rest of the structure.

Download the example model and try it!

Download model

If you haven’t tried Consteel yet, request a trial for free!

Try Consteel for free

Did you know that you could use Consteel to consider connection stiffness for global analysis?

One of Consteel’s unique strengths is its ability to integrate joint modeling and calculation directly into the global analysis.

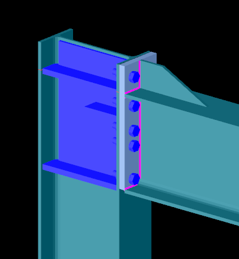
The Joint module performs all analyses in line with the standard procedures of Eurocode 3 Part 1-8, covering almost the entire scope of the code. This ensures results that are both reliable and fully compliant, across a wide range of connection types such as: Moment connections, Shear connections, Hollow section connections.

Modern structural design increasingly considers the mechanical interaction between the global model and its joints — whether rigid, semi-rigid, or pinned.

This integrated approach leads to results that are both more realistic and more economical, but it also requires more sophisticated modeling. Consteel makes this process straightforward:

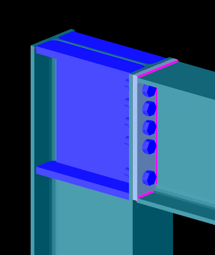
• Joints can be created manually or automatically based on the model geometry.
• The create joint by model function examines member positions and cross-sections, then offers suitable joint types.
• Once defined, the joint can be placed into the global model, and its connection stiffness can be included in the global analysis.
• After placement, the joint is always rechecked against the latest analysis results.

In order to consider the connection stiffness of the placed joint, open the analysis parameters, tick the Include connection stiffness checkbox, and rerun the analysis.

Let’s explore how the behavior of a simple frame changes under different connection assumptions:

In the first case, where no actual connection stiffness was considered and the members were assumed to have continuous rigid ends, the results showed a bending moment (My) of 129.23 kNm at the column upper end and 115.25 kNm at the beam midspan. The corresponding deflection in the beam’s midspan (z-direction) was –17.4 mm.

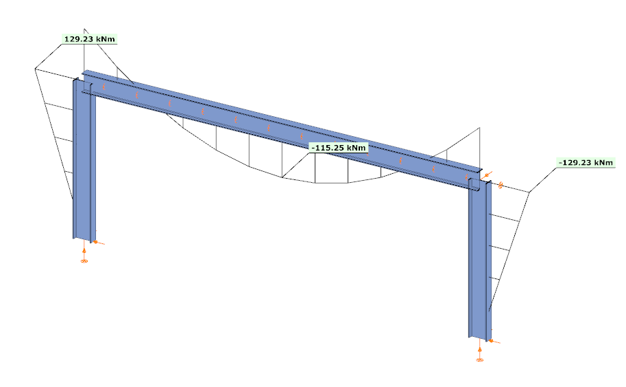
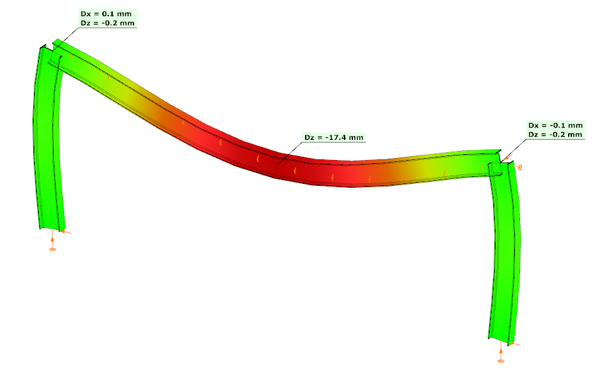
In the second case, the connections were modeled with their actual semi-rigid stiffness of 29.8% and partial strength. Here, the bending moment at the column upper end decreased to 90.45 kNm, while the beam midspan moment increased to 154.03 kNm. The beam midspan deflection reached –26.5 mm, representing an increase of 52% compared to the rigid assumption.

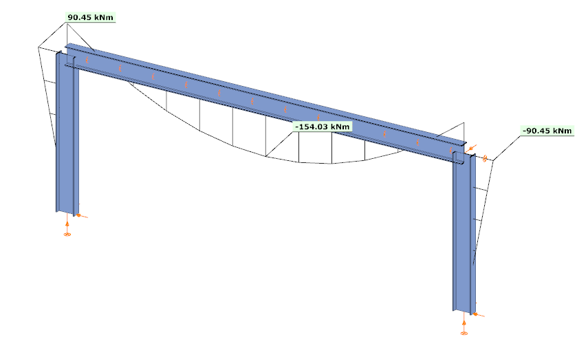
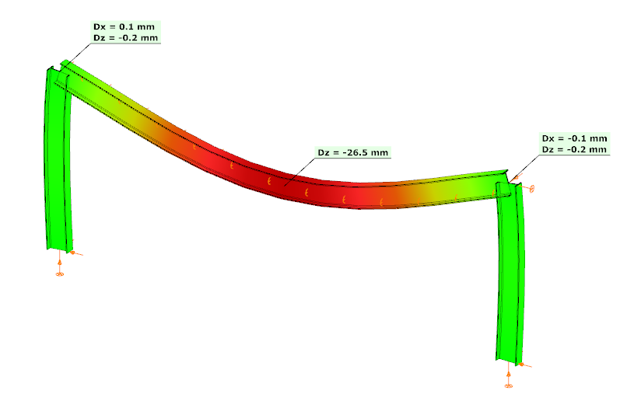
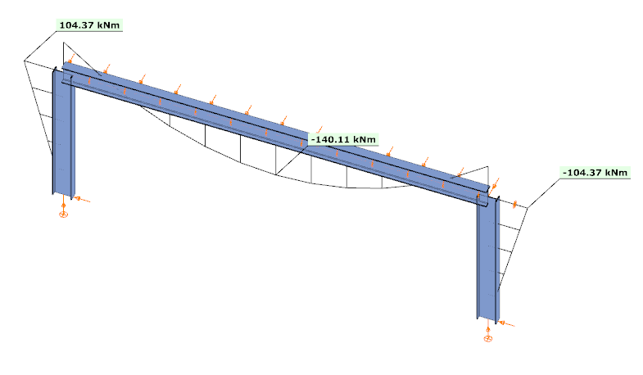
In the third case, with a higher semi-rigid stiffness of 53.6% and partial strength, the results balanced between the two extremes: the column end moment was 104.37 kNm, the beam midspan moment was 140.11 kNm, and the midspan deflection was –23.2 mm. This corresponds to an increase of 33% in deflection compared to the rigid assumption.

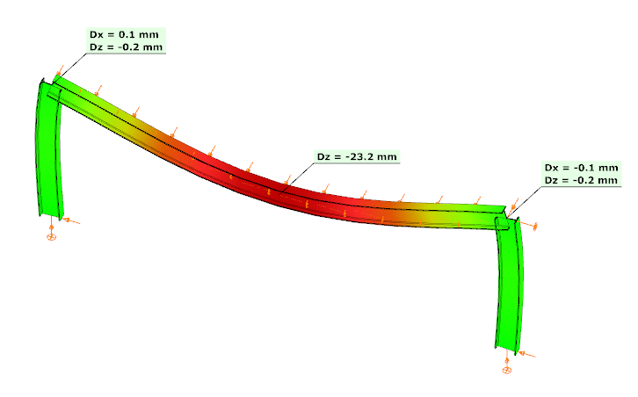
These examples clearly demonstrate how connection stiffness significantly influences global structural behavior. Assuming rigid connections may underestimate beam deflections and distort moment distribution, while considering realistic semi-rigid stiffness, provides a more accurate representation of structural performance.

Download the example model and try it!

Download model

If you haven’t tried Consteel yet, request a trial for free!

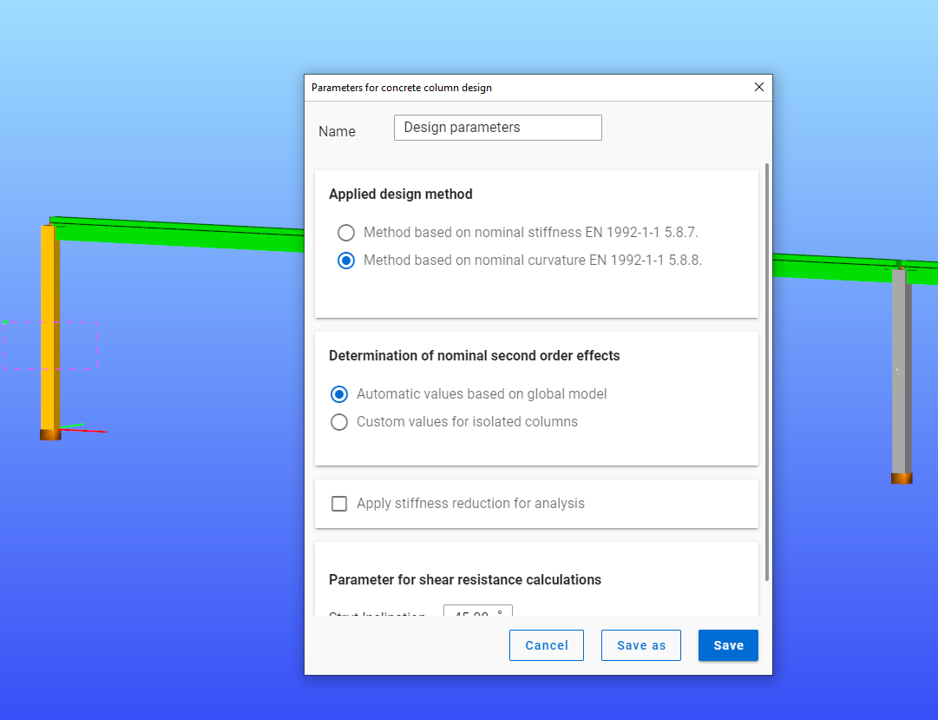
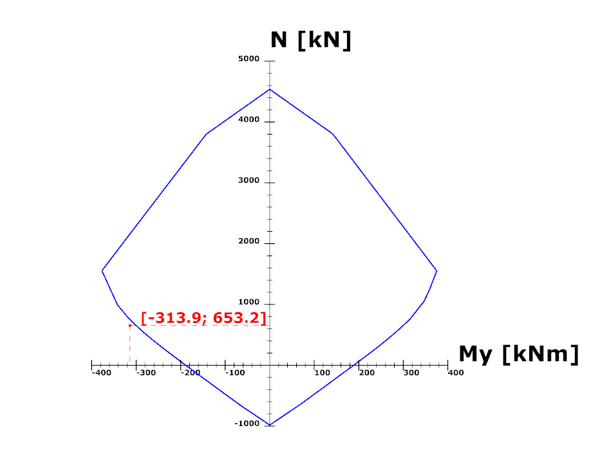
Try Consteel for free

Did you know that you could use Consteel to determine automatically the second order moment effects for slender reinforced concrete columns?

Download the example model and try it!

Download model

If you haven’t tried Consteel yet, request a trial for free!

Try Consteel for free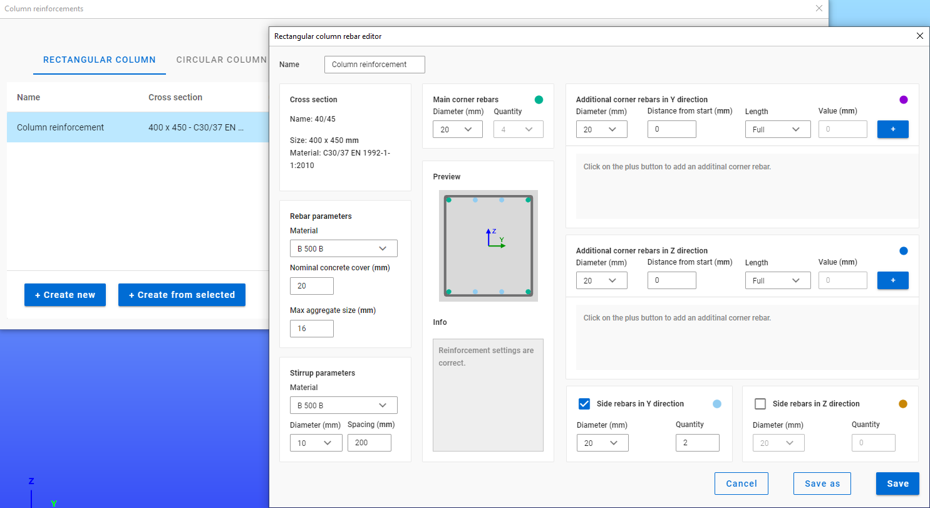

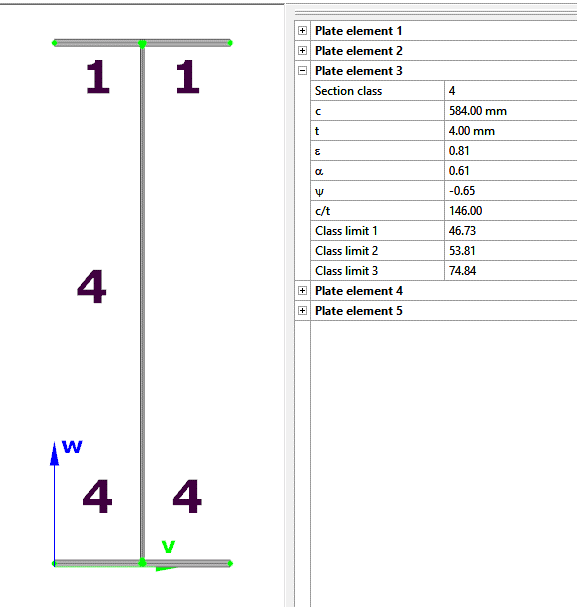
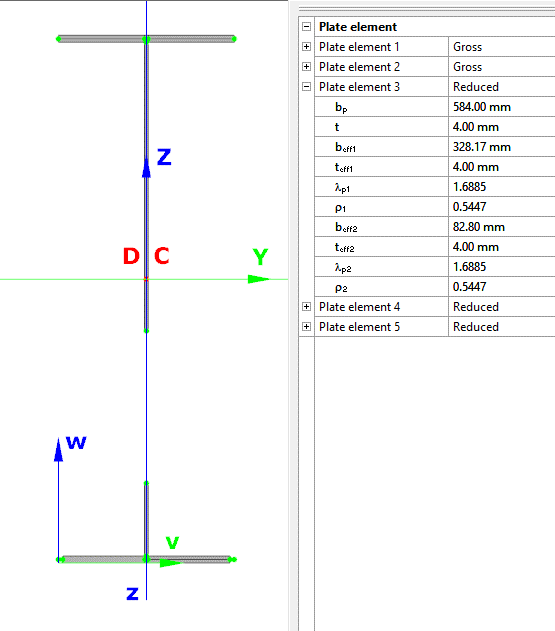
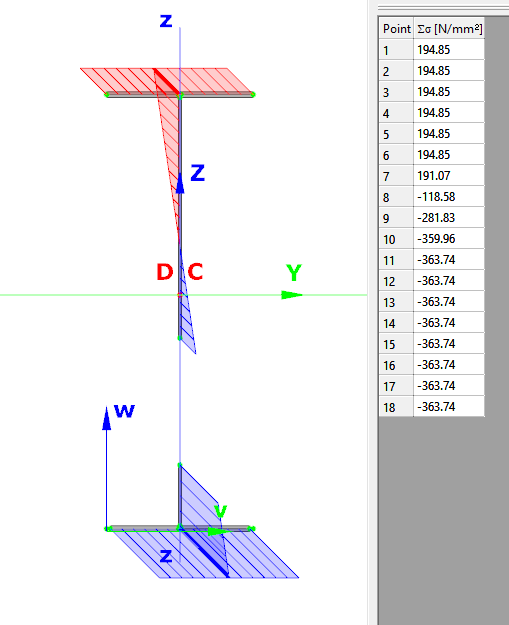
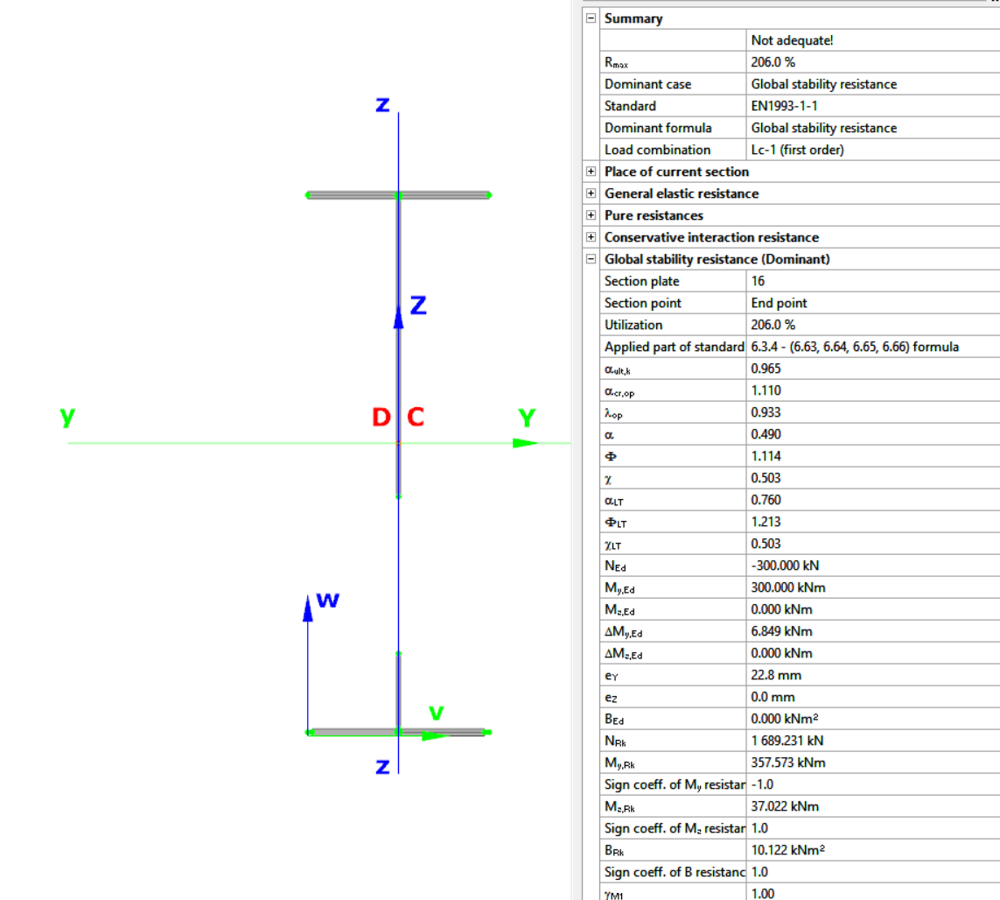
Did you know that you could use Consteel to calculate effective cross-section properties for Class 4 sections?

Download the example model and try it!

Download model

If you haven’t tried Consteel yet, request a trial for free!

Try Consteel for free