Program verzió: Consteel 17; Build 3303
Tervezés célja, tervezési szabvány kiválasztása
A jelen tervezési segédlet a kezdő ConSteel 17 felhasználó számára egy kéttámaszú rácsos tartó tervezését mutatja be, lépésről lépésre. Az építészeti koncepcionális tervből ismert a megtervezendő rácsos tartó geometriai kialakítása (1. ábra). A koncepció szerint a rácsos tartó övei HEA120 típusú melegen hengerelt szelvényből készülnek, míg a rácsrúdjai hidegen alakított SHS80x4 szelvényből. A jelen segédletnek a csomópontok tervezése nem része.
Ismert, hogy a szerkezettervezés mindig valamely szabvány, illetve annak változata szerint történik. A szabvány kiválasztása új modell létrehozásakor a Project centerben a Tervezési szabvány menüből választható, vagy később a Szabványok rendszerfül [S1] kiválasztó paneljében módosítható (2. ábra).
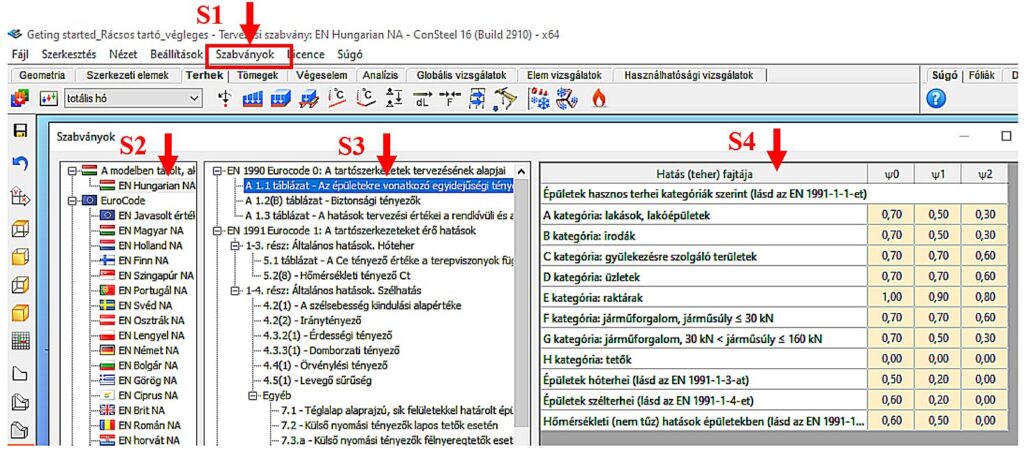
Az alkalmazni kívánt tervezési szabvány a panel bal oldali listájából választható ki. Jelen esetben az EN Hungarian NA opciót [S2] választjuk (MSz EN Magyar Nemzeti melléklet). A kiválasztott szabvány által alkalmazott paraméterek a középső tartalomjegyzék megfelelő sorának kiválasztásával érthető el, a jobb oldali táblázatban [S4]. A 2. ábrán az EC0 szabvány 1.1 táblázatának megfelelő egyidejűségi tényezők kerültek kiválasztásra, amely paramétereket a jobb oldali táblázat mutatja meg.
Szerkesztő raszter beállítása
Először állítsuk be a raszter méretét a szerkezet fesztávjának megfelelően. Ehhez alkalmazzuk a baloldalon található eszközcsoport megfelelő gombját [1], amelynek hatására megjelenik a Raszterháló és koordinátarendszer beállító panel (2. ábra).
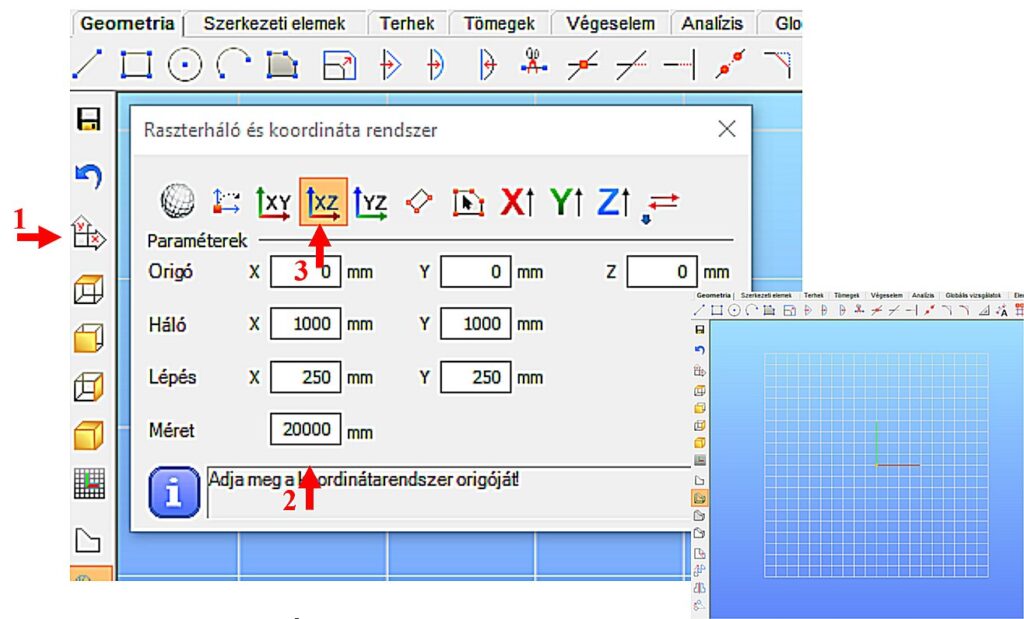
Például a 19.6m hosszú tartó esetén a Méret ablak tartalmát 20000 milliméterre állíthatjuk [2]. A beállítás aktualizálásához nyomjuk meg az Enter-t, vagy zárjuk be az ablakot. A fenti beállítás esetén a raszter X és Y irányban 20 méter széles lesz, a raszter vonalak sűrűsége 1000 mm, a lépésközök 250 mm. A rácsos tartó modellt célszerű az X-Z globális koordináta síkban felvenni, tehát a szerkesztő rasztert el kell fordítanunk az X-Z síkba. Ehhez válasszuk XZ sík opciót [3].
gateRácsos tartó szerkezet méretezése
A rácsos tartók globális (rúdszerkezeti szintű) méretezése nem igényel különleges elméleti ismeretet: rendszerint a hajlítónyomatékok és a nyíróerők elhanyagolásával a rácsos tartók rudjait nyomott és/vagy húzott rúdként méretezzük. A nyomott rudak méretezését manapság modell alapú számítógépes eljárással hajtjuk végre. Ennek részleteit lásd a Nyomott rúd méretezése kihajlás ellen című tudásbázis anyagban. Itt csak a nyomott rudak kihajlási hosszának meghatározását mutatjuk be.
A nyomott rúd méretezésénél a legfontosabb paraméter a rúdkarcsúság:
$$\overline{\lambda}=\sqrt\frac{Af_y}{N_{cr}}$$
ahol
$$N_{cr}=\frac{\pi^2El}{(kL)^2}$$
ahol a k kihajlási hosszt (befogási tényezőt) az EN1993-1-1 szabvány, a kézi számítások megkönnyítése érdekében, az alábbiak szerint javasolja felvenni:
| Nyomott rúd típusa | Kihajlás iránya | k |
|---|---|---|
| övrúd | – tartó síkjában – tartó síkjára merőlegesen | 0.9 0.9 |
| rácsrúd | – tartó síkjában – tartó síkjára merőlegesen | 0.9 1.0 |
A modell alapú számítógépes eljárásokon alapuló szoftverek (pl. a Consteel szoftver) a fenti konzervatív szabály helyett az Ncr rugalmas kritikus erőt közvetlenül végeselemes numerikus módszerrel, a teljes rácsos tartó viselkedésének figyelembe vételével, határozzák meg. Az alábbi példával a szabvány által javasolt kézi méretezési eljárás és a modern, modell alapú numerikus eljárás eredményének viszonyát kívánjuk szemléltetni.
- Legyen a vizsgált rácsos tartó szerkezeti modellje az 1. ábrán látható Consteel modell.
- A feltűntetett teher feleljen meg a tartó mértékadó tervezési teherkombinációjának.
- Határozzuk meg a legjobban igénybe vett nyomott övrúd kihajlási hosszát végeselemes numerikus stabilitási analízis segítségével.
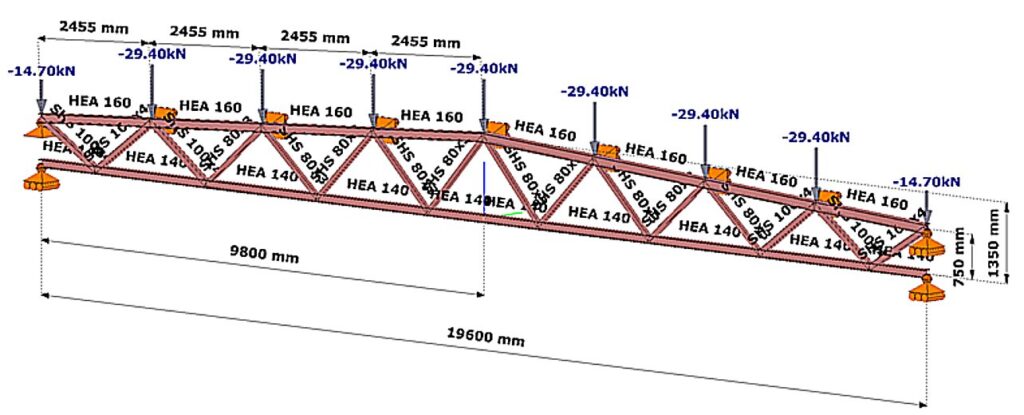
(Consteel szoftver)
Eljárások összehasonlítása
A számítás lépései a következők:
Rugalmas stabilitási analízis
A rugalmas modell stabilitási analízise megmutatja, hogy a rácsos szerkezet mértékadó stabilitásvesztési módját és az ahhoz tartozó αcr rugalmas kritikus teherszorzót (2. ábra).
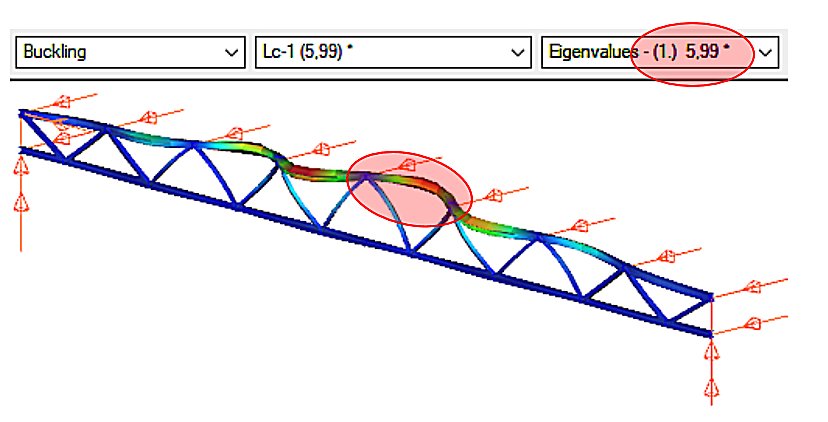
Láthatjuk, hogy a terhelés hatására a tökéletesen rugalmas modell felső öve oldalsó irányban kihajlást szenved. A teher, amely hatására a rugalmas kihajlás bekövetkezik, a kritikus teher, amelynek értékét a tervezési teher és az αcr=5.99 kritikus teherszorzó szorzata adja meg.
gateA nyomott rúd méretezésének fejlődése
A rudakból épített acélszerkezetek (pl. rácsos tartók) egyik jellegzetes alkotó eleme a nyomott rúd. Nyomott rúdról akkor beszélünk, ha a rendszerint egyenes tengelyű szerkezeti elem központos P nyomóerővel terhelt (1. ábra).

A 2. ábra a nyomott rúd méretezésének fejlődését illusztrálja. Kezdetben (a régi időkben) az építőmesterek az évszázadok során felhalmozódott tapasztalati ismeretek alapján, amelyek mesterről tanítványra szálltak, állapították meg a különböző anyagú és méretű nyomott oszlopok teherbírását. Jelentős változást a klasszikus matematikai differenciálanalízis mérnöki alkalmazása hozott. Euler (1707-1783) svájci matematikus és fizikus megoldotta a nyomott rugalmas vonal kihajlásának problémáját, amely megoldás alkalmazható volt a rugalmas nyomott rúd megoldására (Euler erő). A mérnökök a következő évszázadokban felismerték, hogy az Euler erő csak bizonyos esetekben (elsősorban nagy karcsúságoknál) ad elfogadható közelítést a nyomott rúd valós teherbírására. Számos, az Euler képletnél fejlettebb megoldás született a nyomott rúd teherbírására, de jelentős változást csak a II. világháborút követő hatalmas szerkezetépítési konjunktúra hozott. A világ minden számottevő szerkezeti laboratóriumában sorra végezték a nyomott rúd kísérleteket, majd az eredményekből összeállítottak egy több mint kétezer kísérletből álló adatbázist. A nyomott rúd teherbírását az adatbázis alapján, a matematikai statisztika módszerével meghatározott képlettel adták meg.
Ez a módszertan a mai napig meghatározó: „a nyomott rúd méretezése az acélszerkezeti szakma politikai kérdése lett…”. Ezért a nyomott rúd méretezési elvének megértése a szerkezet-építőmérnök számára alapvető fontosságú.
Az ábra jobb oldala a jövőre is tartalmaz utalást. A tudományos kutatás szintjén már jelen, hogy a valós nyomott rúd teherbírását matematikai-mechanikai szimulációval is meg lehet határozni. Sőt, a közeljövőben minden eddigi ismeretet meghaladó adatbázisok hozhatók létre a szuperszámítógépek bevetésével. Egy ilyen gigantikus adatbázis alapján a mesterséges intelligencia felülírhatja az eddigi mérnöki tudást és módszertant, legalábbis elvben. A valóság viszont az, hogy a szerkezet-éptőmérnökség nem tartozik a húzóágazatok közé (mint például a hadipar vagy az autóipar), ezért ez az új méretezéselméleti váltás még egy jó ideig bizonyosan várat magára.

A továbbiakban a ma acélszerkezeti mérnöksége számra kiemelten fontos Euler erőt és a kísérleti alapú szabványos méretezési formulát tárgyaljuk részletesen.
Az ideális nyomott rúd teherbírása: az Euler erő
Tételezzük fel, hogy az alábbi ábrán látható csuklósan megtámasztott nyomott rúd rendelkezik az alábbi tulajdonságokkal:
- tökéletesen egyenes,
- az anyaga tökéletesen lineárisan rugalmas,
- központosan nyomott.
A fenti feltételekkel végezzük el a nyomott rúd kísérletet a Consteel szoftver segítségével: futtassuk a lineáris kihajlási analízis (Linear Buckling Analysis, LBA) számítást. Az eredményt a 3. ábra szemlélteti.
gateThe latest version, Consteel 17 is officially out! In 2023, our main focus for Consteel development is improving usability. New features prioritize efficient model manipulation, easy modification, and clear information presentation across Consteel, Descript, and our cloud-based platform, Steelspace. In this comprehensive video, we walk you through a step-by-step workflow guide, demonstrating how to leverage Consteel 17 to its full potential.
If you would like to delve deeper into the new features, check out our detailed blog post for an in-depth exploration of Consteel 17’s capabilities.
Did you know that you can use Consteel to design simple supported, continuous and over-lapped purlins systems in Consteel, considering shear and rotational stiffness of attached roof sheeting?
To use the purlin design functions, you first need to place cold formed Z or C purlins in your model, these are the only profile types supported for purlin design. All functions related to purlin lines can be found in the Structural members tab.

With these three main functions you can define the purlin line object, specify the support zones, and set the overlap zones. A detailed explanation of each can be found in the Consteel Manual – Purlins Chapter.
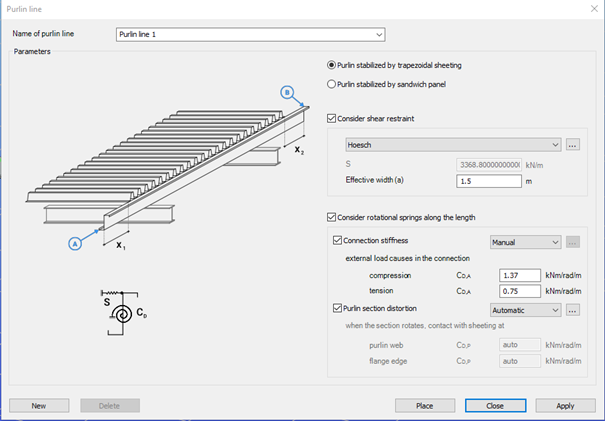
The Place purlin line function allows you to create and configure a purlin line object and place it precisely within your structural model.
You can also control the sheeting eccentricity in the Z direction, either by selecting predefined positions or by entering custom values. A graphical interface supports these settings to ensure intuitive and accurate placement.
An important feature of this function is the ability to simulate the supporting effect of roof sheeting on the purlins. This is done by applying spring stiffnesses that reflect how the sheeting contributes to the overall structural behavior. Two types of springs are considered:
- Translational (shear) spring, representing the shear stiffness of the roof covering.
- Rotational spring, accounting for both the connection stiffness and profile distortion.
Depending on the selected sheeting type (trapezoidal sheeting or sandwich panels) the stiffness values can be entered manually or calculated automatically. Automatic calculations follow the guidelines of EN 1993-1-3, providing reliable and standards-based results.
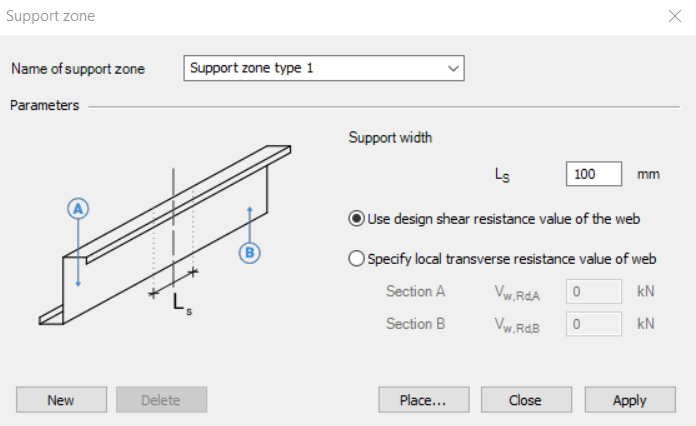
The Support zone function allows you to define the geometrical and mechanical parameters at the points where the purlins are supported. The geometry and bearing capacity can be set by specifying the support width and selecting how the load capacity is defined.
The Purlin overlap function helps define how individual purlins are connected in continuity. The standard (EN 1993-1-3) distinguishes between simple overlap joints and joints with coupling elements. Currently, only overlap joint is available in the program. You can define the length of the overlap either in millimeters or as a percentage of the member length. Additionally, the stiffness distribution between the two overlapping members can be adjusted.
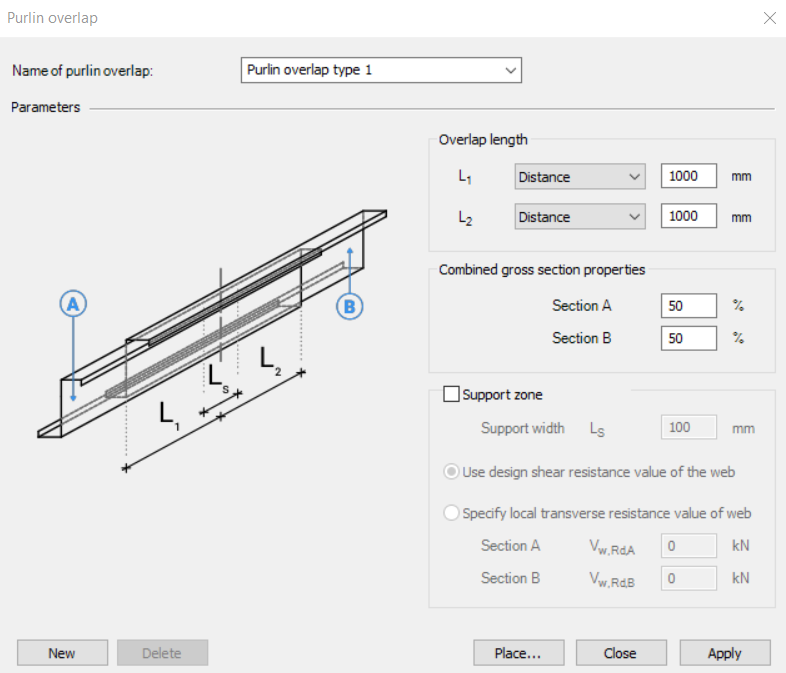
Together, these functions ensure accurate modeling of purlin behavior, support conditions, and connection details, aligning with design standards and practical requirements.
To ensure that all purlin line related objects are properly considered in the analysis, make sure to activate the Cold formed purlin design mode in the analysis settings. When this mode is enabled, both the buckling analysis and the global design are performed on a submodel that includes only those members associated with purlin line objects. This mode is intended exclusively for the design of the roof purlin system.

If purlin related objects are present in the model but the cold formed purlin design mode is not active, the structural elements connected to these objects will be excluded from the second-order stiffness matrix. As a result, their influence will not be considered during linear buckling or second-order analysis.
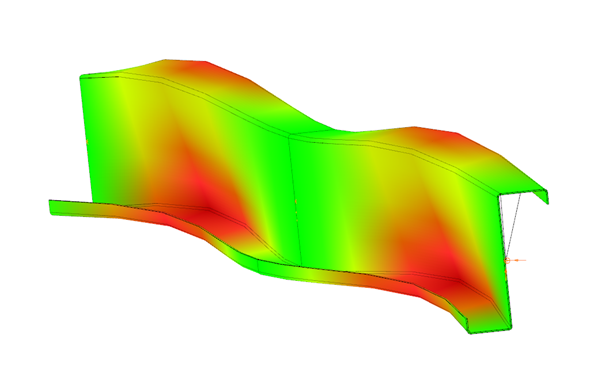
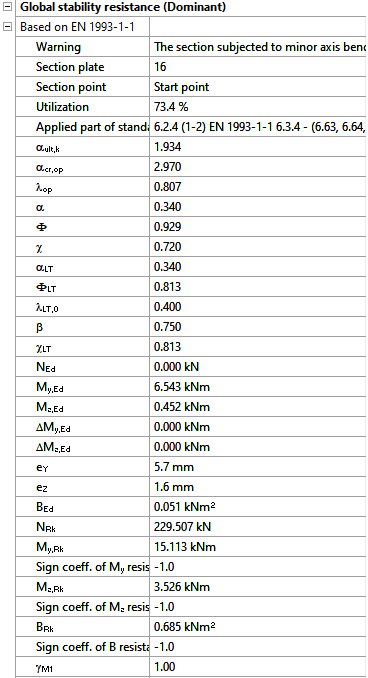
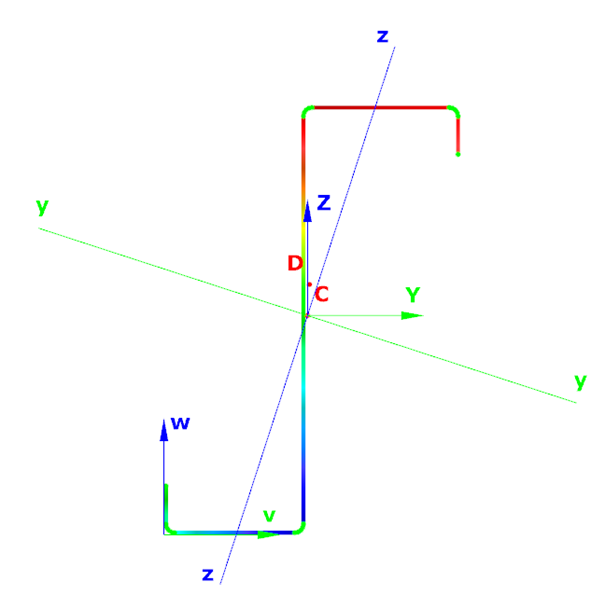
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
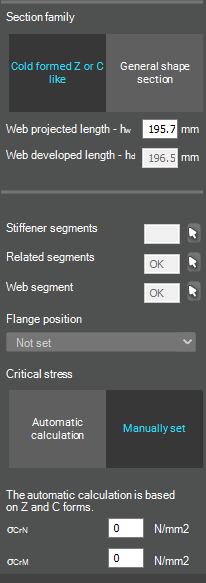
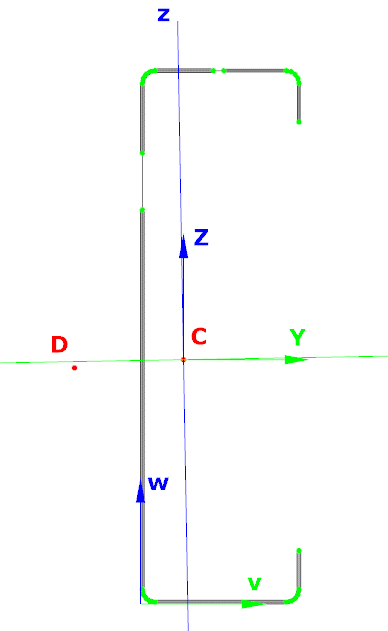
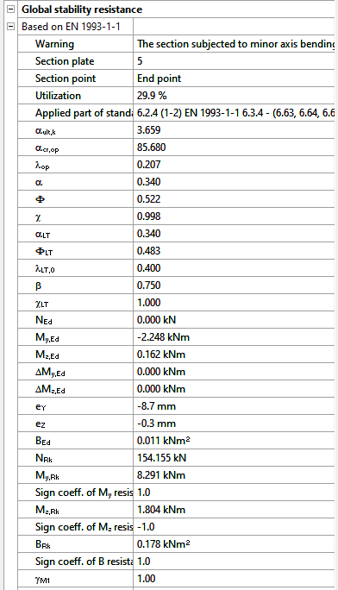
Try Consteel for freeA Consteelben a 3. és 4. osztályú szelvények keresztmetszeti interakciós ellenállása az EN 1993-1-1 6.2 képlet módosított változatával kerül kiszámításra, az öblösödés és a komponens ellenállások előjelhelyes figyelembevételével. Lássuk, hogyan…
GATEDid you know that you could use Consteel to design web-tapered members?
Tapered members are widely used in the economic design of steel-framed structures, such as industrial halls and warehouses, because they make it possible to save material while still ensuring structural strength and stability. With Consteel’s dedicated Tapered Member function, you can model, analyze, and verify these members efficiently, supporting both everyday engineering practice and advanced stability checks.
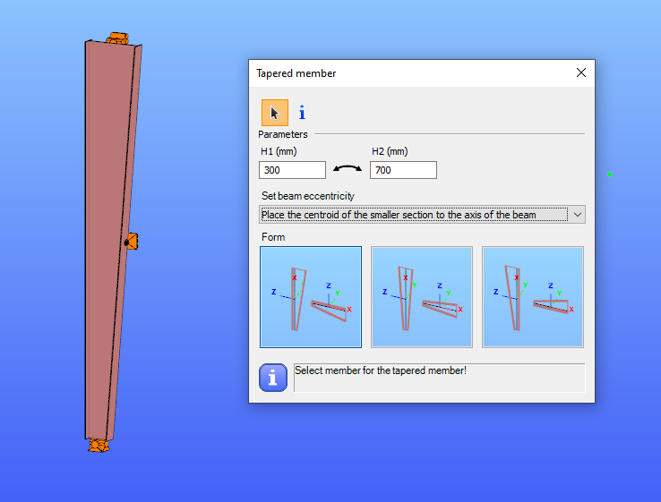
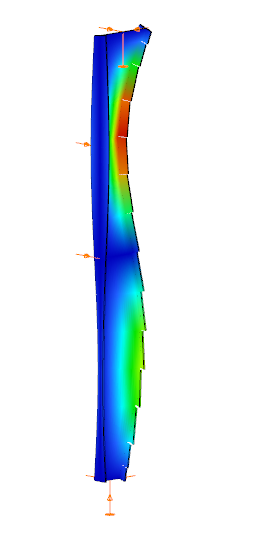
In Consteel, tapered members are line members with welded I or H, box, or cold-formed C sections. Hot-rolled and other macro sections cannot be tapered. Their section height can vary linearly along the member length, making them suitable for realistic structural modeling.
It is best to start with a section close to the smaller end of the taper. The start height (H1) applies at the beginning of the member, and the end height (H2) at the other end. If either value is less than half of the original section height, Consteel automatically resets it to 0.5 times the original. H1 and H2 can be swapped easily with the dedicated icon to reverse the taper direction.
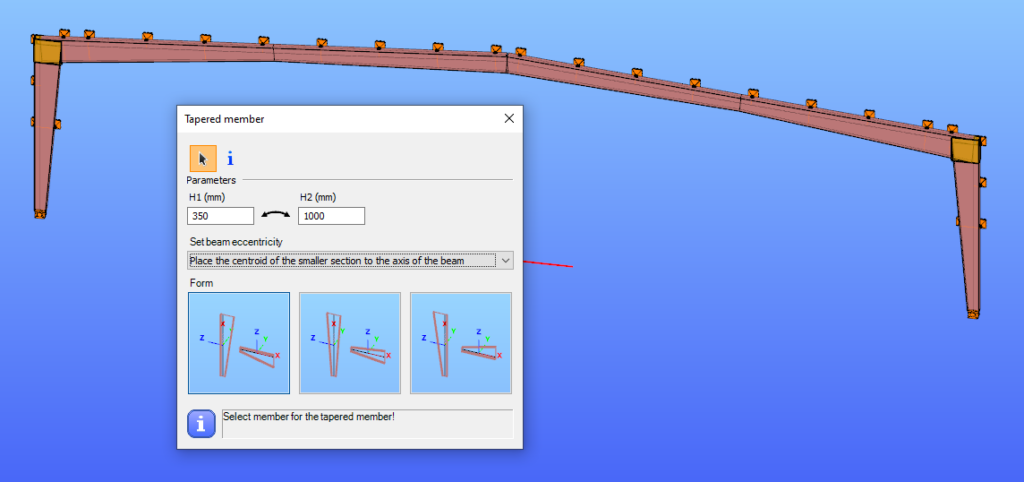
The placement of a tapered member relative to the axis of the original beam is defined by beam eccentricity rules. Consteel offers three alignment options:
- Centroid of the smaller section on the axis – the tapering develops outward from the end with the smaller height.
- Centroid of the larger section on the axis – the bigger end of the member remains fixed to the original axis.
- Centroid of the original section on the axis – one edge of the tapered member coincides with the original section, and the tapering starts from this position.
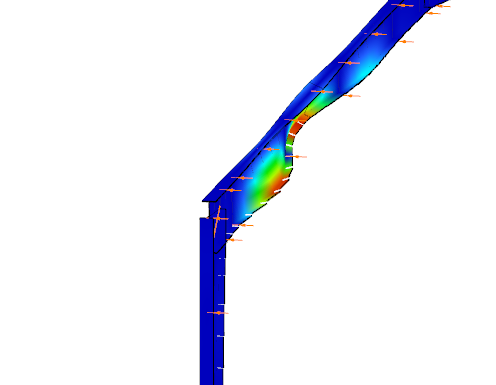
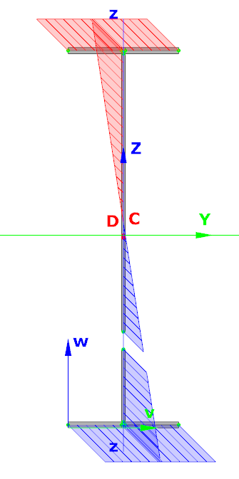
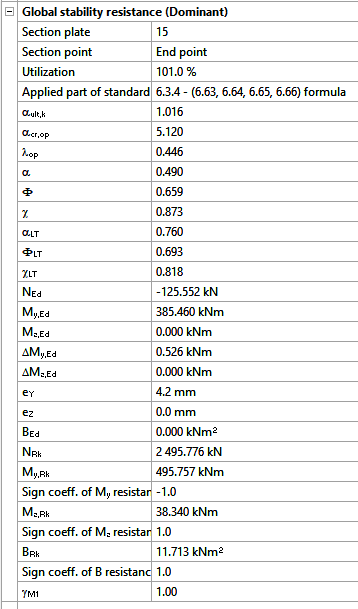
In analysis, Consteel creates tapered sections with the specified start and end heights and places them on the member’s reference line. Unless symmetric tapering is used, this placement is eccentric, which introduces additional effects. At frame joints, for example, extra moments from eccentric axial forces must be considered to maintain equilibrium.
Consteel handles these effects automatically, ensuring realistic results. Symmetric tapering keeps the analysis simpler, while eccentric tapering requires more attention. In all cases, global stability checks should complement sectional verifications to guarantee structural safety.
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for freeDid you know that you could use Consteel to determine automatically the second order moment effects for slender reinforced concrete columns?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free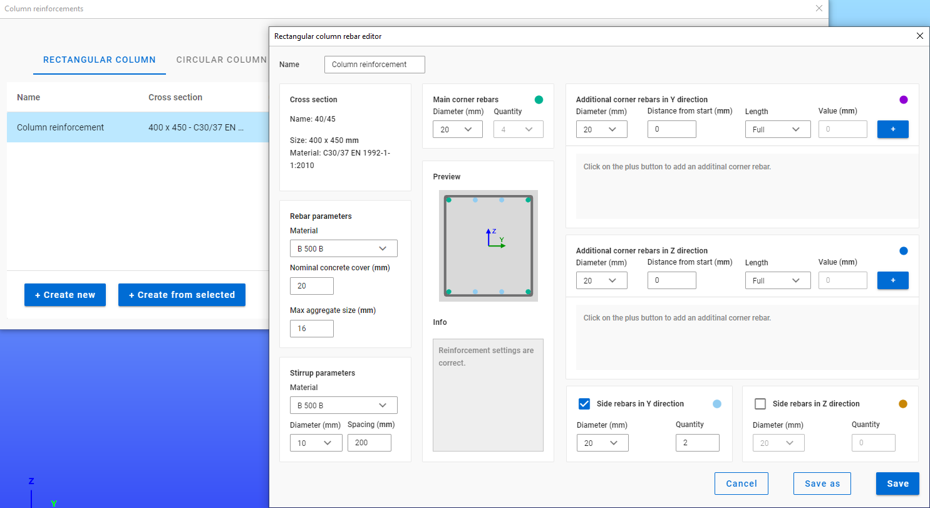
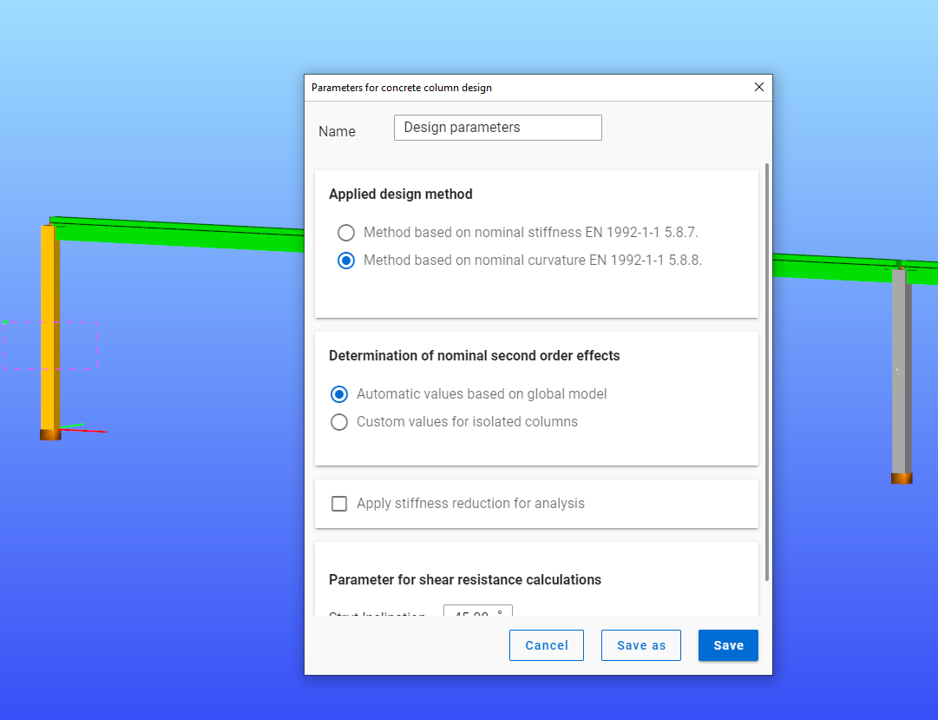
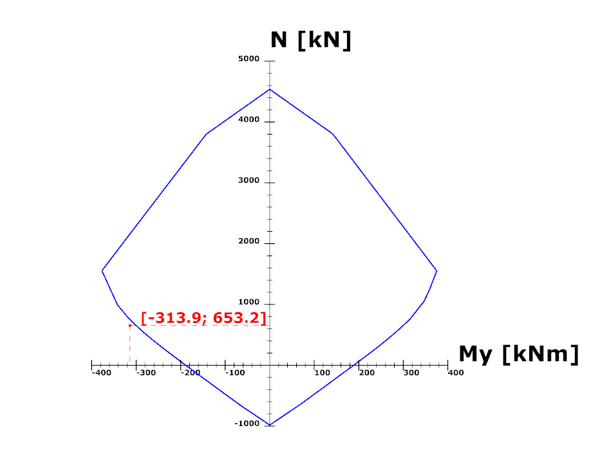
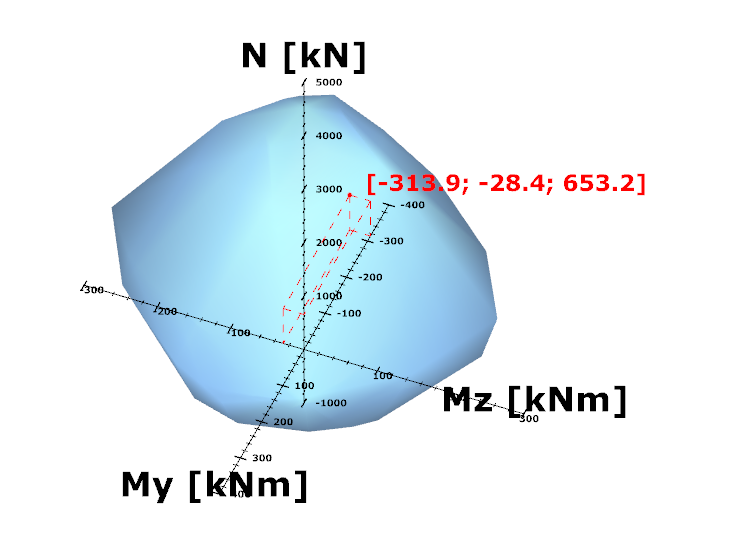
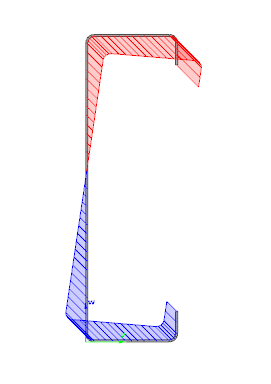
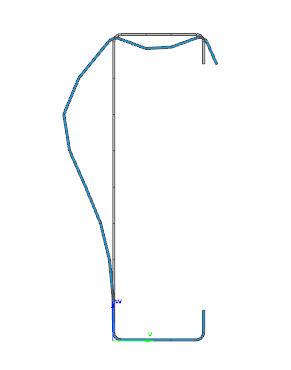
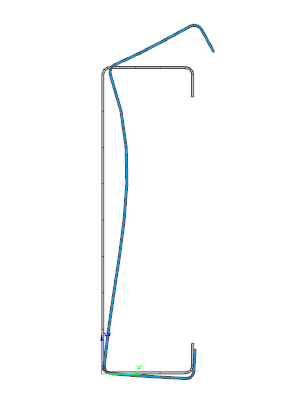
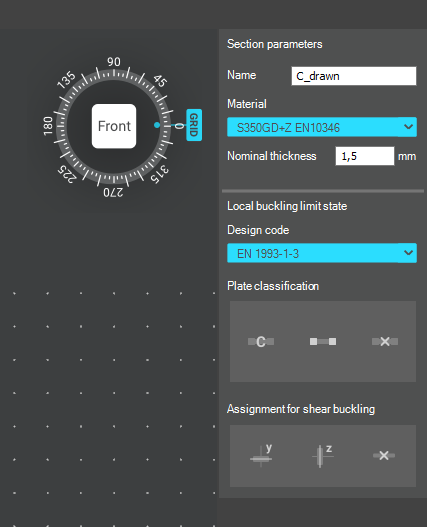
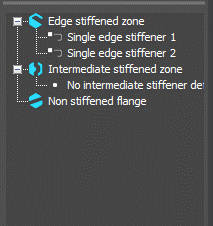
Did you know that you could use Consteel to perform local and distortional buckling checks for cold-formed members?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free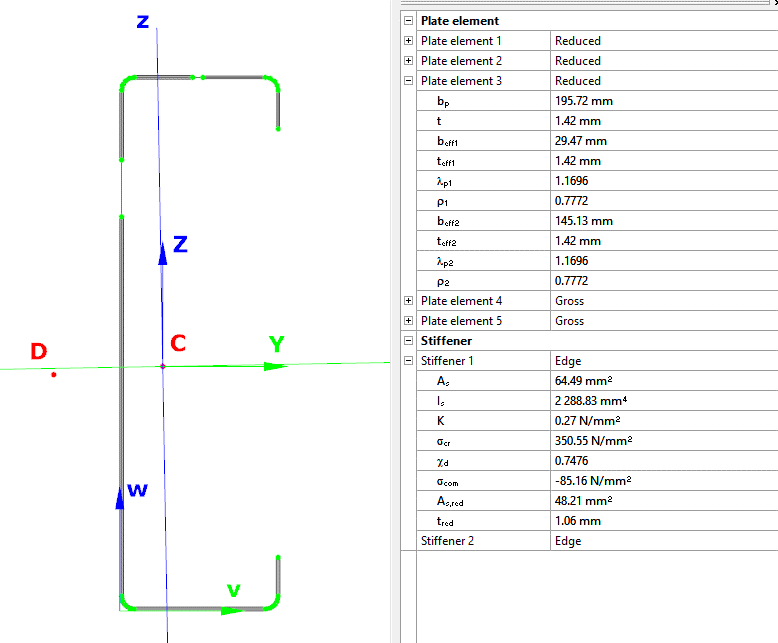
Bevezetés
A vasbeton oszlopok az építőipar alapvető szerkezeti elemei. Előfordulnak például keretvázas épületekben, csarnokokban, családi házakban, de hidaknál is. Alkalmazzák mind monolit, mind előregyártott változatban is.
A tervező célja biztonságos és gazdaságos szerkezetek tervezése. A technológia fejlődésével építőanyagaink is változnak, egyre jobb minőségű betonokat lehet előállítani kedvező költségek mellett. Ennek következtében előnyössé válhat kisebb keresztmetszetű oszlopok alkalmazása.
Ahogy az oszlopok karcsúbbak lesznek, előtérbe kerülnek a stabilitási kérdések és a másodrendű igénybevételek számítása. A ConSteel végeselemes program acélszerkezetekre van specializálódva, ebből kifolyólag pedig gyors és jól automatizált megoldásai vannak stabilitási problémákra.
Kihasználva a szoftverben meglévő lehetőségeket, a ConSteel szoftver 16-os verziójában elérhetővé vált a vasbeton oszlopok tervezésére egy újfajta, ConSteel által továbbfejlesztett módszer alkalmazása. Ez az Eurocode 5.8.8 [1] -ben leírt Névleges görbület módszeren alapszik.
A Névleges görbület módszere alkalmazásához sok információt kell megadni, különféle anyagi-és geometriai paramétereket. A dokumentum célja bemutatni, hogy a ConSteel 16-ban kiterjesztett Névleges görbület módszer választ ad az összes tervezés közben felmerülő kérdésre, és mentes az eredeti módszer több hiányosságától is.
Az Eurocode 2 áttekintése – vasbeton oszlopok tervezése
Ebben a fejezetben az Eurocode 2, Névleges görbület módszerén alapuló vasbeton oszlopok tervezését mutatjuk be nagyvonalakban, összpontosítva a hangsúlyosabb részekre.
Anyagi paraméterek
Parciális biztonsági tényezők:
- Beton rugalmassági modulusa
?cE = 1.20 - Beton
?c = 1.50 - Acélbetét
?s = 1.15
A beton anyagi tulajdonságaival az Eurocode 1992-1-1 3.1. fejezete foglalkozik.
Rugalmassági modulus:
- Tervezési érték
- ?cd = ?cm/γcE
- A várható érték csökkentése γcE biztonsági tényezővel
- Teherbírási vizsgálat esetén alkalmazandó
- Abban az esetben, ha a kúszást nem kell figyelembe venni, vagy máshol vesszük figyelembe
- ?cd = ?cm/γcE
Kúszás
A kúszási tényező számításáról az EN 1992-1-1 3.1.4 fejezet beszél. Itt különböző tényezők segítségével meg lehet határozni a kúszási tényező végértékét, betonszilárdság függvényében, diagramok segítségével. Az értékek meghatározhatóak az EN 1992-1-1 B Melléklete szerint is. A két számítás közel azonos eredményhez vezet.
Imperfekciók
Az imperfekciók figyelembevételét az Eurocode 1992-1-1 5.2-es fejezete taglalja. Az imperfekciók figyelembevételét alapvetően két részre bontja. Az egyik a globális ferdeség, ez látható a 1. ábra b) részén. A másik rész amikor a hálózati pontok nem mozdulnak el, de közte az elemek görbültek. Ez a kezdeti görbület (vagy más néven alakhiba), a 1. ábra c) része szemlélteti.

Ferdeség
A ferdeségből származó imperfekció hatását figyelembe lehet venni fiktív keresztirányú erők számításával. Ehhez az alkalmazott ferdeség értékét a következőképpen kell számolni:
- ferdeség alapértéke
θ0 = 1/200 - magasságtól függő csökkentő tényező
αh = 2/√?
ahol ? a magasság - szerkezeti elemek számától függő csökkentő tényező
αm = √0.5(1 + 1/?)
?: teljes hatás felvételében szerepet játszó függőleges szerkezeti elemek száma - alkalmazott ferdeség
θi = θ0αhαm
Ezek után az 2. ábrán látható módon az normálerőkből merevítetlen estben a fiktív keresztirányú erők számolhatóak: ?i = θi? módon..
Merevített esetben, például egy csuklós-csuklós oszlopnál a ?i erőt nem a rúd tetőpontjába, hanem a rúd középpontjába kell definiálni, és nagysága: ?i = 2θi?.
![Isolated member with eccentric axial force or lateral force. Unbraced (left) and braced (right) - EN 1992-1-1 Figure 5.1(a) [1]](https://consteelsoftware.com/wp-content/uploads/2023/06/2_isolated-member-with-eccentric-axial-force-or-lateral-force.png)
Másodrendű hatások
Az EN 1992-1-1 szabvány 5.8.8 fejezetében bemutatott módszer alapértelmezés szerint elkülönített, állandó keresztmetszetű és konstans normálerővel terhelt oszlopokra alkalmazható.
A méretezési módszer az oszlop másodrendű hatások következtében legnagyobb görbületet szenvedő pontjában egy maximálisan elképzelhető határgörbület segítségével meghatározott maximális másodrendű nyomatékot (?2) eredményez, aminek a hossz menti lefutását közvetlenül nem határozza meg. A biztonság és egyszerűség szempontjából szokás ezt a nyomatékot egyenletesen feltételezni a hossz mentén, de a szabvány megengedi a szinuszos vagy a parabola-szerű lefutást is.
Görbületeloszlásra vonatkozó reális feltételezések esetén az Eurocode megengedi a módszer használatát teljes szerkezetek esetén is (EN 1992-1-1 5.8.5 (3)), azonban ez kézi módszerek esetén általában nem lehetséges, az egyes elemek közötti interakciók miatt.
A módszer használatához elengedhetetlen a kihajlási hossz megadása, a másodrendű nyomaték nagysága függ tőle. Ehhez a szabvány megengedi a rugalmas elmélet során alkalmazott tényezők használatát (konzol esetén ?0 = 2?, alul befogott – felül megtámasztott esetben ?0 = 0.7?, stb.).
A hajlítónyomaték számítása:
?Ed = ?0Ed + ?2
ahol
?0Ed elsőrendű nyomaték, amely tartalmazza a méreteltérések (imperfekciók) hatását
?2 névleges másodrendű nyomaték (tartalmazza mindennemű görbület hatását).
Görbületből származó másodrendű nyomaték számítása
A másodrendű nyomaték számításához először a névleges görbületet kell meghatározni:
1/? = ?r?φ1/?0
ahol
- ?r normálerőtől függő csökkentő tényező
- ?φ kúszás hatását figyelembe vevő növelő tényező
- 1/?0 tönkremenetelhez tartozó elméleti (fizikai) görbület
1/?0 = ε??/0,45?
A görbület ahhoz a ponthoz tartozik, amikor a beton eléri a határösszenyomódását ( ε?? ) és a húzott betonacél éppen megfolyik, vagyis az úgynevezett „kiegyensúlyozott” eset.
Azt, hogy a teherbírási vonal melyik részén vagyunk a normálerőtől függő csökkentő tényező veszi figyelembe:
?r = (?u − ?)/(?u − ?bal)
ahol
- ? = ?Ed / Ac?cd
fajlagos normálerő
- ?Ed
normálerő tervezési értéke
- ?Ed
- ?u=1+ω
- ω = As?yd / Ac?cd
mechanikai vashányad - As
betonacélok teljes keresztmetszeti területe - Ac
betonkeresztmetszet teljes területe (külső befoglaló méret)
- ω = As?yd / Ac?cd
- ?bal =0.4
n értéke a legnagyobb nyomatéki teherbírásnál - (0.4 alkalmazható bővebb információ hiányában)
A kúszást figyelembe vevő csökkentő tényező:
?φ = 1 + βφef ≥ 1
ahol
- φef = φ(∞,0) ?0Eqp / ?0Ed
hatékony kúszási tényező
- ?0Eqp elsőrendű hajlítónyomaték kváziállandó (használhatósági határállapot) kombináció alapján
- ?0Ed elsőrendű hajlítónyomaték (teherbírási határállapotnak megfelelő) tervezési kombináció alapján
- ?0Eqp elsőrendű hajlítónyomaték kváziállandó (használhatósági határállapot) kombináció alapján
- β=0,35 + ?ck/200−λ/150
- λ = ?0 / ?
karcsúság - ?0
kihajlási hossz - i = √?c/?c
repedésmentes betonkeresztmetszet inerciasugara
- λ = ?0 / ?
A másodrendű nyomaték
?2=?Ed?2
ahol

másodrendű külpontosság, ahol c a görbületeloszlástól függő tényező. Állandó keresztmetszet esetén ?=?2 használható. Ez szinusz alakú görbületeloszlásnak felel meg. Állandó görbület esetén ?=8 használható.
Méretezés
Teherbírási vonal
A teherbírási vonal értelmében a vasbeton oszlop nyomás-hajlítás interakciója során a tönkremenetel mindig akkor következik be, amikor a beton eléri az alakváltozási kapacitását (általában ?cd = 0,35%).
Ebben a pillanatban attól függően hol vagyunk a teherbírási görbén, a másik oldali acélbetét:
- húzott és már egy ideje folyik,
- húzott és éppen megfolyik,
- húzott, de rugalmas
- nyomott és rugalmas
A továbbfejlesztés elméleti háttere
A méretezési eljárás a 2. fejezetben ismertetett szabványos eljárás kiterjesztése. A kihajlási hosszok kézi megadását automatizálja, illetve megadja a másodrendű igénybevételek lefutását.
A számítás alapját szolgáló görbületeloszlás kiinduló értékét a globális szerkezeten végzi és nem egy elkülönített oszlopon. A görbületeloszlást a teljes szerkezeten számolt rugalmas kihajlási alakokból kiindulva határozza meg (Lineáris kihajlásvizsgálat – LBA).
Ez egy reális görbület eloszlásnak tekinthető a szerkezetre nézve, mert a teljes szerkezetre számolunk kihajlási alakokat, így figyelembe vesszük a szerkezetei elemek kölcsönhatását is. Ezzel a módszer kiterjeszthető, az oszlop már nemcsak elkülönített elemként, hanem a teljes szerkezet egy részeként lesz vizsgálható az Eurocode értelmében (EN 1992-1-1 5.8.5 (3)).
A végső lépést, a másodrendű nyomatékok (?2), meghatározását már elkülönített modellen végzi a szabvány szellemében, de ehhez a görbületi alaknak felhasználja a teljes modellen számított megfelelő kihajlási alaknak az adott oszlop mentén kapott értékeit.
A kihajlási alak maximum értékét a szabvány által előírt görbületre (1/?) nagyítja, a többi értéket pedig ezzel arányosan változtatja.
A megfelelő sajátalak hozzárendelést egy Kihajlás-érzékenység vizsgálat nevű eljárás végzi. A nagyítást a sajátalak oszlop hossza mentén talált legnagyobb görbületi pontjában végzi el.
Ezzel a módszerrel elméletileg bármilyen szerkezeti elemre és a teljes szerkezetre képesek lennénk másodrendű nyomatékok számítására. Jelen fejlesztési fázisban azonban még csak vasbeton oszlopként definiált, egyenes tengelyű rúdelemeknél vesszük figyelembe.
Később, amennyiben igény mutatkozik rá, megfelelő tesztelés és verifikálás után, általános érvényűvé fejleszthető az eljárás. Ez igen hasznos funkció lehetne például vasbeton ívek, vagy nyomatékbíróan vasalt vasbeton keretállások esetén.
Kihajlás-érzékenység vizsgálat
A módszernél a legnagyobb nehézség, hogy egyes rúdelemeknek legyen mértékadó kihajlási alakja mindkét irányban (ha z a függőleges, akkor x és y irányban). A szerkezetnek a felhasználó által meghatározott számú sajátalakja kerül meghatározásra.
Minden egyes alakot, mint elmozdult alakot feltételezvén a szerkezet minden rúdeleme mentén kiszámoljuk rúdelemenként az összegzett deformációs energiát.
Az éppen vizsgált kihajlási hossz alapján számított legnagyobb deformációs energia értéket mutató elemhez 100% értéket rendelünk, a többi elemhez arányosított értéket. Az éppen vizsgált kihajlási alakot az annak megfelelő rúdelemhez rendelünk.
Mivel egy oszlop általánosságban a két merőleges irányban is kihajolhat, a vizsgálatot mindkét lokális irányban elvégezzük és egyetlen oszlophoz 2 sajátalakot rendelünk (irányonként 1-1).
Másodrendű nyomaték meghatározása
Az Eurocode szerint:
?2 = ?Ed?2

ahol ? = π2
A ConSteel hasonlóképpen számol. A vasbeton oszlop minden végeseleméhez számolunk másodrendű nyomatékot. Ehhez három értéket használunk fel. Az első a végeselem pontban a normáligénybevétel (?Ed). A második az Eurocode szerint meghatározott másodrendű külpontosság (?2).
Ezek után a harmadik érték az adott végeselem pontban a kihajlási alak ordinátája, úgy, hogy a kihajlási alak maximumát egységnyire normáltuk. Ezzel a harmadik értékkel felszorozva az első kettőt kapjuk meg a vasbeton oszlop adott végeselem pontjában a másodrendű nyomatékot. Ez egy pontosított nyomatéki eloszlást eredményez.
Különbségek a szabványos eljáráshoz képest
Egyszerűsítés a hatékony kúszás számításánál:
φef = φ(∞,?0)
konzervatív módon a hatékony kúszást egyenlővé tesszük a kúszási tényező végértékével, csökkentés nélkül. Ezzel elkerülve olyan hibákat, mint például, ha kváziállandó teherkombinációban nincs nyomaték, akkor a hatékony kúszási tényező értéke definíció szerint zérus.
Kúszási tényező értéke ConSteelben
A ConSteel-ben szereplő értékek a Vasbeton Szerkezetek Eurocode segédlet [6] 1. Táblázatából származnak.
Ez az EN 1992-1-1 3.1.4 fejezetét veszi alapul. Itt különböző tényezők segítségével meg lehet határozni a kúszási tényező végértékét, betonszilárdság függvényében, diagramok segítségével.
Karcsúság számítása kihajlás-vizsgálat alapján

Euler rúd kritikus ereje. A képletet átrendezve:

ahol

Nincs szükség a kihajlási hossz megadására, a karcsúság számítása automatizált.
Másodrendű nyomaték eloszlása kihajlási alak alapján
A másodrendű nyomaték eloszlása megegyezik a kihajlási alakéval, ezzel figyelembe véve az oszlopok közötti interakció is.
A módszer bemutatása konzolos példán keresztül
A modell létrehozásához szükséges információkat a Vasbeton oszlopok tervezése – Áttekintés című cikkünkben találod.
Vagy töltsd le a modellcsomagot a cikk végén található gombra kattintva és nyisd meg a „separate_circle_column_cantilever.csm” fájlt.
Elsőrendű analízis
Elmozdult alak: az értékek reálisnak tűnnek:
- kis mértékű függőleges elmozdulás
- abban az irányban, ahol nagyobb vízszintes terhet tettünk rá nagyobb elmozdulás
- másik irányban a rárakott imperfekció miatt kis elmozdulás
- az elmozdult alak a vártnak megfelelően a vízszintes teher irányában görbült
Ezután érdemes ellenőrizni az igénybevételeket

N
- függőleges teher értéke végig (nincs önsúly most)
negatív előjel -> nyomás
Vy+Mz
- normálerőből számoluk az imperfekciót
- 675*0,005 = 3,375 kN
- 3,38*3 = 10,14 kNm
- az alakok és az értékek is stimmelnek
- igénybevételből nincs Vy+Mz, csak imperfekcióból


Vz +My
- normálerőből számolunk az imperfekciót
- 675*0,005 = 3,375 kN
- 3,38*3 = 10,14 kNm
- Ezek az imperfekcióból számolt igénybevételek
- plusz hozzájön 20*1,5 = 30 kN teher
- 30+3,375 = 33,375 kNm
- 33,375*3 = 100,125 kNm
- ezek az igénybevételek is stimmelnek,
- elsőrendű igénybevétel terhekből + ferdeség


Kihajlás számítás és Kihajlás érzékenység

A koordinátákból látható, hogy síkbeli kihajlási esetről van szó.
Egy oszlop esetén viszonylag könnyű ellenőrizni, hogy van-e mindkét irányban mértékadó sajátalak. Itt most csak egy darabot sikerült számolni, úgyhogy biztos nincs.

Módosítani kell a kihajlásszámítás paramétereit. Érdemes növelni a releváns kihajlási sajátértékek felső határértékét, illetve a számolt kihajlási alakok számát.
Töltsd le a cikk végén található modellcsomagot és nyisd meg a módosított „separate_circle_column_cantilever_MoreBucklingShape.csm” modellfájlt.
Több kihajlási alakot számítva már van mindkét irányban.


Teherbírás számítás – EN 1992 szerinti feltétel
Most minden szimmetrikus.
GATE



