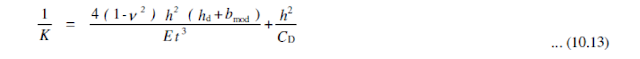Did you know that you could use Consteel to perform local and distortional buckling checks for cold-formed members?
First, sections must be loaded into the model. To load cold-formed sections, you can choose from four options: From library, Macro section, Draw section, or My library.
After the first-order and buckling analyses are completed, you can proceed to the Ultimate limit state check settings and enable the steel design cross-section and buckling checks. At the bottom of the steel design section, there is an option to Consider the supplementary rules from EN 1993-1-3 for the design of cold-formed sections. This checkbox must be selected if you want to design cold-formed sections.
When the calculation is finished, by opening the Section module, we can review all the properties of the Effective section of the elastic plate segment model. By opening each plate element, we can verify the length, effective length, thickness, effective thickness, slenderness, and reduction factor separately. In addition, the properties of the stiffeners can also be verified: area, moment of inertia, lateral spring stiffness, critical stress, reduction factor, compressive stress, reduced effective area, and reduced thickness.
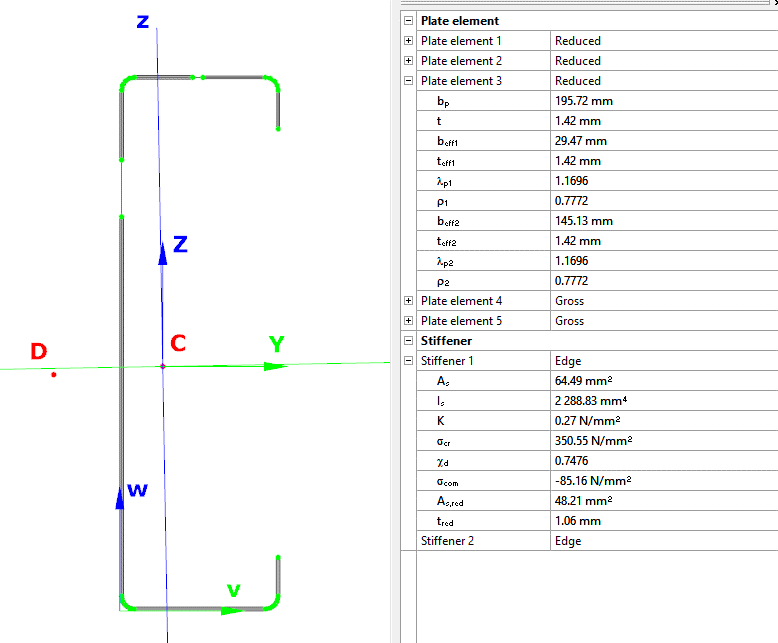
Similarly, the stresses can also be checked from the Properties tab. In the colored figure or diagram view, all the calculated stresses can be seen together with their resultants.
Consteel automatically takes into account the effect of distortional buckling when calculating the effective sections of cold-formed thin-walled sections.
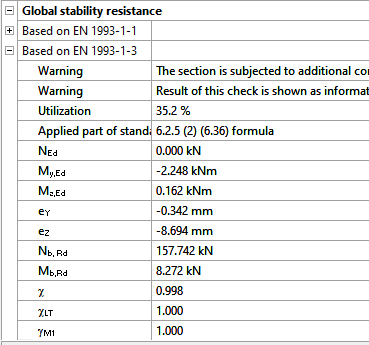
Moving on to the Standard resistance tab in the Section module, all calculated results can be verified, not only the dominant one. By opening the Global stability resistance check, we can see that, since we enabled the option to consider the supplementary rules from EN 1993-1-3 for the design of cold-formed sections, results are available both according to EN 1993-1-1 and according to EN 1993-1-3.
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for freeEN 1993-1-3 contains 3 „secret” formulas. The first two are used to determine the effective cross section due to distortional buckling when edge or intermediate stiffeners are involved. The third is used to calculate the distortion of the whole cross section when analyzed with a connected sheeting.
The physical meaning of all three formulas can be easily shown with simple ConSteel models which helps designer to understand the underlaying mechanial model.
The first formula (5.10) is used when the ability of an edge stiffener to stabilize a compressed flange of Z or C section is studied. During distortional buckling the intersection point of flange with the lip (it is called as edge stiffener) is expected to move in a direction perpendicular to the flange. This formula gives the stiffness value provided by the Z or C section, when is assumed that during deformations the point of intersection of the web with the flange doesn’t move. This assumption corresponds to attaching supports to these nodes as seen on picture 5.6 of EN 1993-1-3.
When a compressed edge stiffener would buckle, it will be partially restrained by the section with these attached supports. Depending on the distribution of normal stresses on the section, one or two edge stiffeners might be under compression. If both stiffeners are under compression and tend to buckle, the restraining capacity of the section will have to be shared between them. This sharing requirement is reflected by the coefficent kf. The spring stiffness value will be used as a distributed spring support when the buckling resistance of the edge stiffener is calculated.
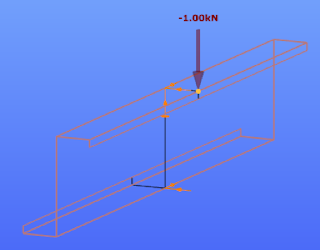
Stiffness values are typically calculated as the ratio of a displacements obtained from the application of a unit load. In this case the unit loads are applied parallelly to the expected displacement of the compressed edge stiffeners.
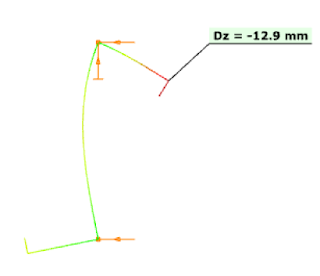
The ConSteel model shown below reproduces the stiffness calculation for a 1 m long Zee section (as a simplification the unit loads are placed at the intersection of the flange with the lip and not at the center of the gravity of the edge zone):
Z purlin, nominal thickness = 1.30 mm, 200 mm deep, 72 mm wide symmetric flanges, 15.5 mm deep lips
in case of My bending: kf = 0, b1 = b2 = 72 mm, hw = 198.7 mm, t = 1.26 mm
K1 = 210000*1.26^3/4*(1-0.3^2)*1/(72^2*198.7+72^3+0.5*72*72*198.7*1.0) = 0.08 N/mm2
The resulting vertical displacement from the point load is 12.9 mm.
gate