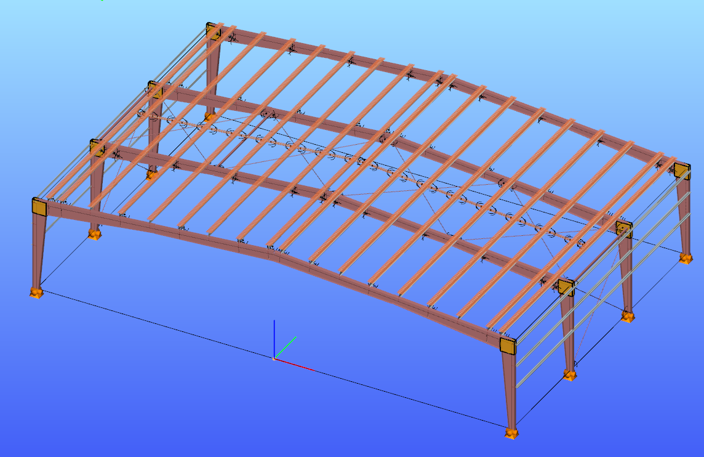
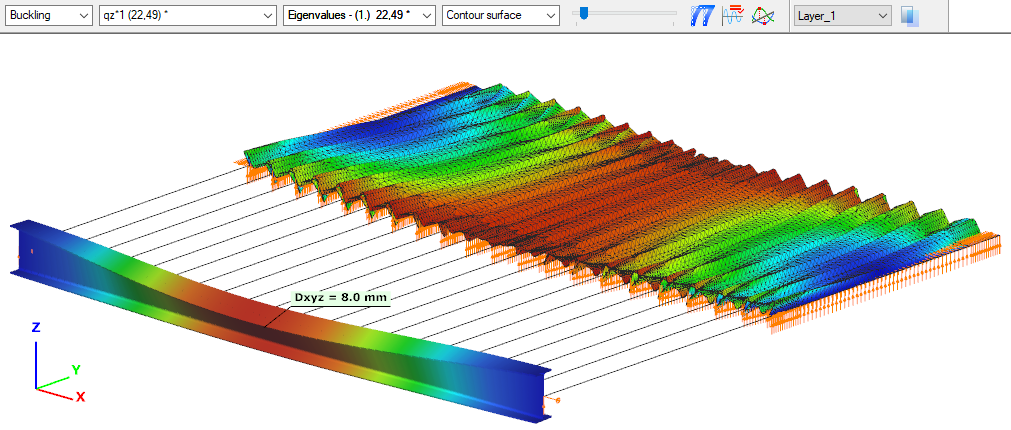
Did you know that you could use Consteel to Consider the shear stiffness of a steel deck as stabilization for steel members?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free

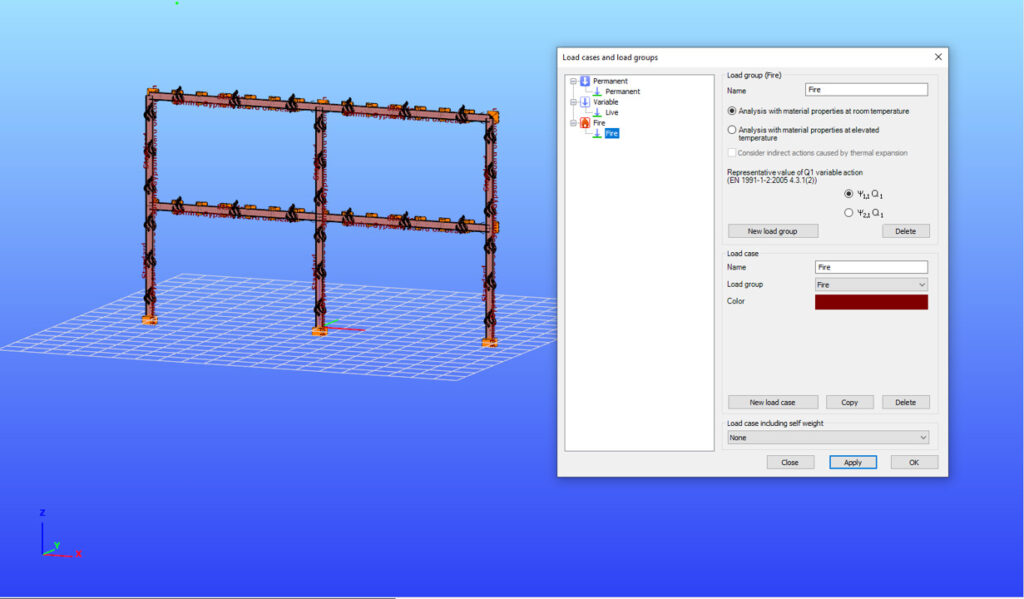
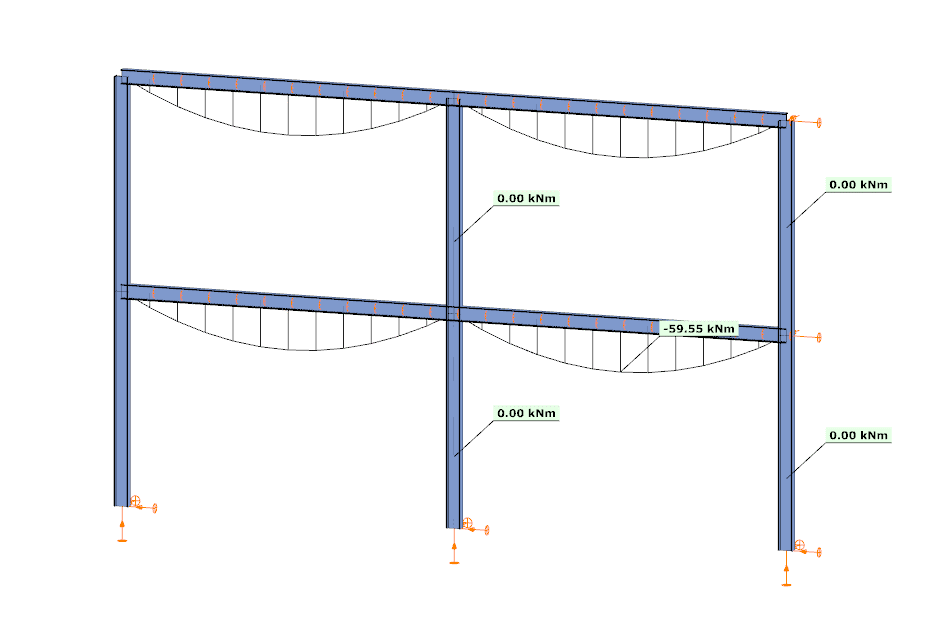
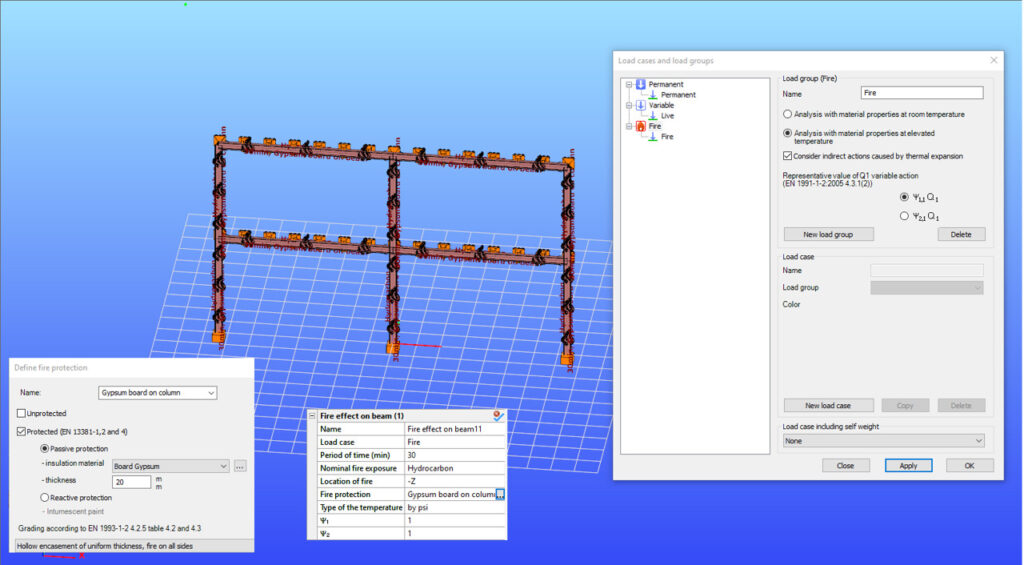
Did you know that you could use Consteel to perform structural analysis at room and elevated temperatures as part of design process for fire resistance?
Download the example model and try it!
Download modelsIf you haven’t tried Consteel yet, request a trial for free!
Did you know that you could use Consteel to calculate the elastic critical moment of a member subject to arbitrary loading and boundary conditions?
Calculating the elastic critical moment can quickly become difficult when beams have tapering, unusual restraints, or complex loads. Consteel simplifies the process and gives a quick, accurate result for any situation.
The elastic critical moment for lateral-torsional buckling is the theoretical bending moment at which a beam, free to sway sideways and twist, becomes unstable and buckles elastically, before yielding, representing the absolute upper limit of elastic stability for beam bending. It depends on: cross-section stiffness properties (Iz, Iw), material (E, G), span / buckling length, restraint to lateral displacement and to warping at the restraints, and on the shape of the moment diagram (via factors C1, C2, C3).
For doubly symmetric I- or H-sections with constant cross-section, uniform bending, and classical boundary conditions, the elastic critical moment Mcr can be calculated using the analytical formula:
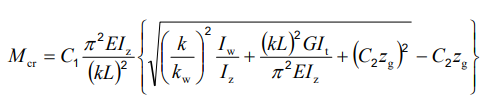
However, for arbitrary support conditions and loading scenarios, the calculation becomes significantly more complex, and the classical formula is no longer applicable. In such cases, specialized software such as LTBeam or Consteel is required.
Let’s consider a tapered, welded I-section with pinned supports at both ends and two intermediate restraints, one at the bottom flange and one at the top flange. In addition to the uniform distributed load, a bending moment is applied at one end of the beam.
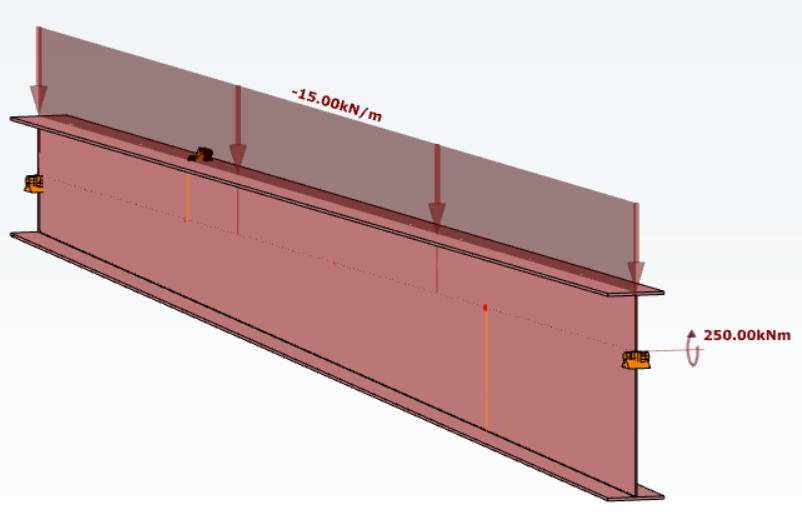
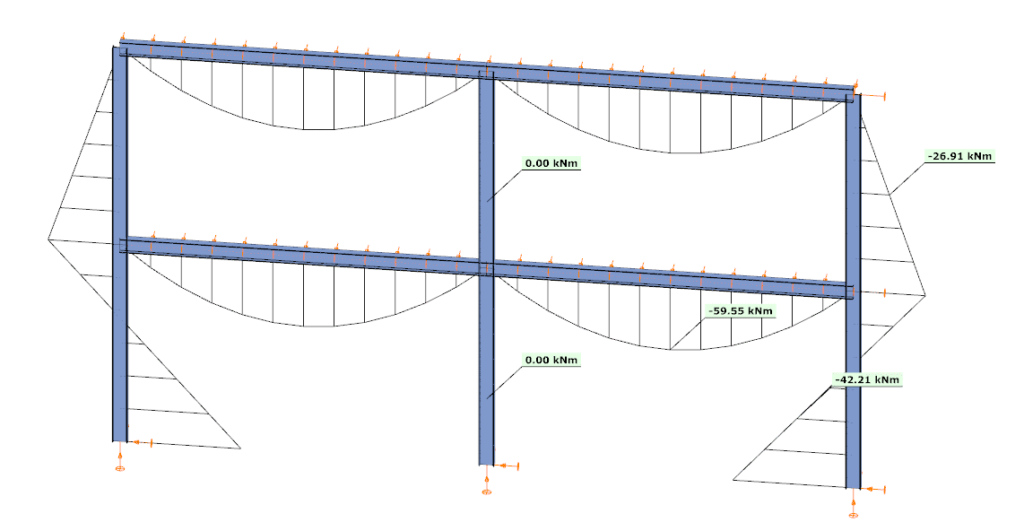
By performing a buckling analysis in the Analysis tab, the buckling shapes and the critical load factor (αcr) can be obtained. The elastic critical bending moment of the beam can be then calculated by multiplying the critical load factor by the maximum bending moment.
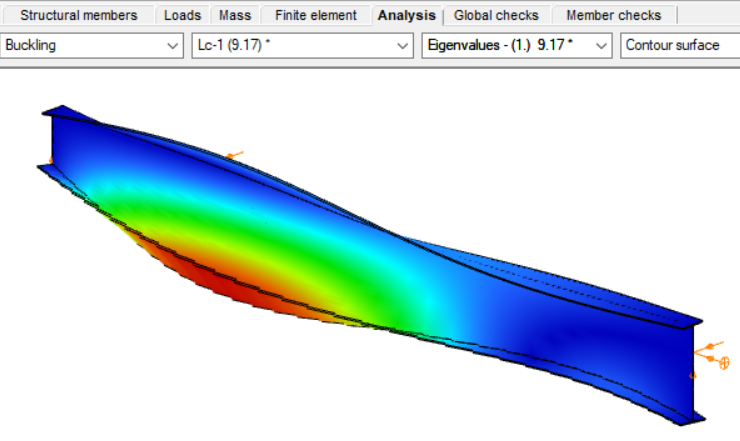
Consteel uses seven-degree-of-freedom finite element that fully accounts for tapering effects, torsion, and warping, key components in accurately capturing the true 3D behaviour of steel members. The seventh degree of freedom represents cross-sectional warping, which becomes visible in the buckling shape as the flanges move out of the plane of the cross-section.
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for freeA Consteel lehetőségek széles skáláját kínálja a teherkombinációk szűréséhez, amely határállapot, tehereset, valamint analízis eredmények és kihasználtságok alapján is történhet. Szűrők különböző kombinációinak alkalmazásával a tervezési folyamat tudatosabbá válhat és csökkenhet a számítási idő.
Szűrési lehetőségek
A szűrést a Teherkombináció csomag megadása nevű dialóg on lehet elvégezni.
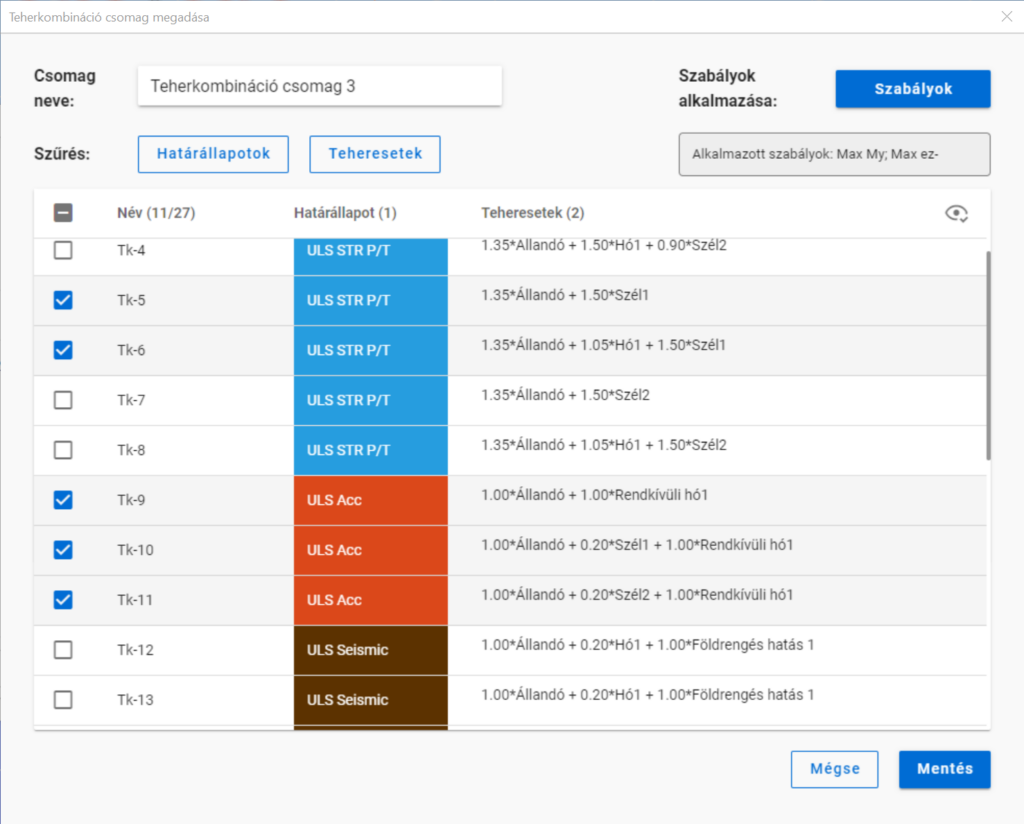
A határállapotok és teheresetek szerinti szűrést az azonos nevű gombok alatt lenyíló jelölőnégyzetekkel lehet végrehajtani.
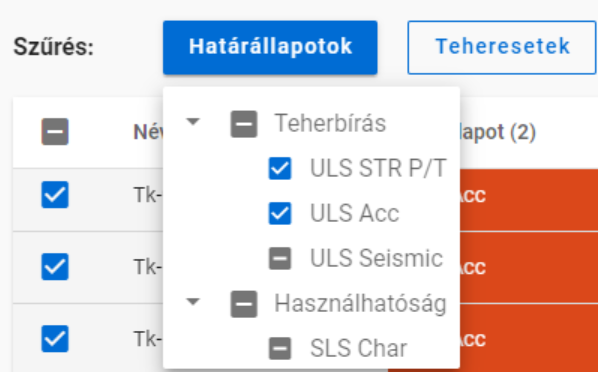
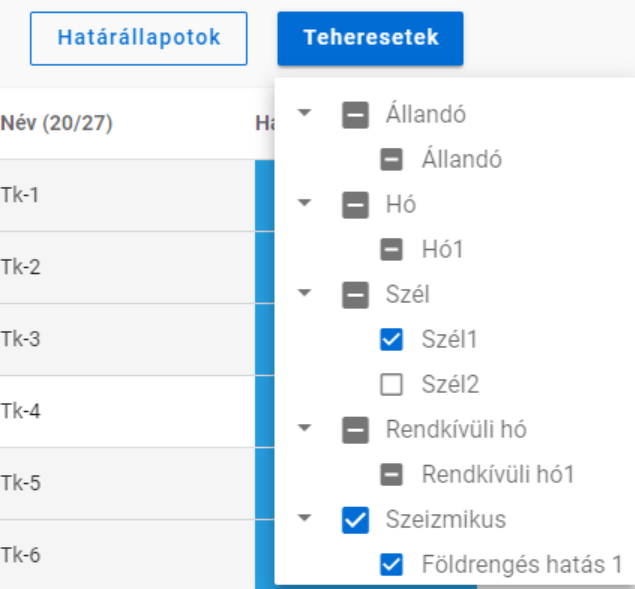
A jelölőnégyzeteknek három állása van. Nem csak kiválasztásra használhatóak, hanem egyben az adott teherkombináció csomag tartalmát is mutatják. Kézzel csak bepipált vagy üres állapotra kapcsolhatók, a köztes állás akkor jelenik meg, ha egyéb szűrőket alkalmazunk.
A határállapotok és teheresetek szerinti szűrést számítási eredmények nélkül is lehet alkalmazni.
A szabályok szerinti szűrés viszont minden esetben analízis vagy tervezési eredményeken alapszik. A különböző típusú szabályokat egyszerre vagy egymás után is lehet alkalmazni, hogy kiválasszuk a kívánt teherkombinációkat.
Amikor egy szabályt alkalmazunk, a filter megvizsgál minden teherkombinációt, ami ki volt választva a Teherkombináció csomag megadása ablakban -akár kézzel, akár határállapota vagy a benne lévő tehereset alapján-, minden olyan végeselem pontban, amit a szabály megkíván. Azok a teherkombinációk, amik megfelelnek a szabálynak, kiválasztva maradnak, míg azok, amelyek nem, nem lesznek többé kijelölve.
- Analízis szabály alkalmazásával deformációk vagy igénybevételek alapján választhatunk ki kombinációkat. Az analízis eredményeket a szabály megadásától függően minden végeselem pontban vagy csak az elemvégeken vizsgáljuk (pl. kapcsolatokhoz). Deformációkat csak SLS, míg igénybevételeket csak ULS kombinációkban vizsgálunk.
- Kihajlás szabállyal azok a teherkombinációk választhatók ki, amelyekhez tartozó rugalmas kritikus teherszorzó (első kihajlási sajátérték) kisebb a megadott értéknél.
- Kihasználtsági szabállyal a teherkombinációkat a kiválasztott részletmodell minden végeselem pontjában meghatározott kihasználtságok alapján lehet szűrni. Acél elemek esetén a kihasználtságok elérhetők minden szabványos vizsgálatból, mint pl. általános rugalmas szilárdsági ellenállás, tiszta igénybevételi ellenállás, interakciók és globális stabilitásvizsgálat. A filter csak ULS kombinációkra alkalmazható.
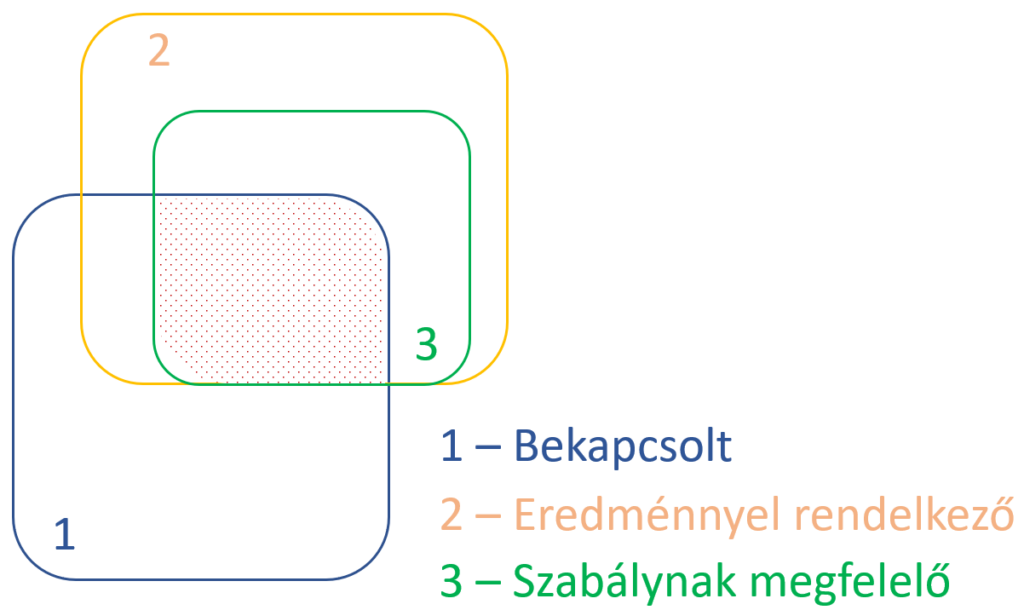
Különböző típusú szűrők kombinálása
A háromféle szűrőt lehetséges és érdemes együtt használni, azonban fontos tudni, hogy a szabályok szerinti szűrést csak azokon a kombinációkból válogat, amik ki vannak választva és van hozzájuk megfelelő számítási eredmény.
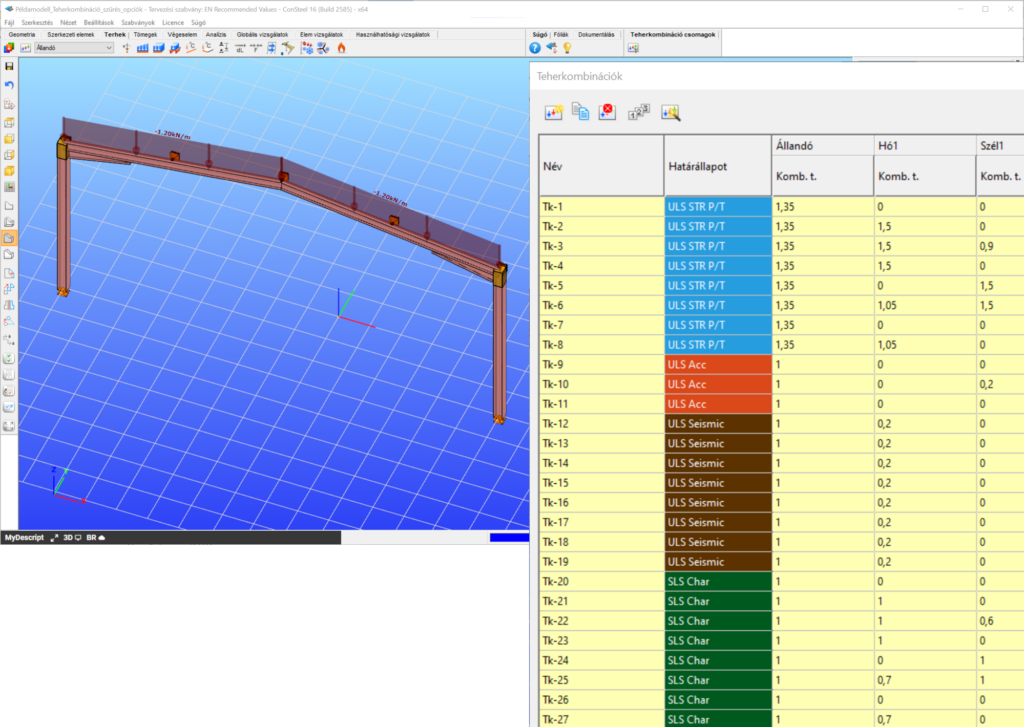
Vegyünk egy példát!
Egy egyszerű síkbeli keretmodell, amiben 27 teherkombinációt generáltunk többféle határállapotban. Az analízis és szabványos tervezési eredmények rendelkezésre állnak az összes teherkombinációban.
Alkalmazzunk egy kihasználtsági szabályt, amely kiválasztja azokat a teherkombinációkat, ahol a legnagyobb mértékadó kihasználtság 50% felett van.
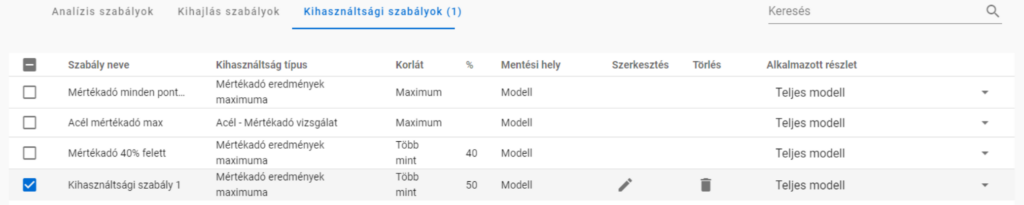
Ekkor négy teherkombinációt kapunk:
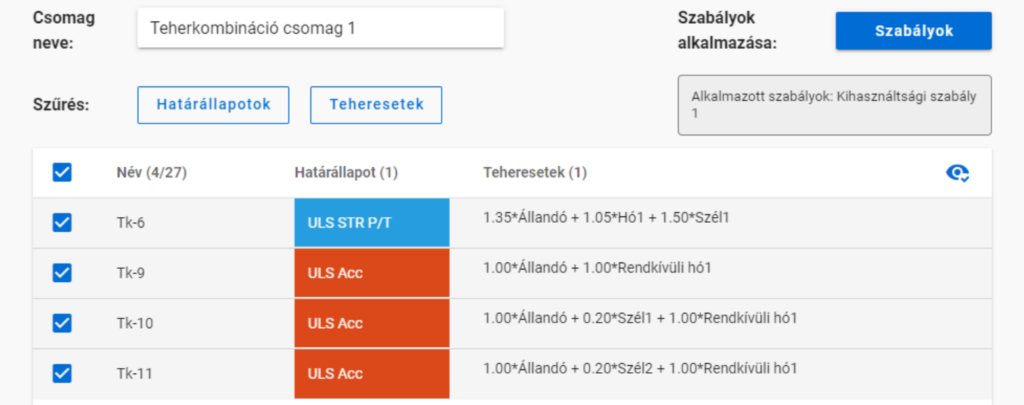
De ha az 50%-os szabály alkalmazása előtt kikapcsoljuk a rendkívüli teherkombinációkat,
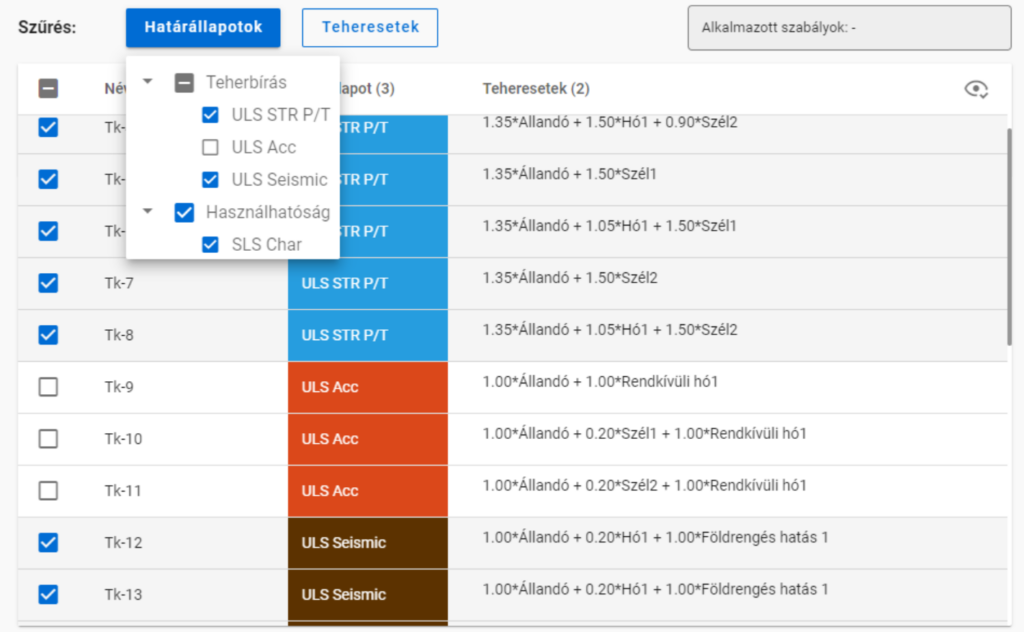
akkor a szabály alkamazása után már csak egy kombinációnk marad.
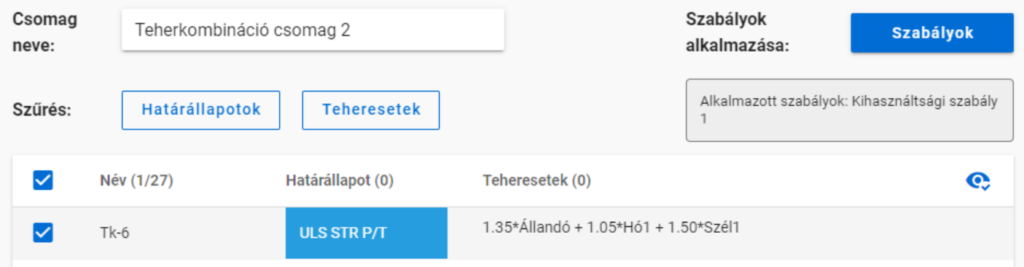
Több szabály alkalmazása
Több szabály együttes alkalmazása esetén a létrejövő teherkombináció-lista azoknak a listáknak az összege lesz, amik a szabály külön-külön való alkalmazása esetén jöttek volna létre.
gateIntroduction
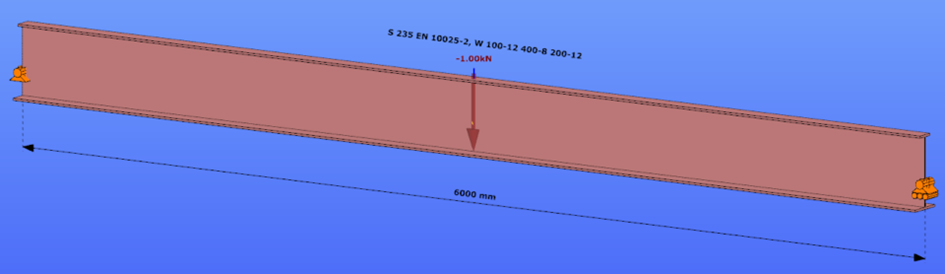
This verification example studies a simple fork supported beam member with welded section (flanges: 200-12 and 100-12; web: 400-8) subjected to bending about major axis. Constant bending moment due to concentrated end moments and triangular moment distribution from concentrated transverse force is examined for both orientations of the I-section. Critical moment and force of the member is calculated by hand and by the Consteel software using both 7 DOF beam finite element model and Superbeam function.
Geometry
Normal orientation – wide flange in compression
Constant bending moment distribution
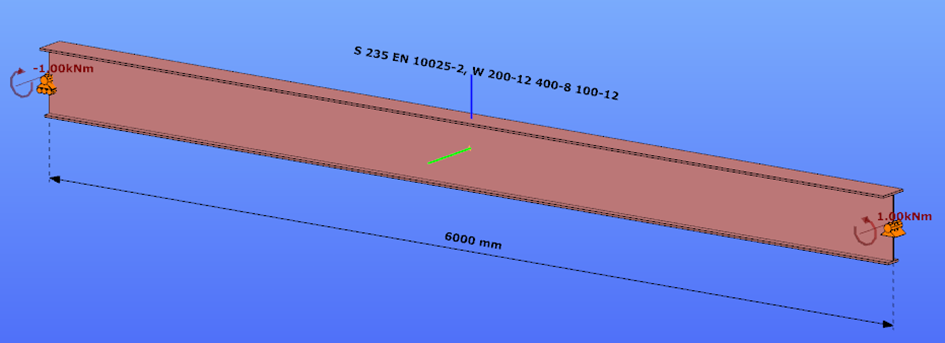
Triangular bending moment distribution – load on upper flange
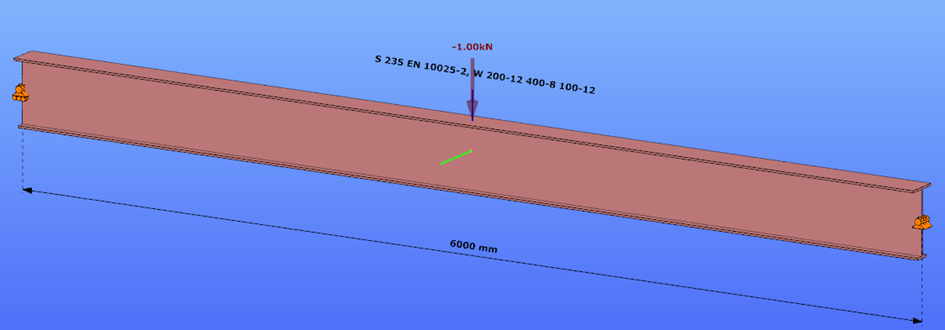
Triangular bending moment distribution – load on bottom flange
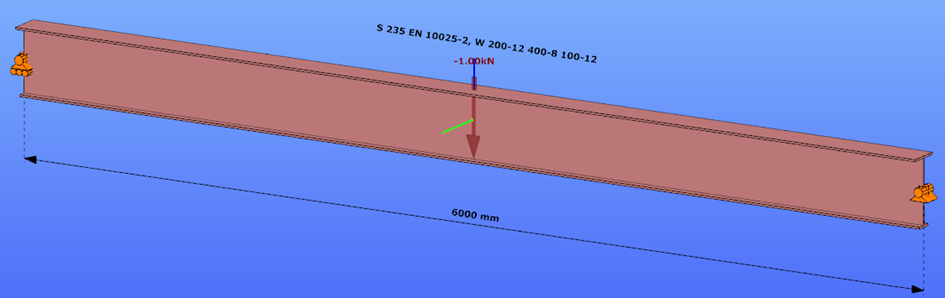
Reverse orientation – narrow flange in compression
Constant bending moment distribution
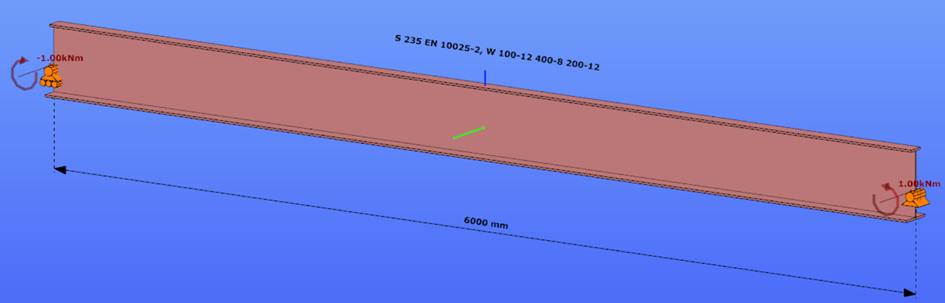
Triangular bending moment distribution – load on upper flange
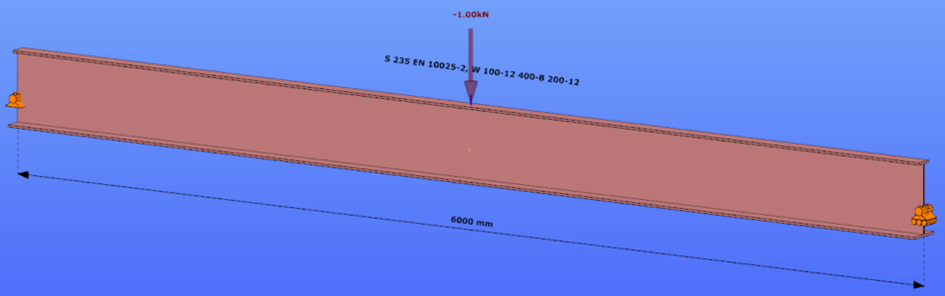
Triangular bending moment distribution – load on bottom flange
Calculation by hand
Factors to be used for analitical approximation formulae of elastic critical moment are taken from G. Sedlacek, J. Naumes: Excerpt from the Background Document to EN 1993-1-1 Flexural buckling and lateral buckling on a common basis: Stability assessments according to Eurocode 3 CEN / TC250 / SC3 / N1639E – rev2
Normal orientation – wide flange in compression
Constant bending moment distribution


Reverse orientation – narrow flange in compression


Computation by Consteel
Version nr: Consteel 15 build 1722
Normal orientation – wide flange in compression
Constant bending moment distribution
- 7 DOF beam element
First buckling eigenvalue of the member which was computed by the Consteel software using the 7 DOF beam finite element model (n=25). The eigenshape shows lateral torsional buckling.
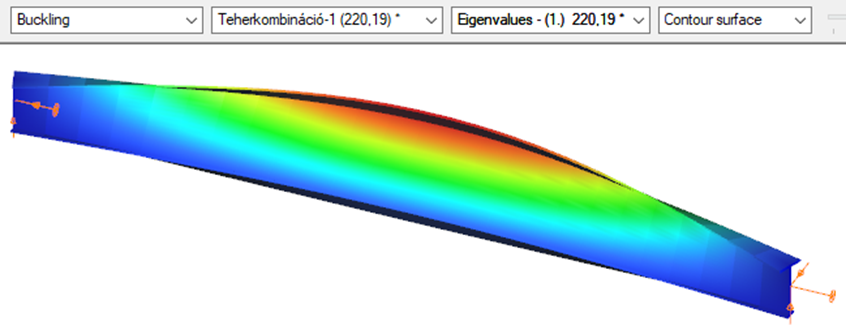
Superbeam
First buckling eigenvalue of the member which was computed by the Consteel software using the Superbeam function (δ=25).
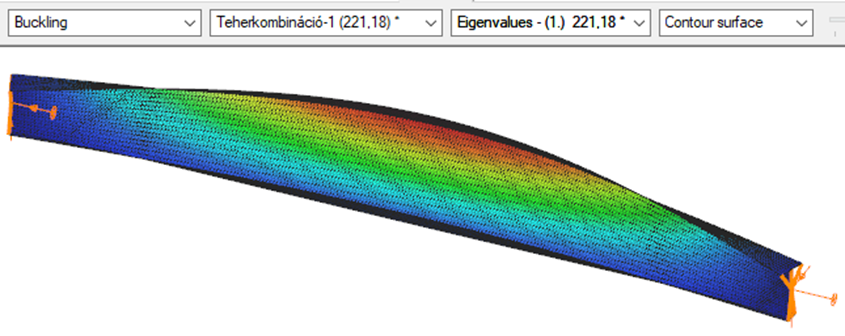
Introduction
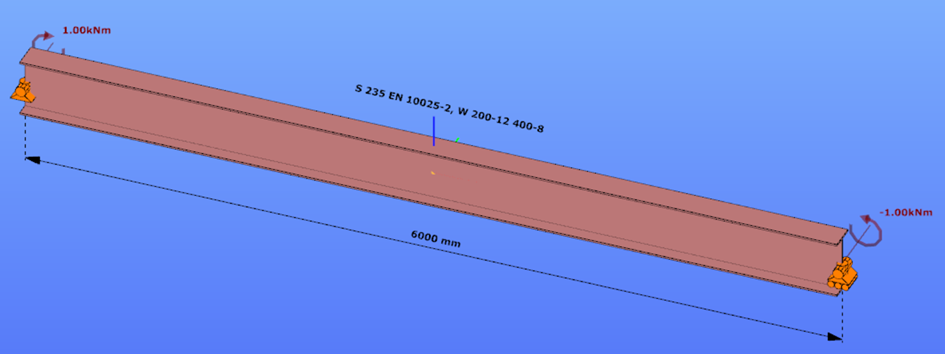
This verification example studies a simple fork supported beam member with welded section (flanges: 200-12; web: 400-8) subjected to bending about major axis. Constant bending moment due to concentrated end moments and triangular moment dsitribution from concentrated transverse force is examined. Critical moment and force of the member is calculated by hand and by the Consteel software using both 7 DOF beam finite element model and Superbeam function.
Geometry
Constant bending moment distribution
Triangular bending moment distribution – load on upper flange
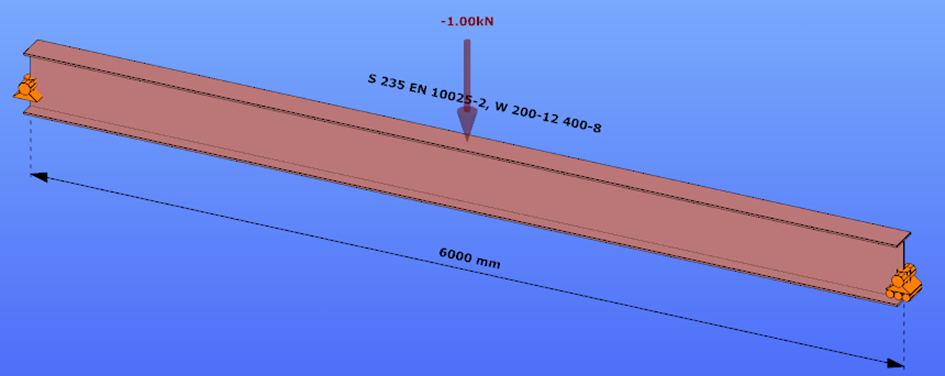
Triangular bending moment distribution – load on bottom flange
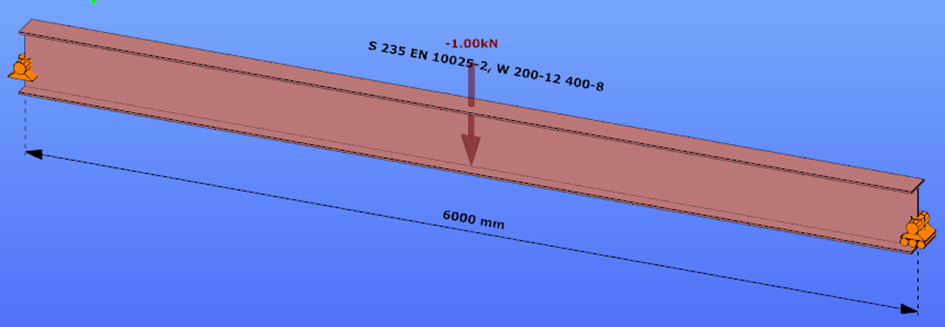
Calculation by hand
Constant bending moment distribution

Triangular bending moment distribution
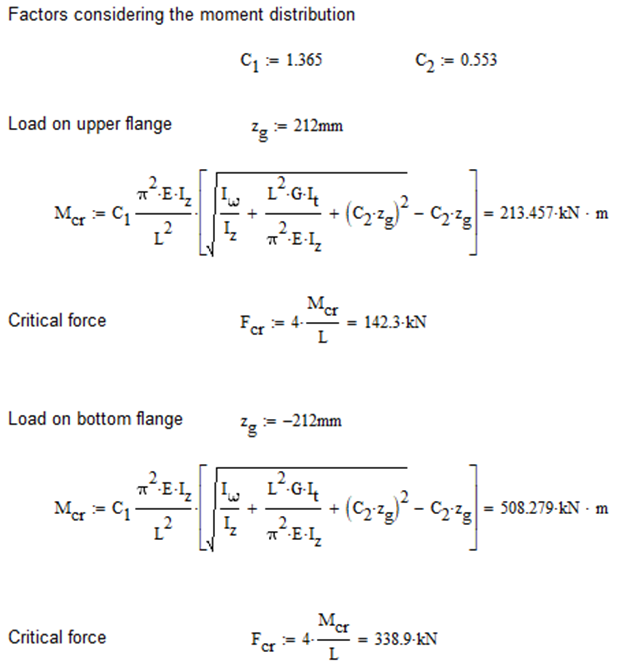
Computation by Consteel
Version nr: Consteel 15 build 1722
Constant bending moment distribution
7 DOF beam element
First buckling eigenvalue of the member which was computed by the Consteel software using the 7 DOF beam finite element model (n=16). The eigenshape shows lateral torsional buckling.
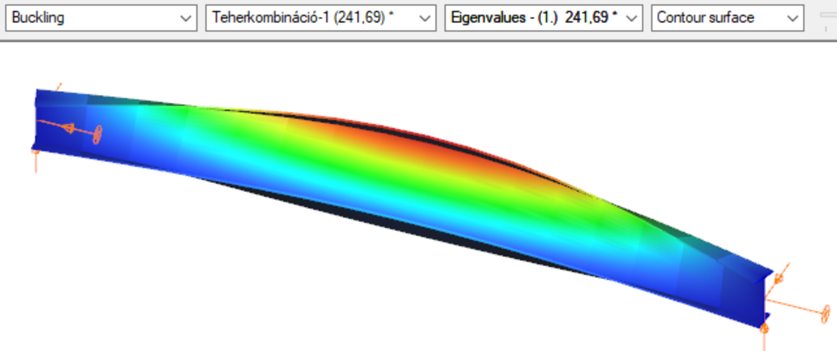
Superbeam
First buckling eigenvalue of the member which was computed by the Consteel software using the Superbeam function (δ=25).
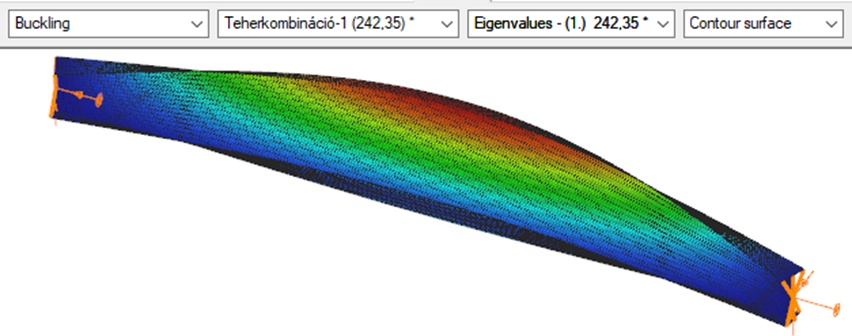
Triangular bending moment distribution – load on upper flange
7 DOF beam element
First buckling eigenvalue of the member which was computed by the Consteel software using the 7 DOF beam finite element model (n=16).
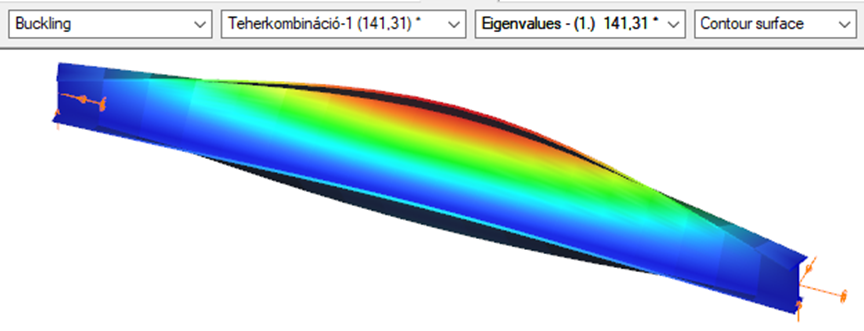
Superbeam
First buckling eigenvalue of the member which was computed by the Consteel software using the Superbeam function (δ=25).
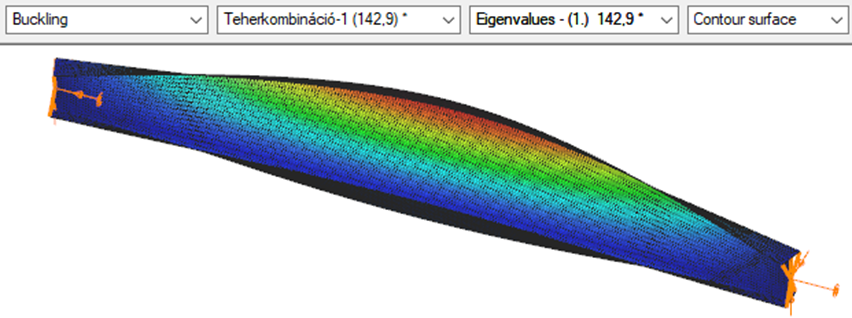
Triangular bending moment distribution – load on bottom flange
(tovább…)Introduction
This verification example studies a simple fork supported beam member with welded section equivalent to IPE360 (flanges: 170-12,7; web: 347-8) subjected to biaxial bending due to concentrated end moments and compression due to axial force. Second order deformations of the middle cross-section of the member are calculated by hand and by the ConSteel software using both 7DOF beam and shell finite elements and Superbeam function. In addition to the verification, the difference between modelling with 6DOF and 7DOF elements is demonstrated.
Geometry
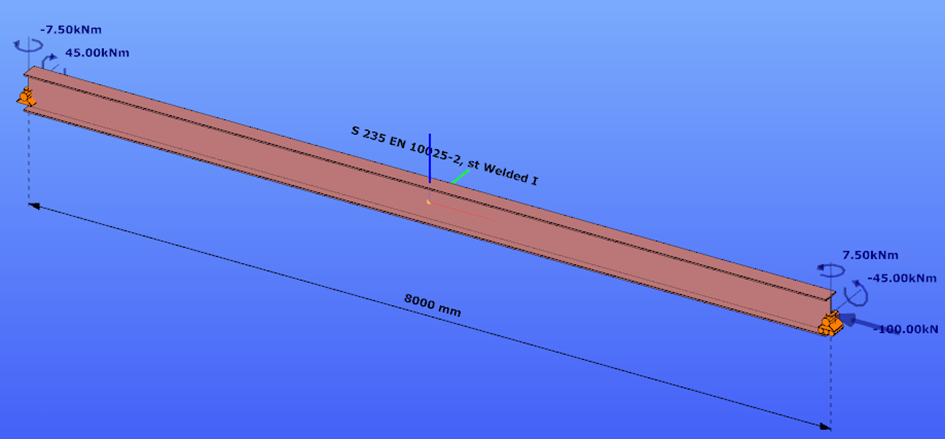
Calculation by hand
The first order and the simple amplified (P-δ) deformations can be analitically calculated by the well known formulas. The calculation of the second order deformations considering true, three-dimensional behaviour of the beam is however so complicated that there are only approximate analitical formulas available for hand calculation. The formula below can be found in Chen, W. and Atsuta, T.: Theory of Beam-Columns, Vol. 2: Space behavior and design, McGRAW-HILL 1977, p. 192


Computation by Consteel
Version nr: Consteel 15 build 1722
First order
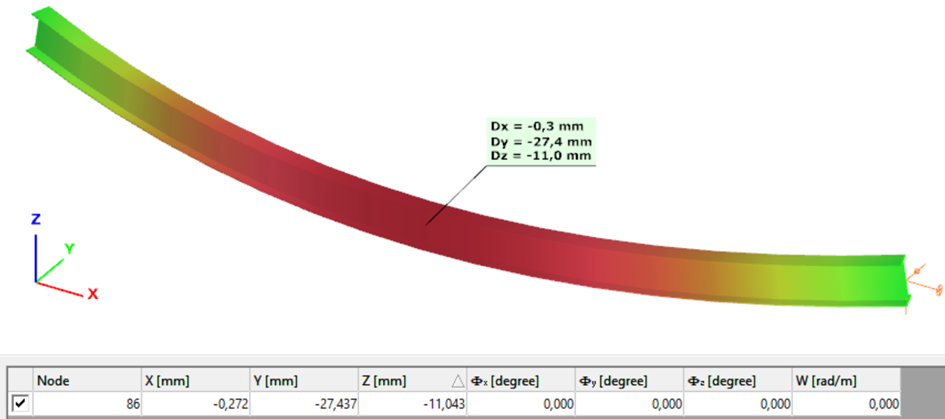
Second order – 6DOF beam element
The second order deformation of the member which was computed by the ConSteel software. It is visible that there is no torsion, only increments of the lateral displacements due to P-δ effect:
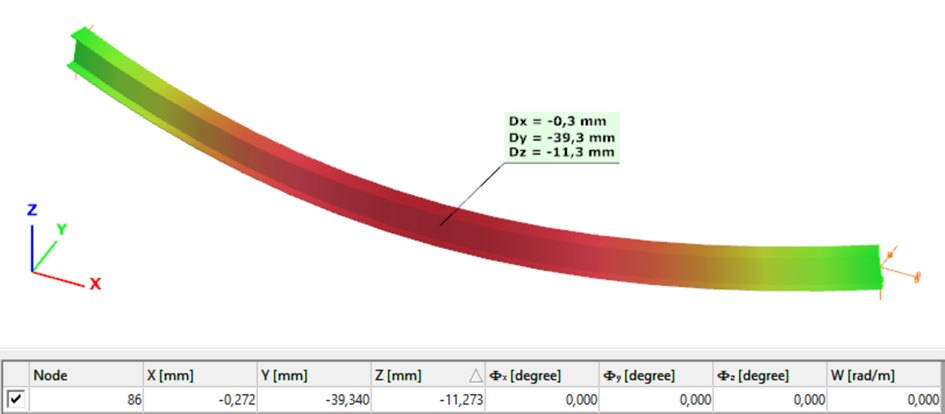
Second order – 7DOF beam element
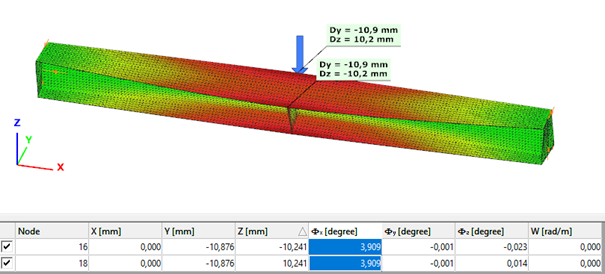
The second order deformation of the member which was computed by the ConSteel software using the 7DOF beam finite element model (n=16). It is visible that there is torsion and further increment in the lateral displacement (Dy):
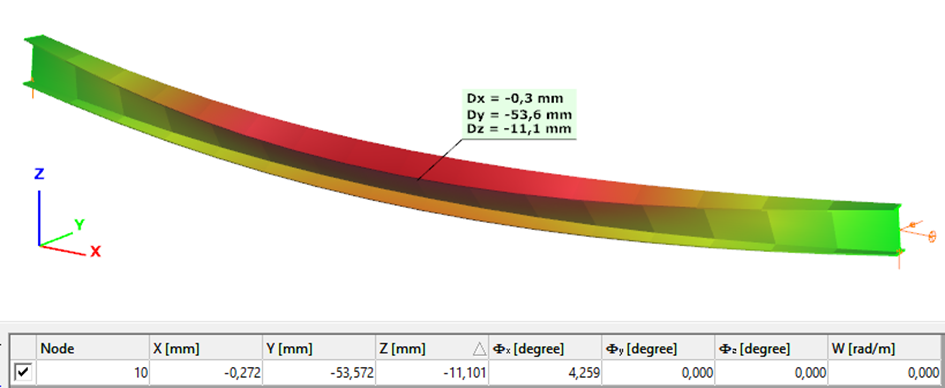
Second order – Shell finite element
The second order deformation of the member which was computed by the ConSteel software using the shell finite element model (δ=25mm):
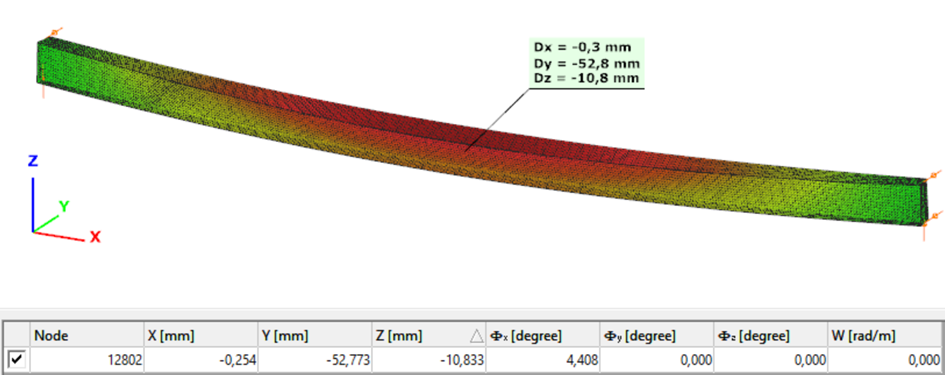
Second order – Superbeam
The second order deformation of the member which was computed by the ConSteel software using the Superbeam model (δ=25mm):
Introduction
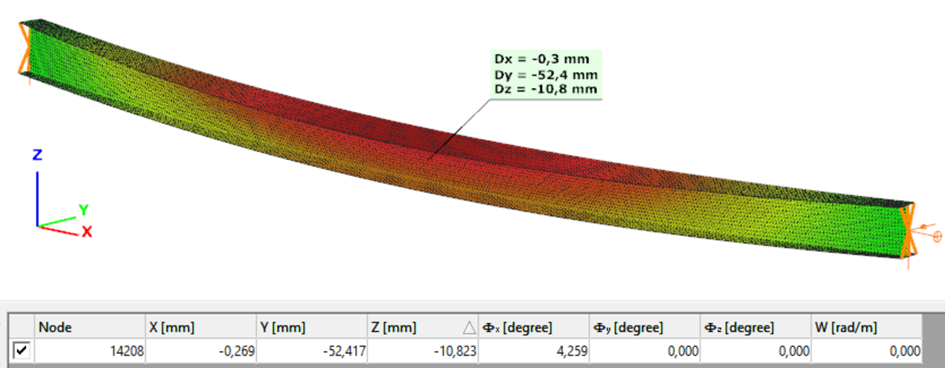
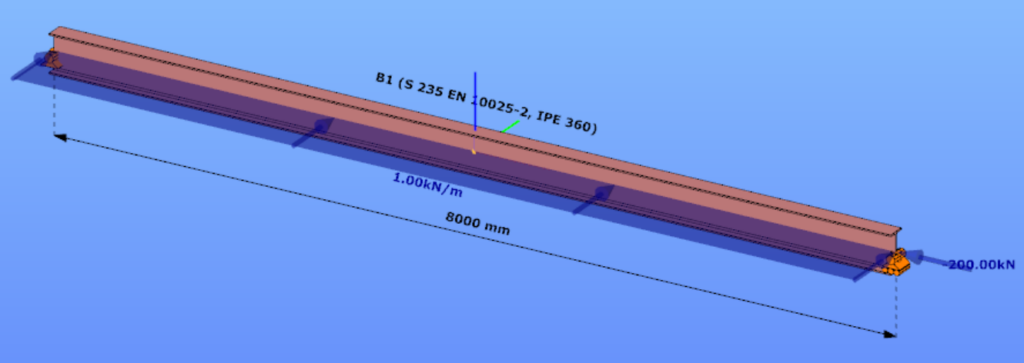
This verification example studies a simple fork supported beam member with IPE 360 section subjected to axial force and bending about the minor axis due to lateral, distributed force. The second order bending moment and the maximum axial compressive stress of the member is calculated by hand and by the Consteel software using the 7DOF beam finite elements.
Geometry
Calculation by hand

Computation by Consteel
Version nr: Consteel 15 build 1488
7DOF beam element The second order bending moment diagram of the member which was computed by the Consteel software using the 7DOF beam finite element model:
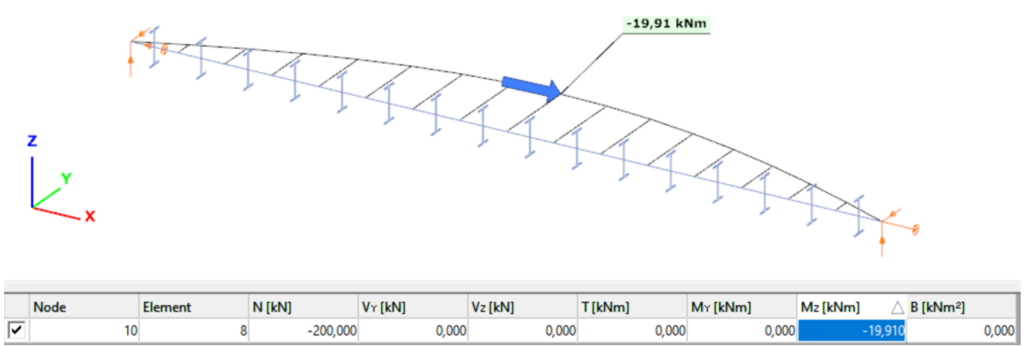
Normal stress in the middle cross-section:
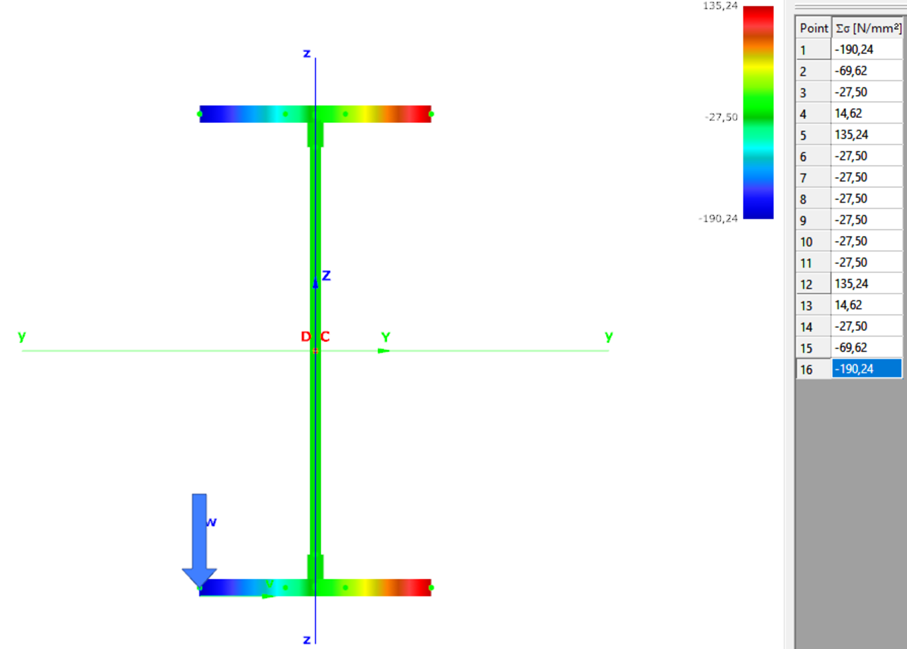
Introduction
Our verification examples are created to be able to compare hand calculation results with Consteel anaysis results with using either 7DOF beam or shell finite elements. This example is a member of mono-symmetric I- section loaded with transverse concentrated load.
Geometry
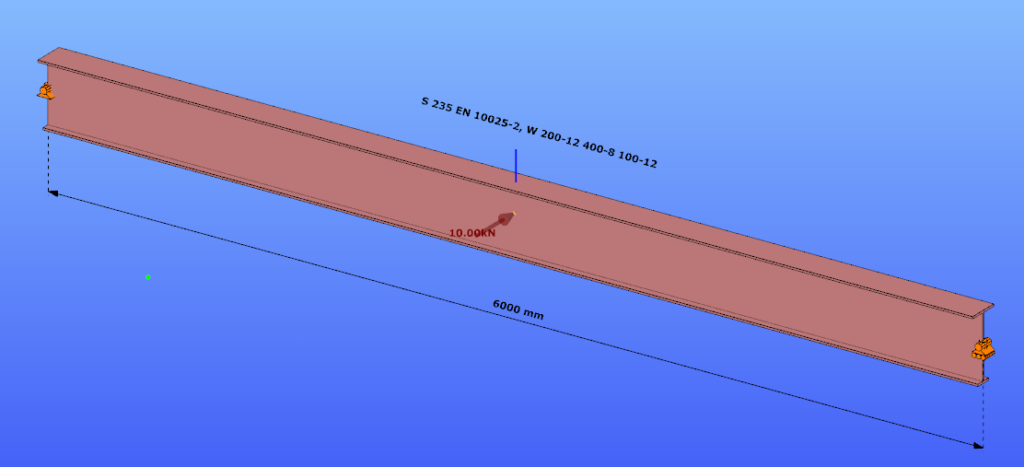
Calculation by hand

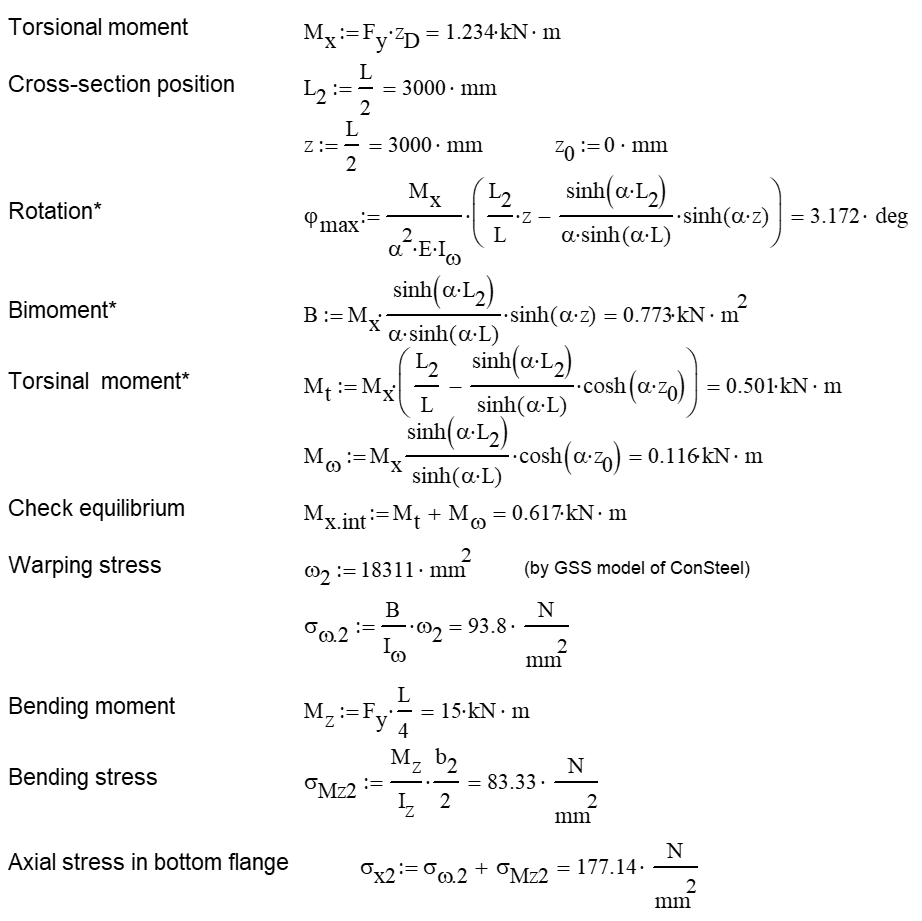
Computation by Consteel
Version nr: Consteel 15 build 1488
- 7DOF beam element
Deformation of the member with the numerical value of the maximum rotation (self-weight is neglected):
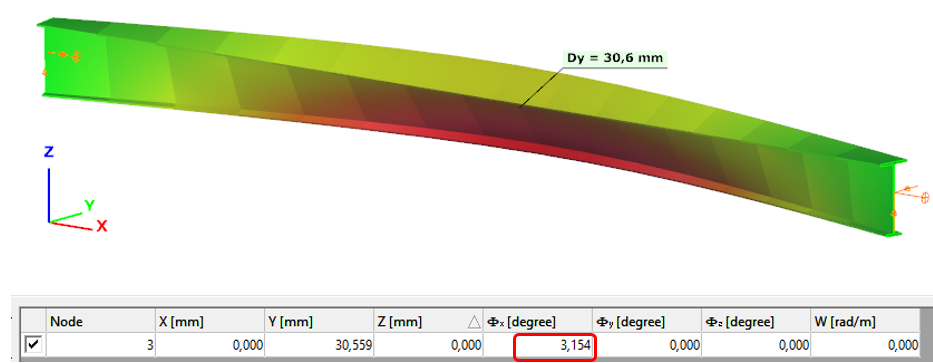
Introduction
Our verification examples are created to be able to compare hand calculation results with Consteel anaysis results with using either 7DOF beam or shell finite elements including Superbeam function. This example is a member in torsion loaded with concentrated torque.
Geometry
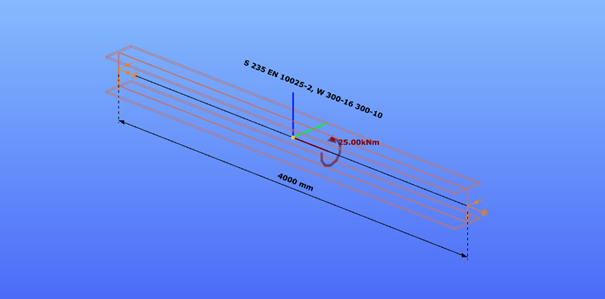
Calculation by hand


Computation by Consteel
Version nr: Consteel 15 build 1488
- 7DOF beam element
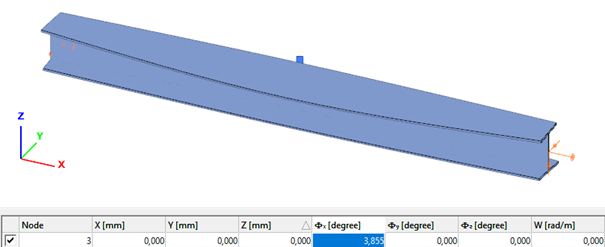
Deformation of the member due to concentrated twist moment:
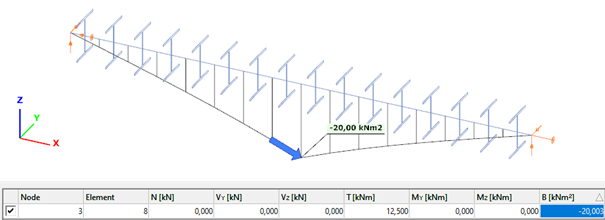
Bimoment of the member due to concentrated twist moment:
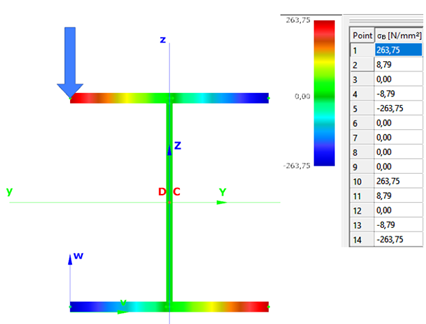
Warping normal stress in the middle cross-section:
- Shell FE model
Maximum deformation of the middle cross-section: