In this article, we aim to answer the question: Why are there two different procedures for exporting connections to IDEA StatiCa? Let’s explore the difference between using the Connection interface and Checkbot export.
IDEA StatiCa Connection
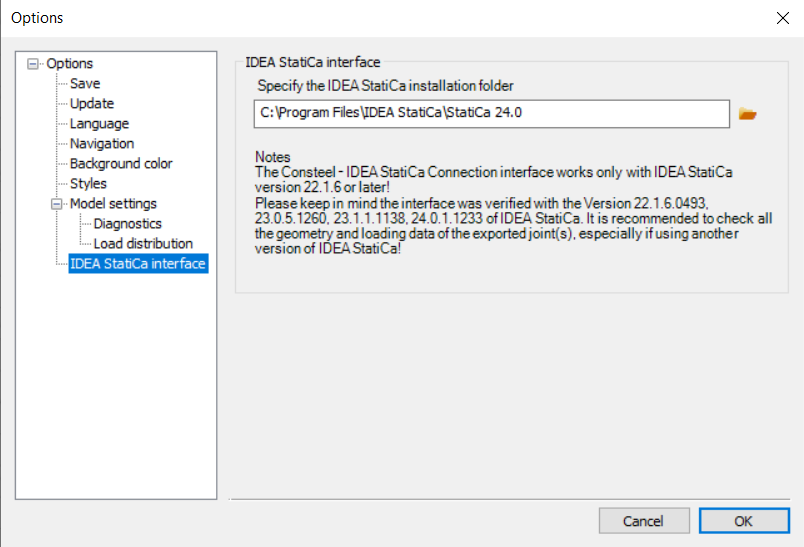
In order to use the IDEA StatiCa Connection link, please make sure that the program is installed and that the folder location is specified in the IDEA StatiCa Interface ‘Options menu‘.
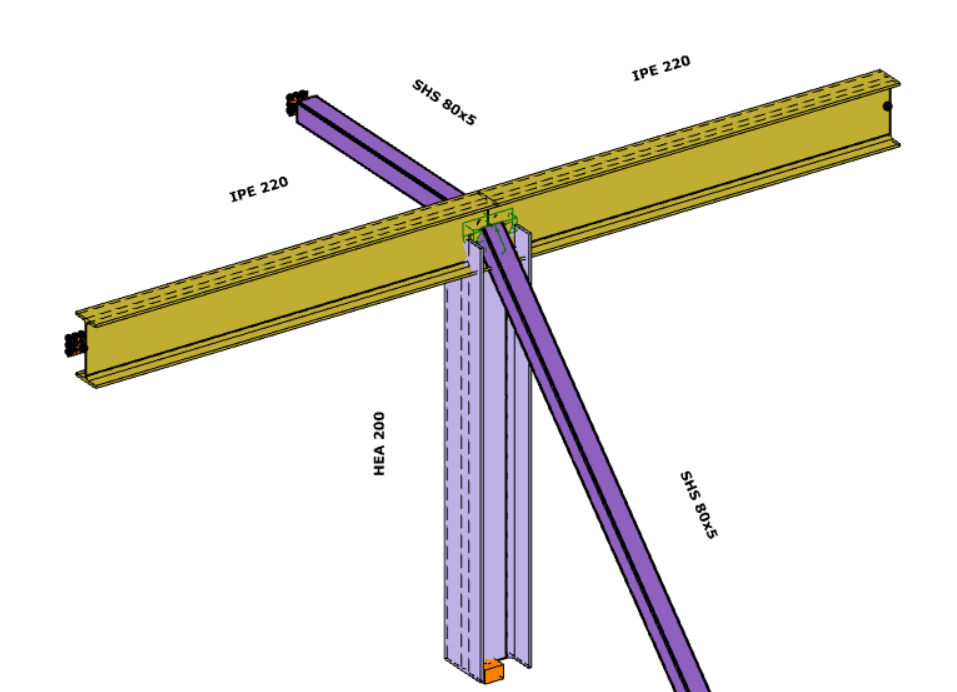
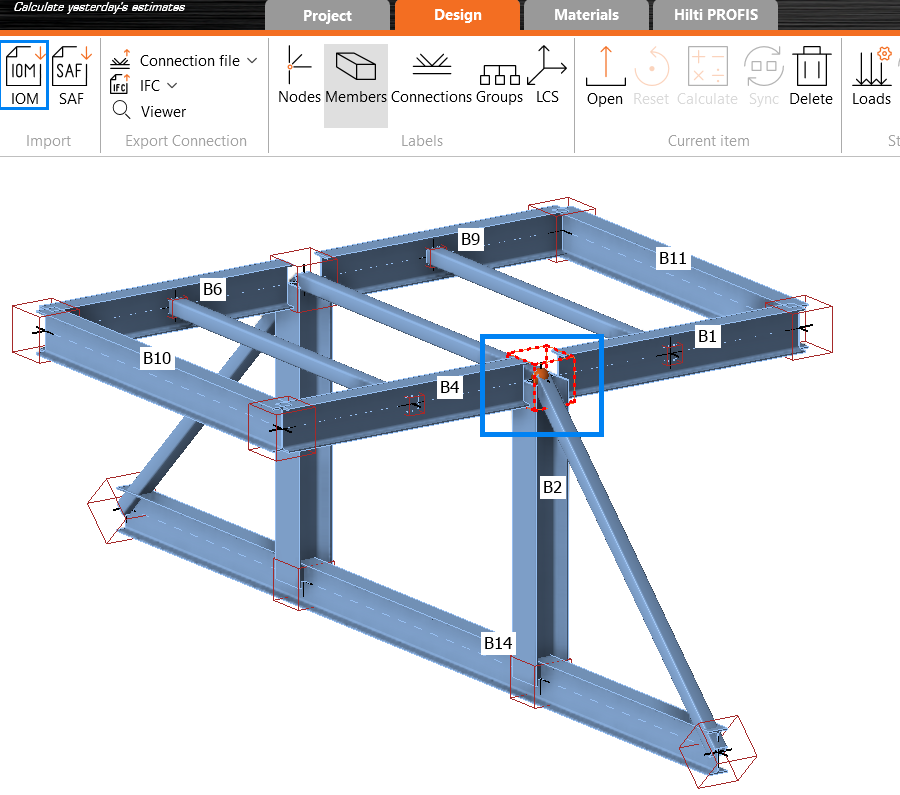
The conversion starts on the Structural Members tab, using the ‘Create Joint by Model‘ function. After selecting the appropriate intersection between members, a new window will appear.
If the ‘IDEA StatiCa Connection’ type is selected, the IDEA StatiCa application will launch automatically, and the selected connection will be transferred.
Using this method and placing the joints into the Consteel model (possible in multiple positions with similar geometry), a direct connection is established between the two programs. This means that geometry (cross sections, materials) and internal forces (according to all combinations of locations where the joint is placed) are taken directly from Consteel.
IDEA StatiCa Checkbot
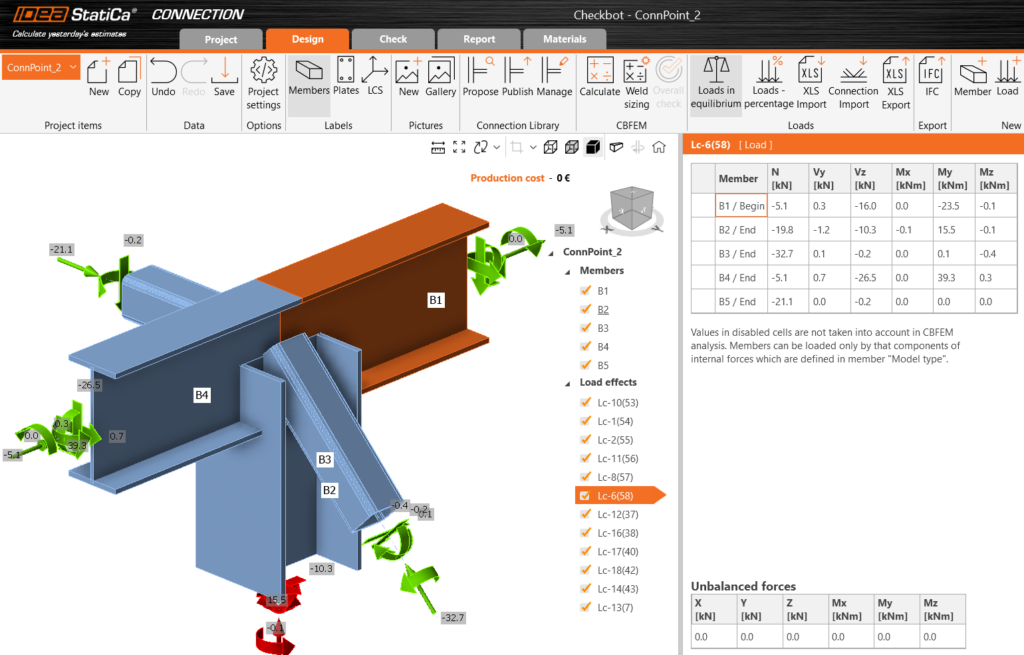
The IDEA StatiCa Checkbot export can be accessed from the ‘File menu’ by selecting it from the ‘Exports section’. Users must define a location where the entire model will be exported in .xml format. This file can later be imported into IDEA StatiCa Checkbot using the IOM (IDEA Open Model) import option.
The full 3D model is imported using this method, and all joints can be analyzed individually within the IDEA StatiCa. A list of all imported items will appear in IDEA, each marked with a status such as ‘Checked’ or ‘Not Checked’. The imported members can be visualized in 3D, along with the applied loads.
The conversion supports materials, cross-sections, and load combination management. The internal forces resulting from the Consteel analysis for ULS combinations are available in IDEA StatiCa. This approach also ensures that the internal coordinate systems for all internal forces are preserved accurately.
All connections present in the imported model can be exported to IDEA StatiCa Connection, where joint design is carried out. You can choose to export a single connection or select multiple connections and save them in one file, allowing you to design the connection or print reports for all modeled connections at once.
Connections designed in Checkbot can only be considered in the global analysis phase in Consteel if the calculated stiffness is manually introduced at the release ends.
When to choose the direct link to IDEA StatiCa Connection?
Use direct link IDEA StatiCa Connection when you want to jump directly to the connection design in IDEA. Since the joint can be placed in multiple locations within the Consteel model, all internal forces from all combinations and all positions where the joint is placed will be taken into account.
A key advantage is that if you’re still working on your 3D model and changes occur, there’s no need to regenerate the link, simply update and verify the changes directly in IDEA StatiCa.
When to use IDEA StatiCa Checkbot Export?
Use Checkbot export when your structure contains many irregular or complex joints.For instance, if the bars in the connections do not intersect at a single point due to eccentricities or lack of space, you can merge them into one connection using Checkbot.
Conclusion
In summary, from the perspective of model updates and quicker access, using the direct connection via IDEA StatiCa Connection is generally the better choice, especially if the integrated Consteel Joint doesn’t provide enough flexibility for joint creation.
IDEA StatiCa Checkbot export offers significant advantages in terms of automated member recognition, possibility to merge joints, accurate assignment of internal forces, and efficient bulk joint analysis. It eliminates the need to manually verify force directions or coordinate systems, streamlining the workflow, especially for larger or more complex structures.
The main limitation of Checkbot export is that it establishes a one-way connection: every time the Consteel model changes, a new export is required in order to stay updated with the changes. Therefore, the choice between methods should depend on the nature of your project, if the model is expected to change frequently, the direct connection is more suitable. However, if you’re working with the final geometry and need to verify complex joints, the Checkbot export is the better option.
Did you know that Consteel provides a plugin to integrate structural modeling and analysis into your parametric Grasshopper definitions?
Download Pangolin from food4rhino.com or the Yak package manager of Rhino. You can also download it by logging in to our website. See Downloads/Plugins menu:
How will you possibly work in Pangolin? See the related videos on our YouTube channel, starting with the ‘Introducing Pangolin‘ video.
If you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free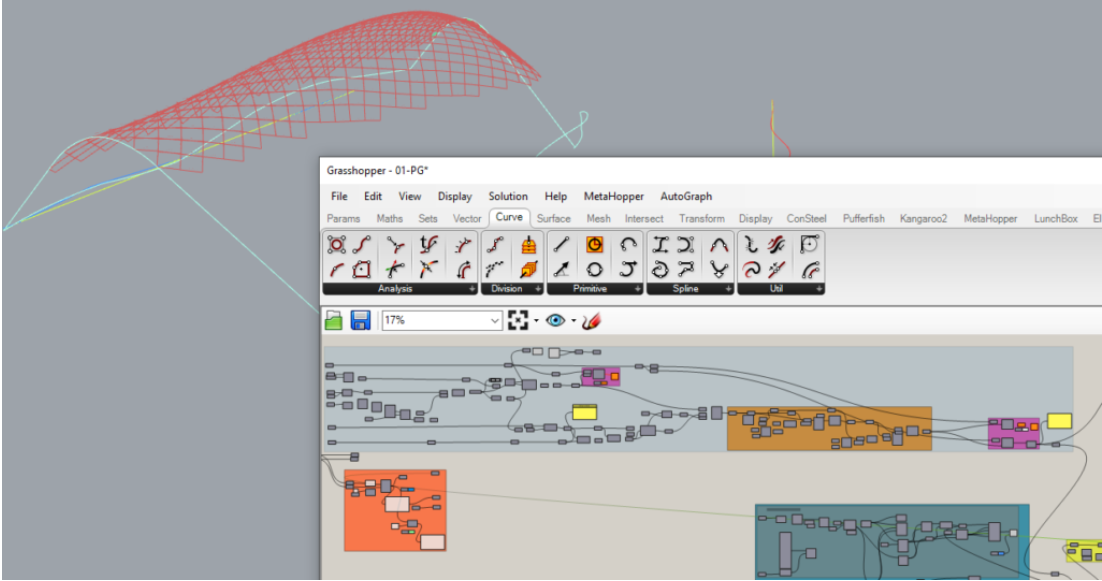
In Consteel, the calculation of cross sectional interaction resistance for Class 3 and 4 sections is executed with the modified Formula 6.2 of EN 1993-1-1 with the consideration of warping and altering signs of component resistances. Let’s see how…
Application of EN 1993-1-1 formula 6.2
For calculation of the resistance of a cross section subjected to combination of internal forces and bending moments, EN 1993-1-1 allows the usage -as a conservative approximation- a linear summation of the utilization ratios for each stress resultant, specified in formula 6.2.
$$\frac{N_{Ed}}{N_{Rd}}+\frac{M_{y,Ed}}{M_{y,Rd}}+\frac{M_{z,Ed}}{M_{z,Rd}}\leq 1$$
As Consteel uses the 7DOF finite element and so it is capable of calulcating bimoment, an extended form of the formula is used for interaction resistance calculation to consider the additional effect.
$$\frac{N_{Ed}}{N_{Rd}}+\frac{M_{y,Ed}}{M_{y,Rd}}+\frac{M_{z,Ed}}{M_{z,Rd}}+\frac{B_{Ed}}{B_{Rd}}\leq 1$$
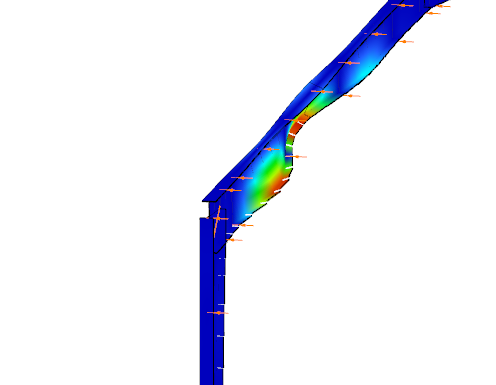
Formula 6.2 ignores the fact that not every component results the highest stress at the same critical point of the cross-section.
In order to moderate this conservatism of the formula, Consteel applies a modified method for class 3 and 4 sections. Instead of calculating the maximal ratio for every force component using the minimal section moduli (W), Consteel finds the most critical point of the cross-section first (based on the sum of different normal stress components) and calculates the component ratios using the W values determined for this critical point. Summation is done with considering the sign of the stresses caused by the components corresponding to the sign of the dominant stress in the critical point.
(For class 1 and 2 sections, the complex plastic stress distribution cannot be determined by the software. The Formula 6.2 is used with the extension of bimoments to calculate interaction resistance, but no modification with altering signs is applied)
Example
Let’s see an example for better explanation.
GATEDid you know that you could use Consteel to calculate rotational stiffness for bolted column/beam moment bearing connections?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for freeBolted connection
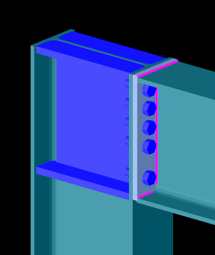

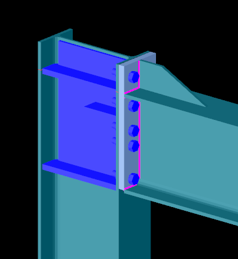
Bolted connection


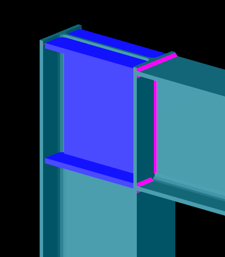
Welded connection

Did you know that you could use Consteel to perform dual analysis with 7DOF beam and/or shell elements?
With two advanced features, Superbeam and Convert members to plates, you can choose the approach that best suits your project needs, whether you’re focused on modeling efficiency or detailed analysis.
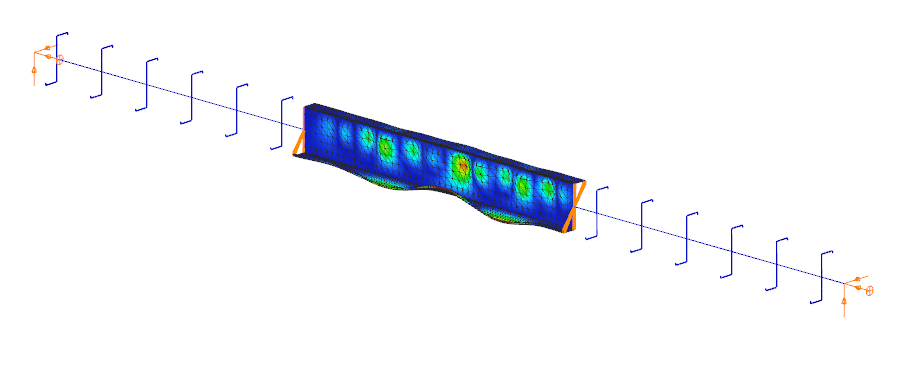
The Superbeam function offers a smart, adaptive way to handle structural members. It enables you to model with the simplicity of standard 7DOF beam elements while allowing you to switch to a more detailed shell-based analysis for specific members whenever needed.
Once the structure is modeled using beam elements, you can select how each member is analyzed:
- Using the beam model, which applies Consteel’s proven 7DOF beam elements along with its comprehensive design tools.
- Or using a shell model, which is automatically generated for selected members. This shell model includes detailing features such as web cutouts and stiffeners, fully integrated into the global analysis model.
This dual approach is fully adaptive. You can continue modifying your model using beam elements and switch between analysis modes as required, offering both speed and precision within the same workflow.
For a complete overview of how to activate and manage Superbeam functionality, refer to the documentation:
Superbeam – Consteel Manual

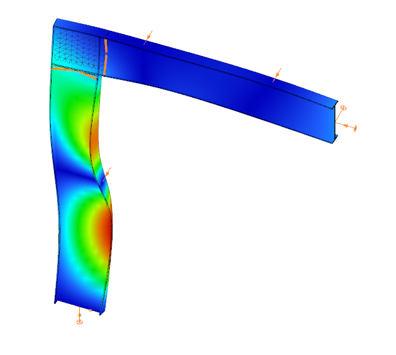

When you need complete control over geometry and mesh, or when shell analysis alone is not sufficient, Consteel provides the Convert members to plates function. This tool allows you to manually transform selected members into actual plate elements, enabling detailed modeling from the start.
Unlike the automatic conversion used in Superbeam, this method performs a permanent, non-reversible transformation (though undo is available during the session). It supports a wide range of section types, including hot-rolled, cold-formed, and welded profiles.
The conversion process preserves and adapts existing connections, eccentricities, loads, and supports. Where needed, rigid bodies and constraint elements are added to maintain structural continuity. These constraints ensure proper transfer of deformations, including warping, between the new plate model and the rest of the structure.
This function is especially useful in cases where precision is critical, such as modeling joints, fabrication-specific details, or complex load interactions.
To learn more, see the full guide here:
Convert Members to Plates – Consteel Manual
Both Superbeam and Convert members to plates serve different purposes, depending on the level of detail and control required in your model:
| Feature | Superbeam | Convert members to plates |
| Workflow | Beam modeling with optional shell analysis | Full plate modeling from the beginning |
| Conversion | Automatic and reversible | Manual and permanent |
| Suitable For | Flexibility in analysis, quick modeling | Full control, high-detail requirements |
| Supported Sections | Welded I and H profiles | Hot-rolled, cold-formed, and welded sections |
| Detailing Support | Cutouts and stiffeners (in shell analysis) | Full geometric detailing, including transitions |
| Design Integration | Integrated with beam-based design tools | Suitable for fabrication-level modeling |
In Superbeam, constraint elements are generated automatically to connect converted shell elements to other members, such as bars. During member-to-shell conversion, these elements link the FE shell nodes to the rest of the model, ensuring accurate deformation transfer.
If the convert members to plate function is applied directly to beam elements, rigid bodies are created at their ends, which is useful for analyzing local behavior but does not transfer warping deformations. If the beam is first converted to a shell and then to plates, hinged rigid edges are placed along the plate boundaries. This arrangement, combined with constraint elements, transfers not only in-plane and out-of-plane deformations but also warping between the shell and the rest of the structure.
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for freeDid you know that you could use Consteel to design web-tapered members?
Tapered members are widely used in the economic design of steel-framed structures, such as industrial halls and warehouses, because they make it possible to save material while still ensuring structural strength and stability. With Consteel’s dedicated Tapered Member function, you can model, analyze, and verify these members efficiently, supporting both everyday engineering practice and advanced stability checks.
In Consteel, tapered members are line members with welded I or H, box, or cold-formed C sections. Hot-rolled and other macro sections cannot be tapered. Their section height can vary linearly along the member length, making them suitable for realistic structural modeling.
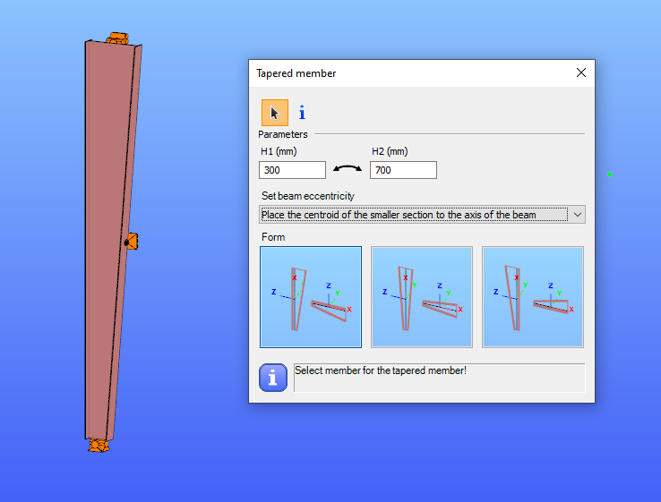
It is best to start with a section close to the smaller end of the taper. The start height (H1) applies at the beginning of the member, and the end height (H2) at the other end. If either value is less than half of the original section height, Consteel automatically resets it to 0.5 times the original. H1 and H2 can be swapped easily with the dedicated icon to reverse the taper direction.
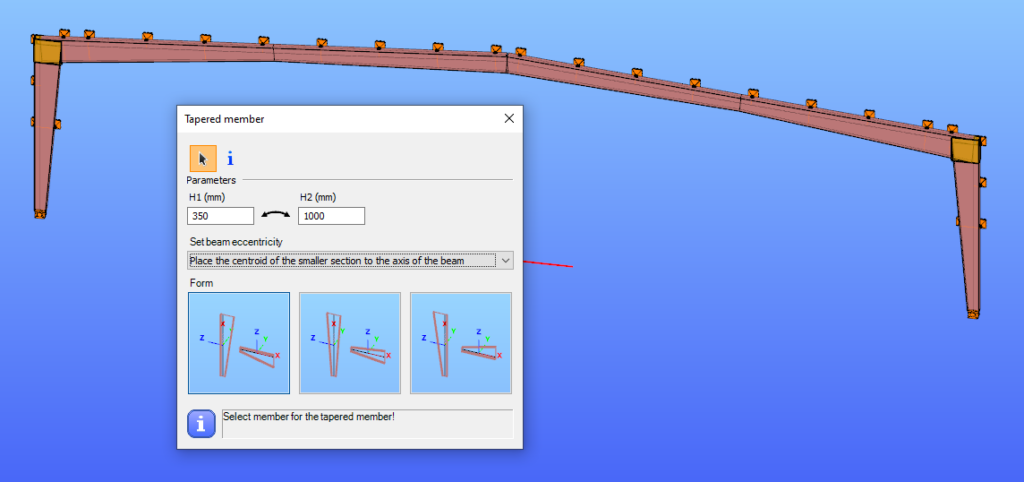
The placement of a tapered member relative to the axis of the original beam is defined by beam eccentricity rules. Consteel offers three alignment options:
- Centroid of the smaller section on the axis – the tapering develops outward from the end with the smaller height.
- Centroid of the larger section on the axis – the bigger end of the member remains fixed to the original axis.
- Centroid of the original section on the axis – one edge of the tapered member coincides with the original section, and the tapering starts from this position.
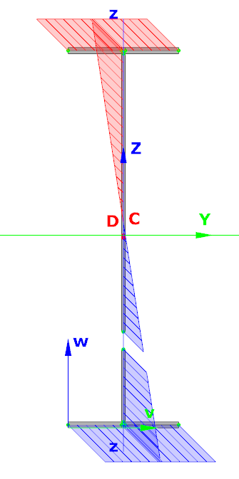
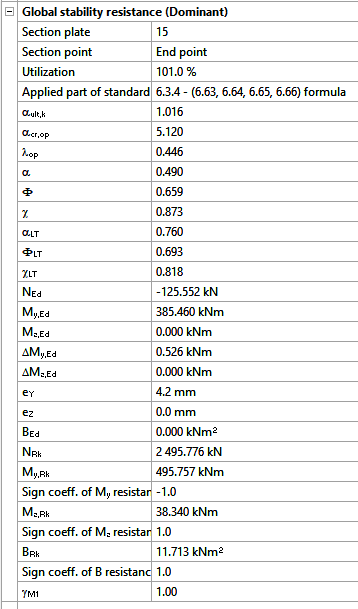
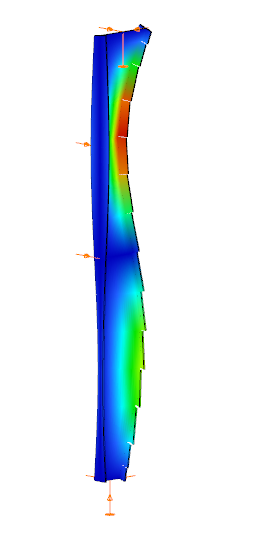
In analysis, Consteel creates tapered sections with the specified start and end heights and places them on the member’s reference line. Unless symmetric tapering is used, this placement is eccentric, which introduces additional effects. At frame joints, for example, extra moments from eccentric axial forces must be considered to maintain equilibrium.
Consteel handles these effects automatically, ensuring realistic results. Symmetric tapering keeps the analysis simpler, while eccentric tapering requires more attention. In all cases, global stability checks should complement sectional verifications to guarantee structural safety.
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
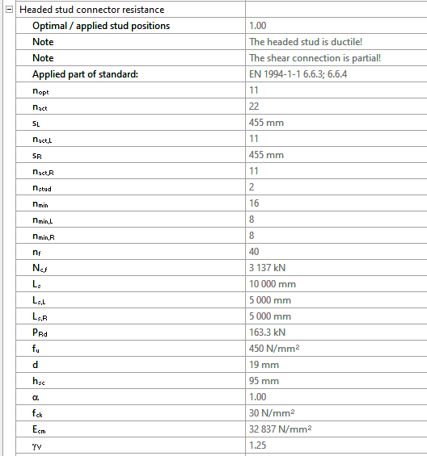
Try Consteel for freeDid you know that you could use Consteel to determine the optimum number of shear connectors for composite beams?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free
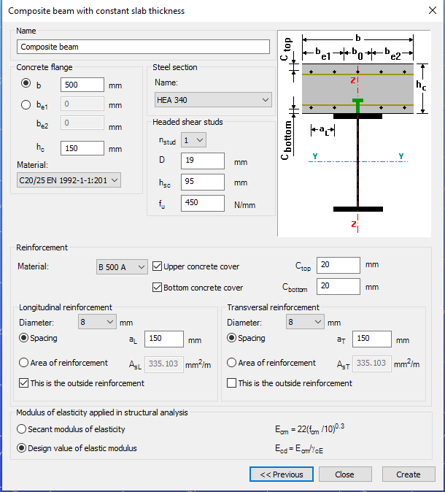

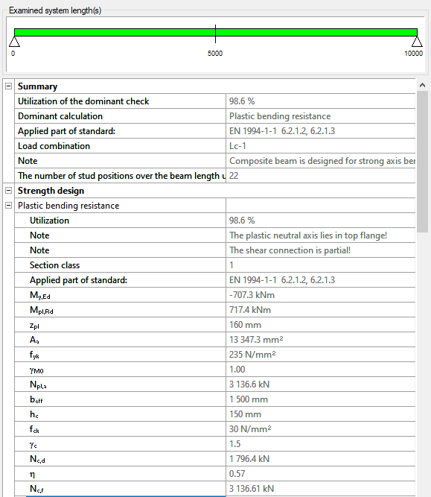
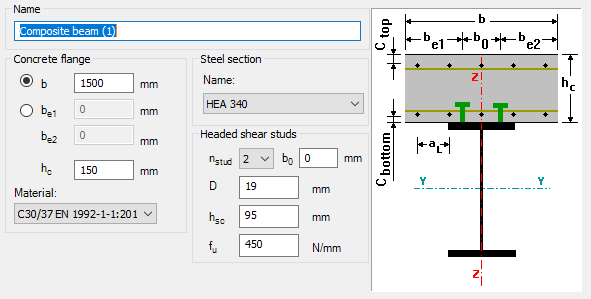
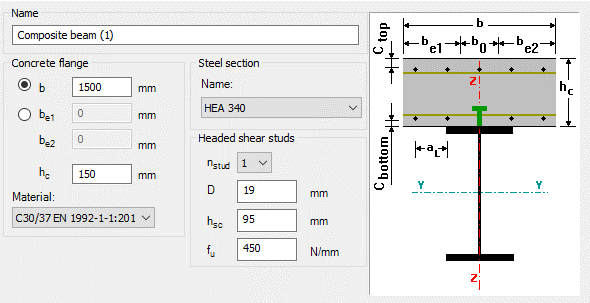
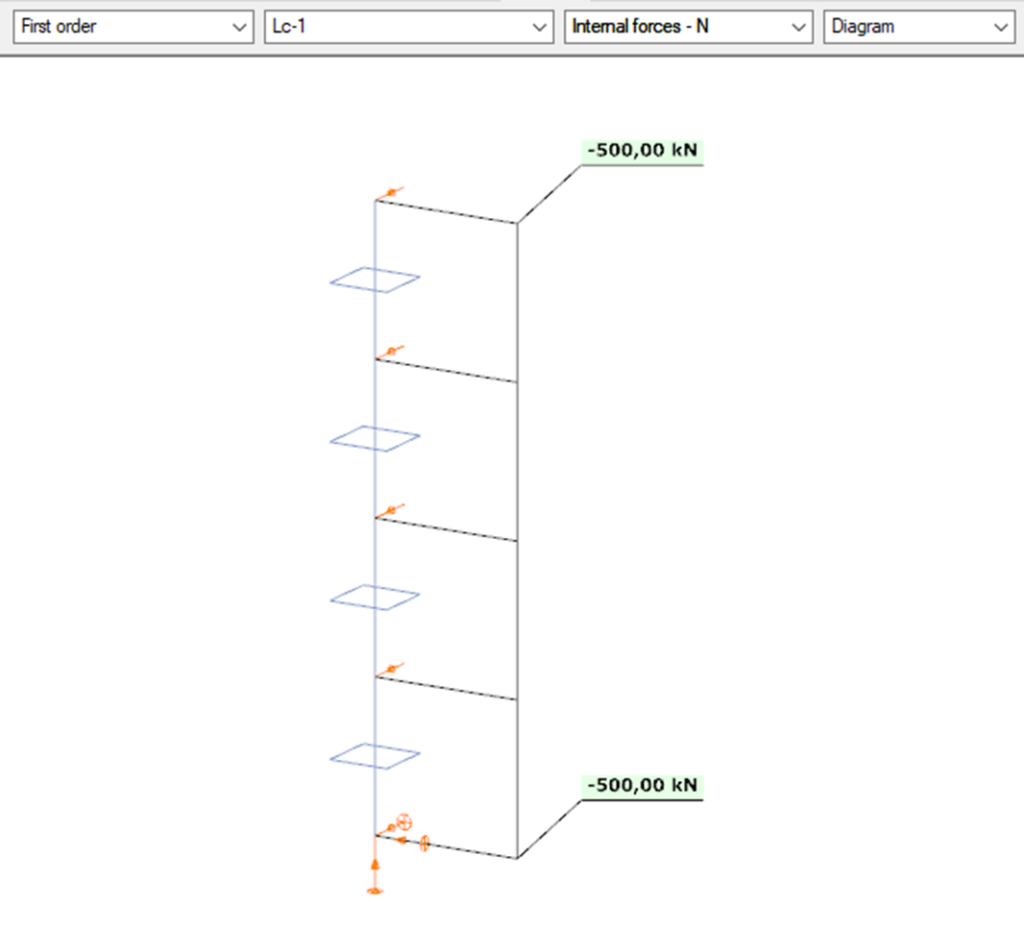
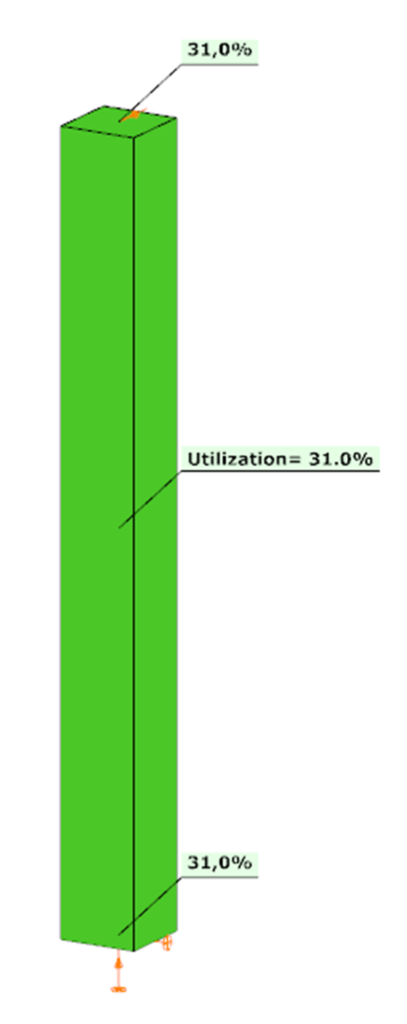
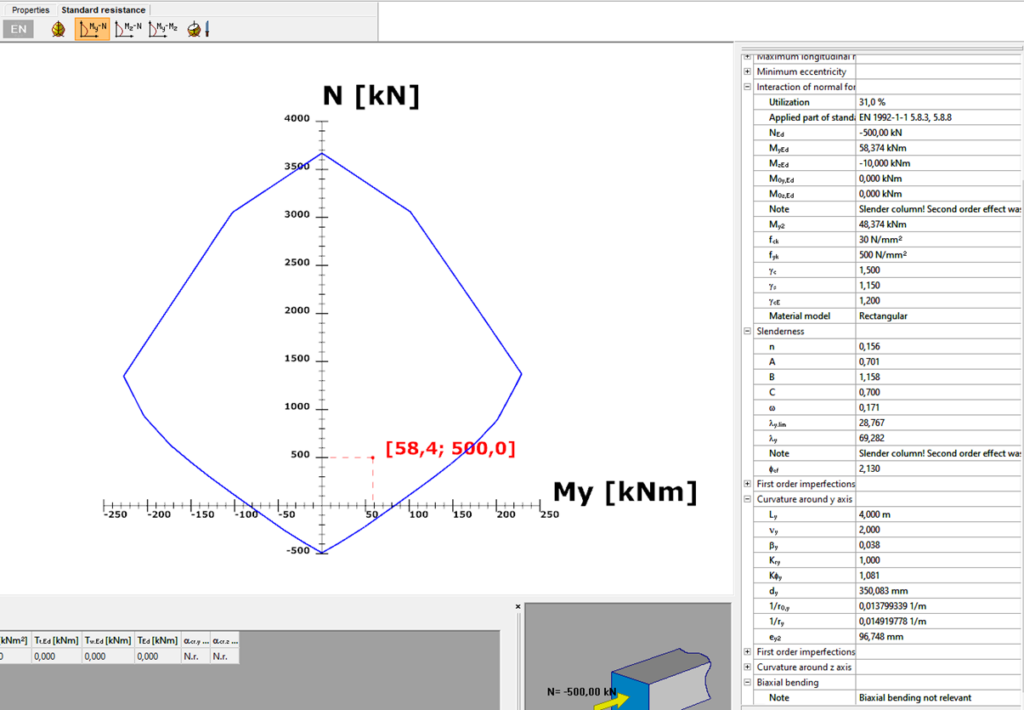
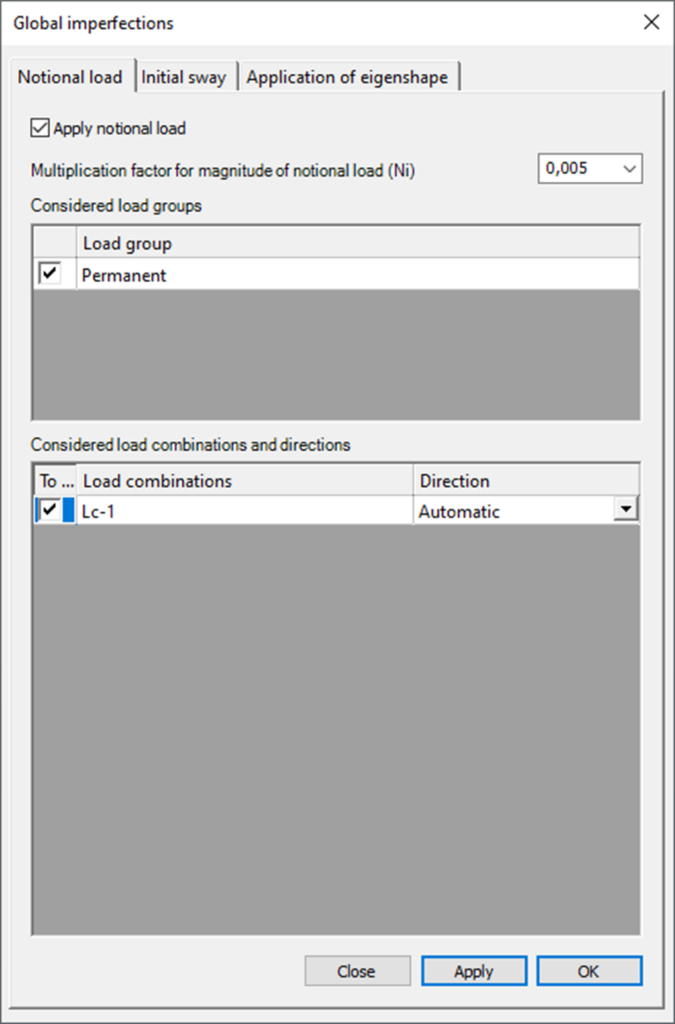
Did you know that you could use Consteel to determine automatically the second order moment effects for slender reinforced concrete columns?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free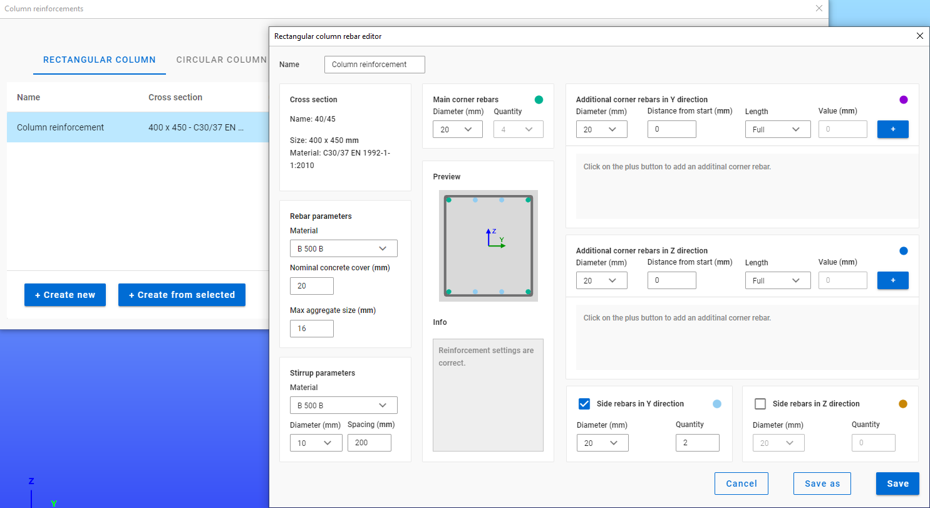
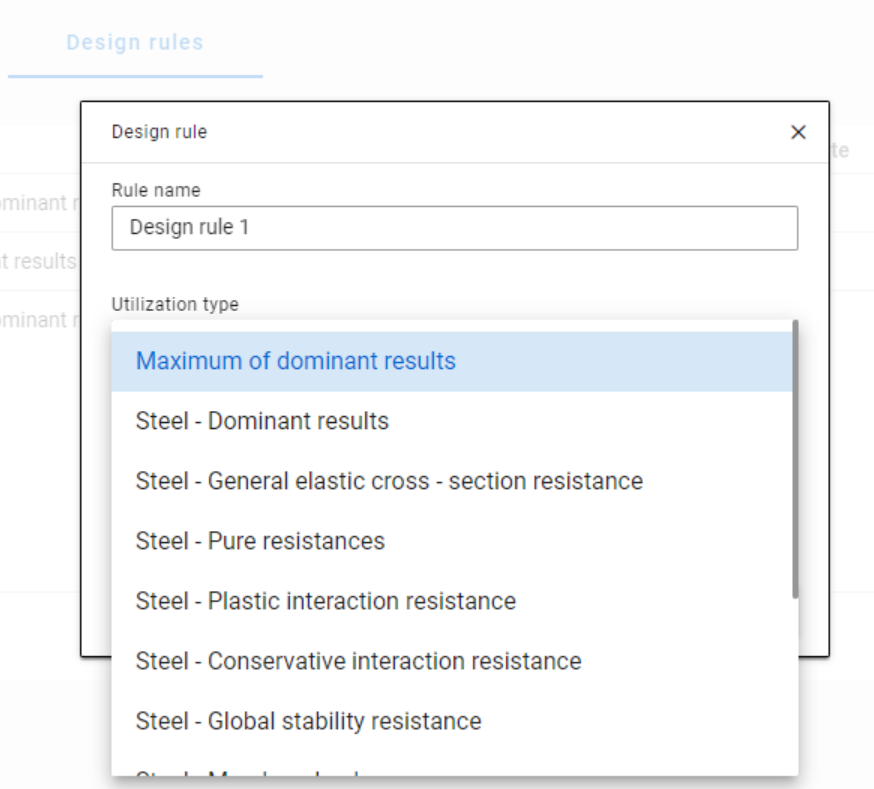
When applying design rules in load combination filter, the most frequently used utilization type is Steel – Dominant results. What results are exactly considered by this option and what do corresponding limitations mean?
Introduction
There are four ways to apply load combination filter: based on limit states and load cases, manually, and by rules. Unlike the other three methods, filter by rules is only possible based on analysis and/or design results.
The most effective way to reduce the number of load combinations is definitely the use of design rules.
With design rules, load combinations can be selected based on utility ratios. Utilizations are available from several design checks, including dominant results and detailed verifications for steel elements, such as general elastic cross-section check, pure resistances, interactions, and global stability.
The meaning of the dominant check
The dominant check is not always the check which gives the maximal ratio but the one with the maximum RELEVANT ratio. Typical example: if plastic interaction formulas are valid, those results will be dominant over general elastic cross-section check results, although the latter are higher.
Steel – Dominant results
Steel – Dominant results option contains the utility ratio of the dominant check at every finite element node, in all load combinations. Meaning that there are as many utilization values as the number of load combinations calculated, in every FE node.
It is also important to understand the difference between the utilizations of Maximum of dominant results and Steel -Dominant results. Maximum of dominant results option contains the dominant utility ratio of the dominant load combination at every node, like an envelope of Steel-Dominant results. Meaning there is only one utilization value in every FE node. Also, it is the same as the dominant result table on Global checks tab.
When a rule is applied, the utilizations of the chosen utilization type are compared against the limitation. The load combinations which give the results that correspond to the limitation, are selected by the rule. Every FE node of the selected model portion is examined.
Limitations in case of Steel – Dominant results
- Maximum: to select the combinations which cause the maximum utilization at any node. It can be the same as Maximum of dominant results, except if there are combinations where the utilization is the same and it is maximal. In this case, here all the combinations are selected, while with Maximum of dominant results, there is always one maximum.
- More than % of maximum: to select the combinations as in ’Maximum’ plus those which cause utilization that is more than the given percentage of the maximum. E.g. at a certain point max utility ratio is 80%, Limitation= More than 90% of maximum. This rule will select all the load combinations which cause utility ratios between 0,9*80=72% and 80%.
- More than: to select the combinations which cause utilization more than the defined value at any point.
Let’s see an example of a simple 2D frame for better explanation. Right-side beam is in the portion for which three design rules were applied. Five points are selected for representation but of course all the nodes of the portion are examined against the rules’ limitations.
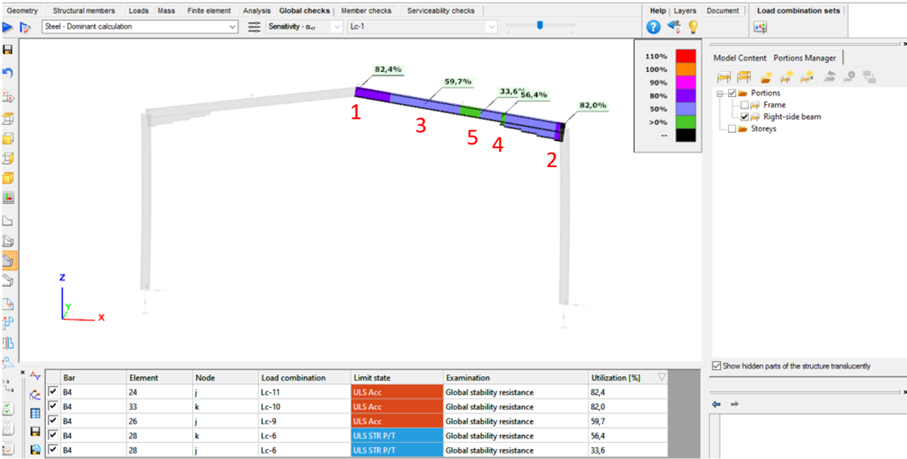
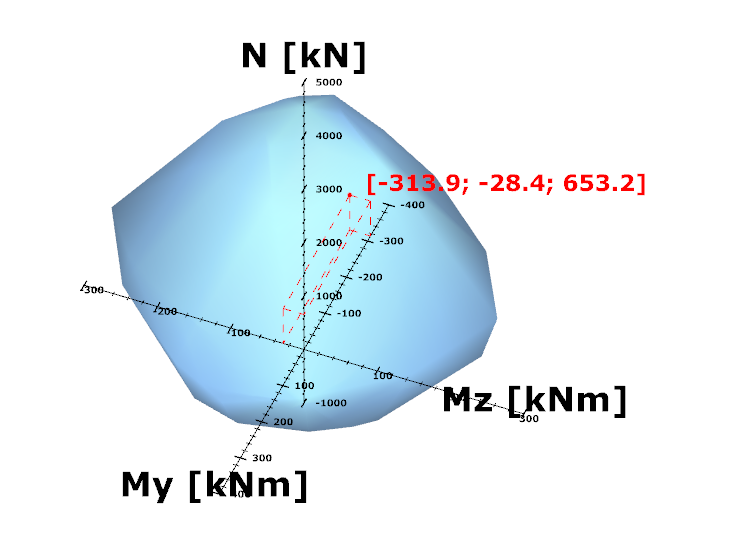
The utilizations of the five dedicated FE node in all 11 load combinations are shown on the below diagram. (To find all of these utilizations in the attached model, global checks must be calculated for the load combinations one-by-one.)
gateIntroduction
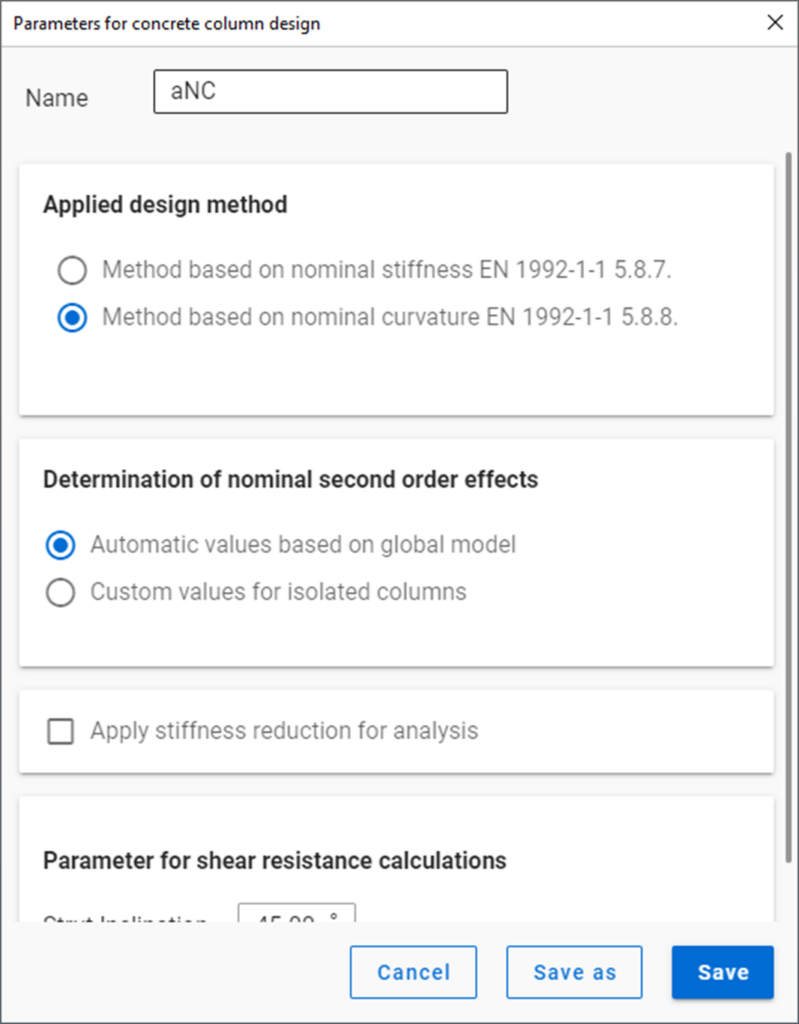
In ConSteel, there are three options for designing reinforced concrete columns: the Manual Nominal Curvature Method, the Automatic Nominal Curvature Method, and the Nominal Stiffness Method.
Each method has its advantages and disadvantages and should be used in different situations. We will now briefly review these methods and show how they can be used. Example models and a flowchart guide is also available at the end of the overview.
You can find the related chapters within the Online Manual about how to access these features in the Structural design and Structural modeling chapters.
Summary table
The following table summarizes the most important information about the three methods. Click on the table to see it in full screen.
We will now illustrate the application of these methods with a few short examples.
Examples
Manual Nominal Curvature Method
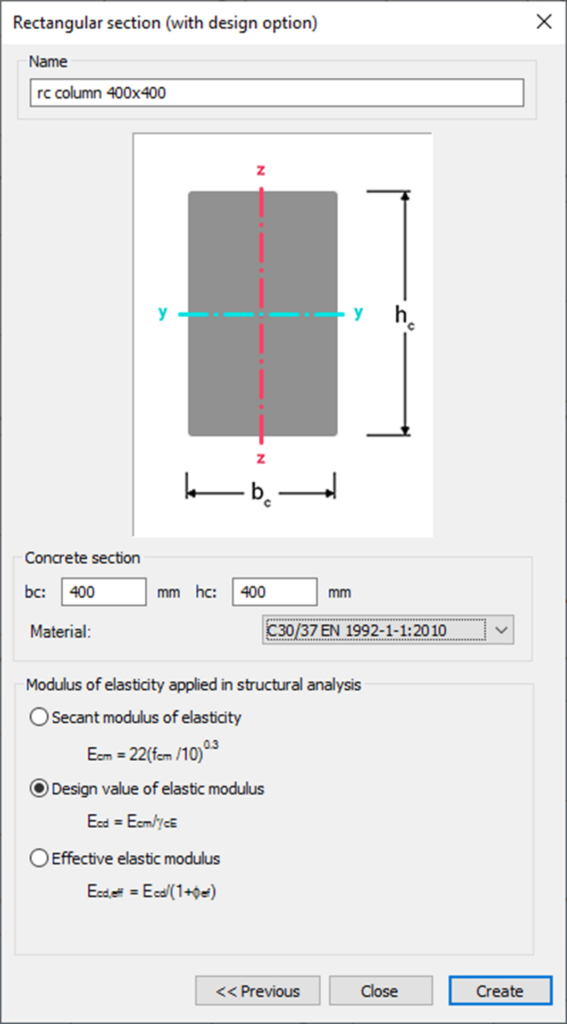
Create section
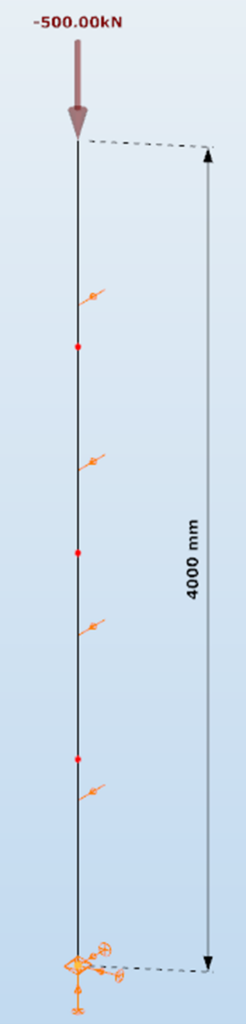
Define structure without imperfections
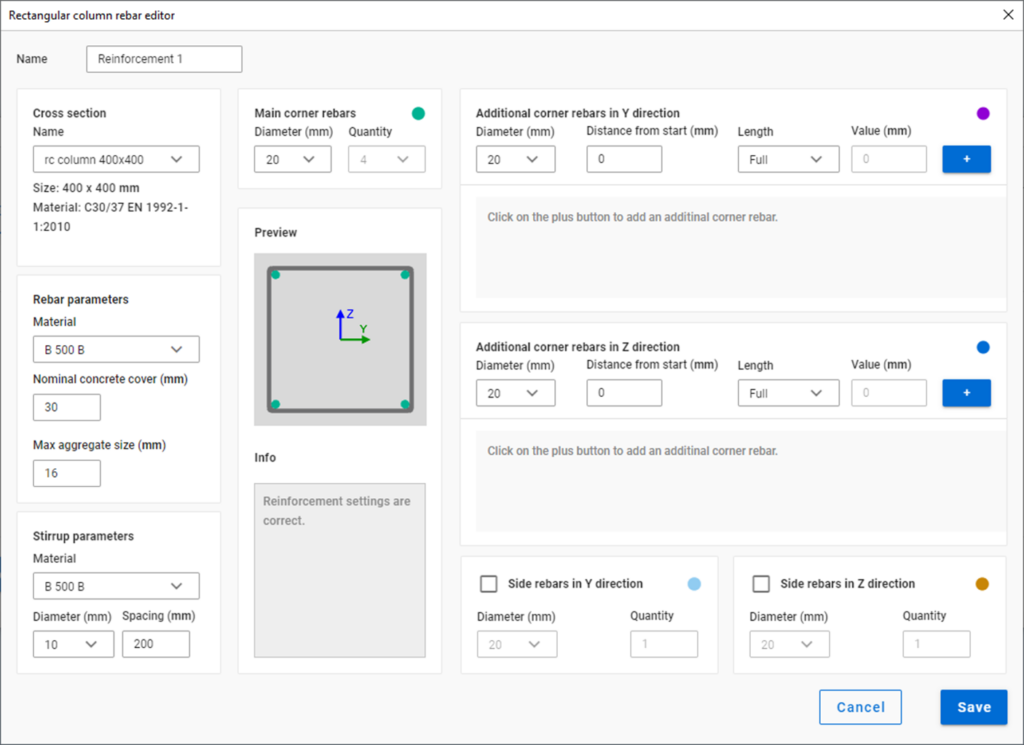
Define reinforcement
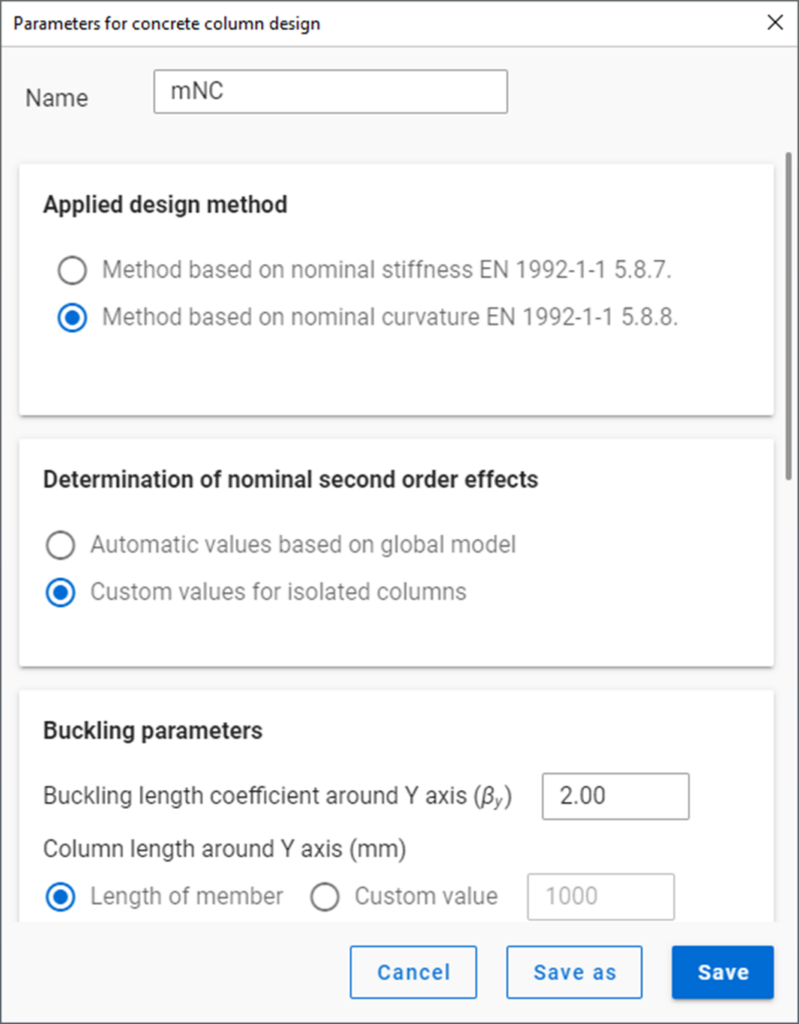
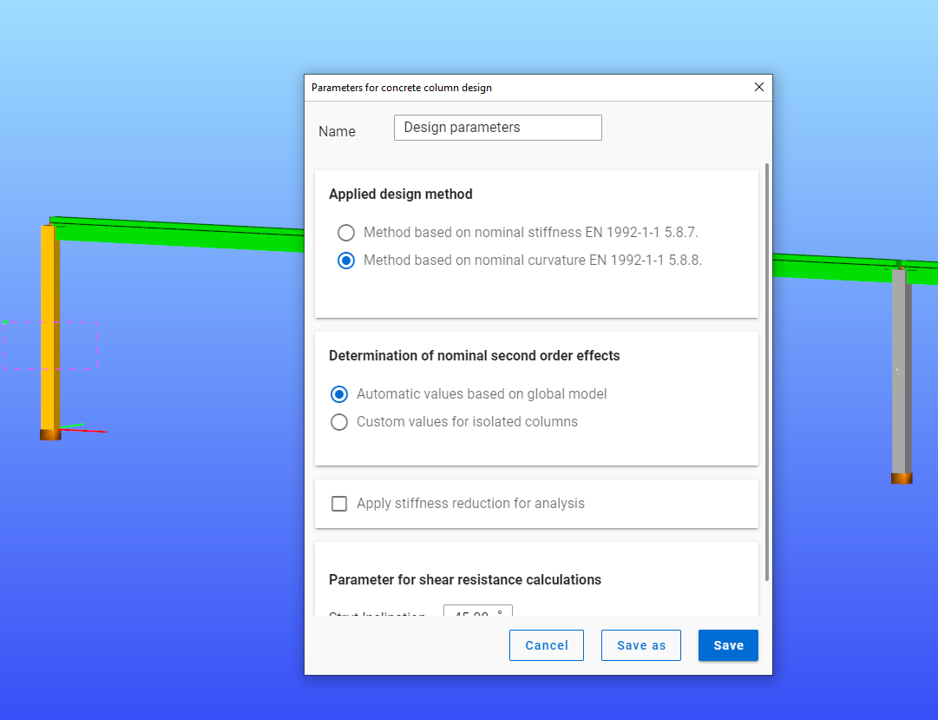
Define design parameters
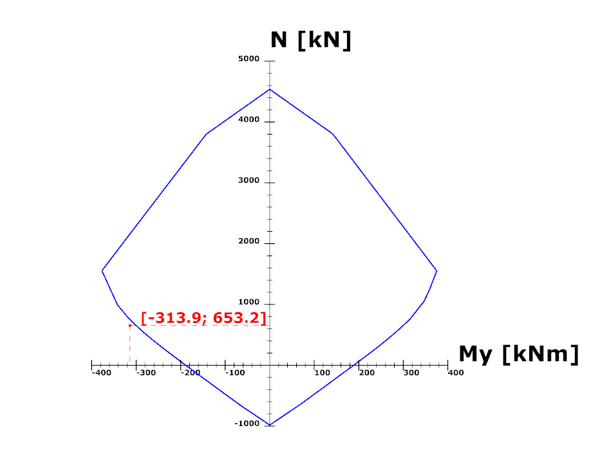
First order analysis
Design
Automatic Nominal Curvature Method
Only the steps presented, which are different from the Manual Nominal Curvature Method.
Imperfections
Design parameters
First order analysis – with imperfections
gate