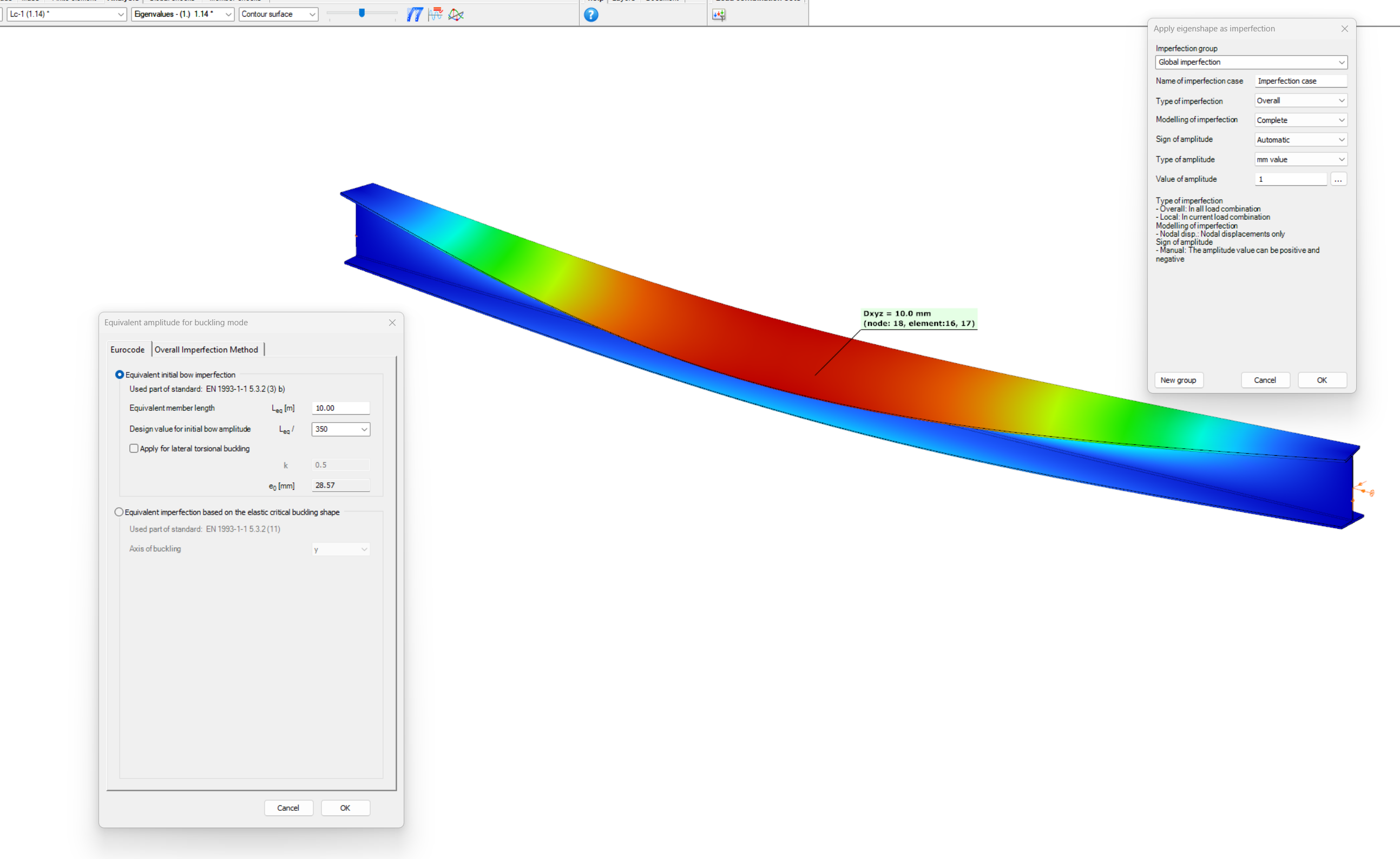
Consteel recommends to use the General Method from EN 1993-1-1 for the evaluation of out-of-plane strength of members and sturctures. In addition, the scaled imperfection based 2nd order approach is available.

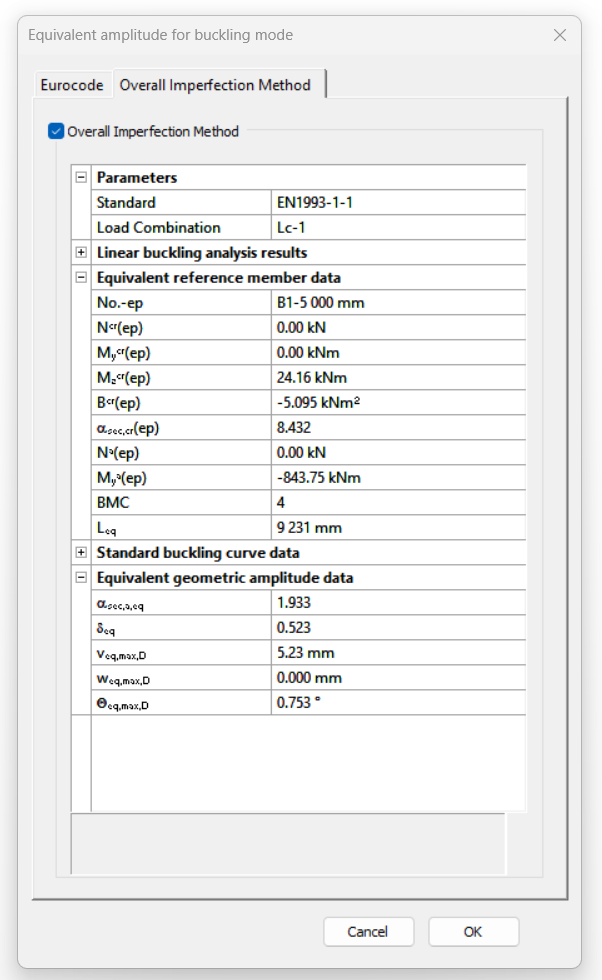
Did you know, that when linear buckling eigenform affine imperfections are used, Consteel can scale automatically the selected eigenmodes to perform a Eurocode compatible design? And you can even combine several imperfections?

Download the example model and try it!

Bending:

Download model

Copmression:

Download model

If you haven’t tried Consteel yet, request a trial for free!

Try Consteel for free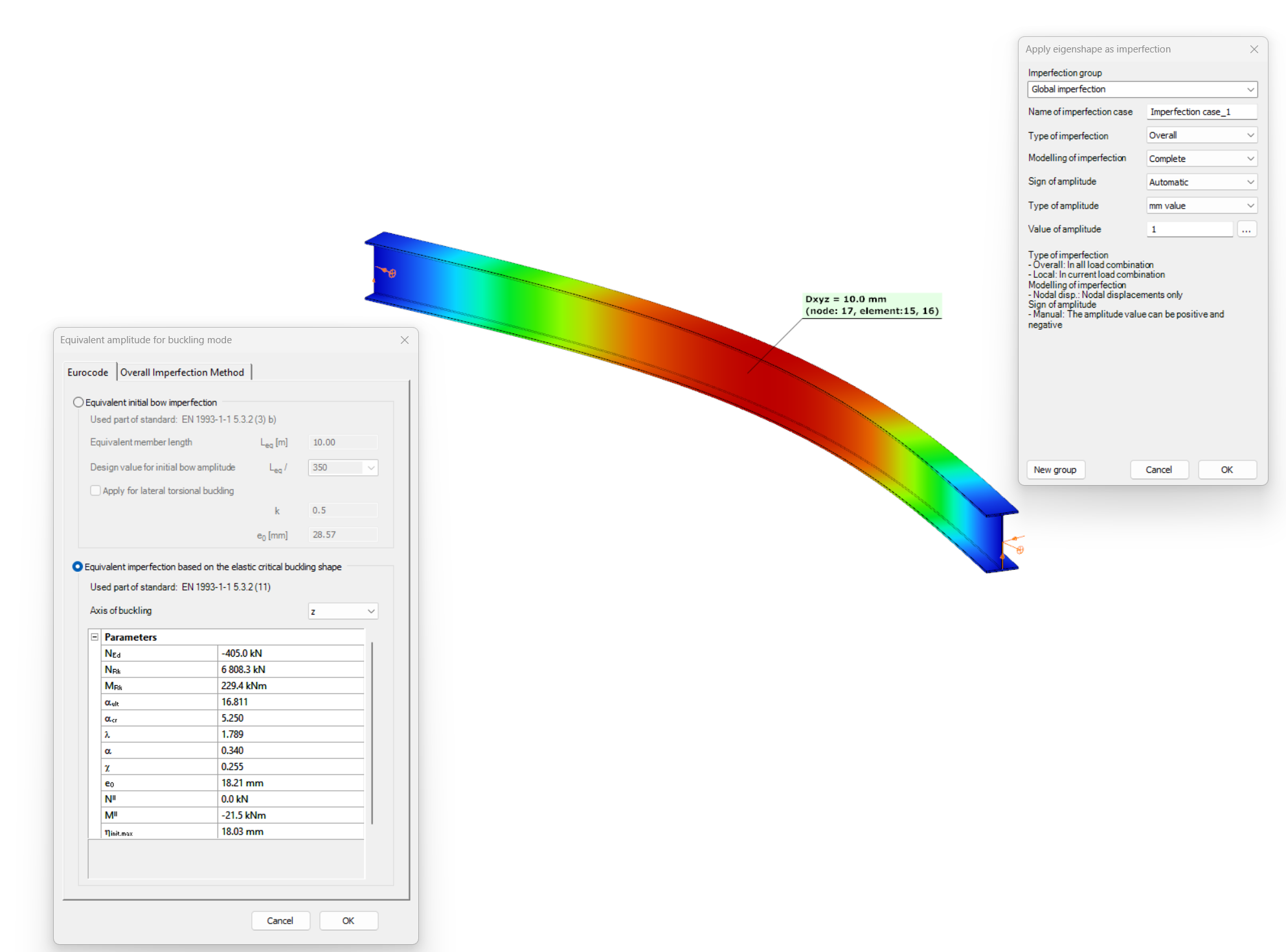

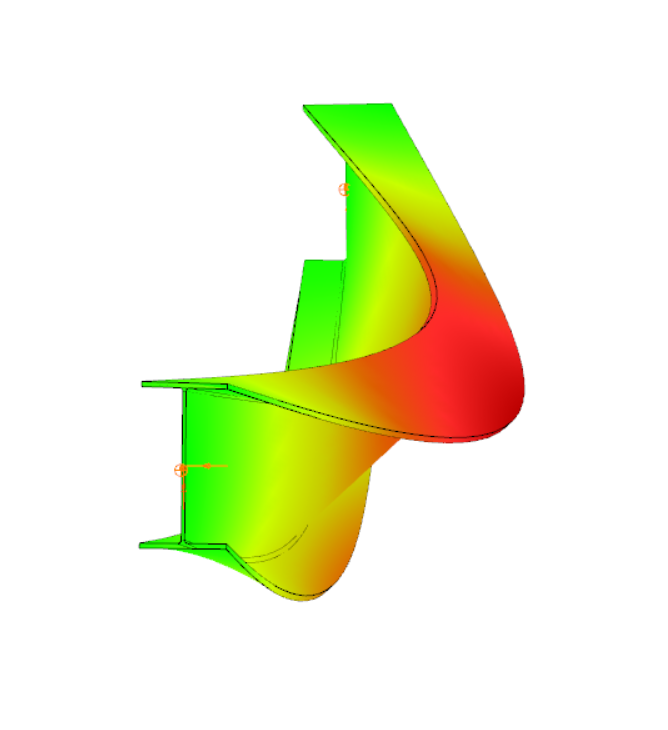
Have you ever heard about the ‘General Method’? This is an alternative design method to consider the interaction of axial compression with major-axis bending for general buckling situations, where the main interaction formulas are not applicable.

This basically includes every member with monosymmetric or asymmetric cross-sections or with cross-sections not uniform along the length (welded tapered sections) or laterally stabilized by sheeting or anything else without providing full fork supports.

Did you know, that the General Method is fully supported by Consteel and provides an automated buckling verification possibility? Of course, for the use of the General Method in a general case the traditional 12DOF beam finite elements are not applicable. But the special 14DOF beam elements used by Consteel are perfectly compatible? 

Download the example model and try it!

Download model

If you haven’t tried Consteel yet, request a trial for free!

Try Consteel for free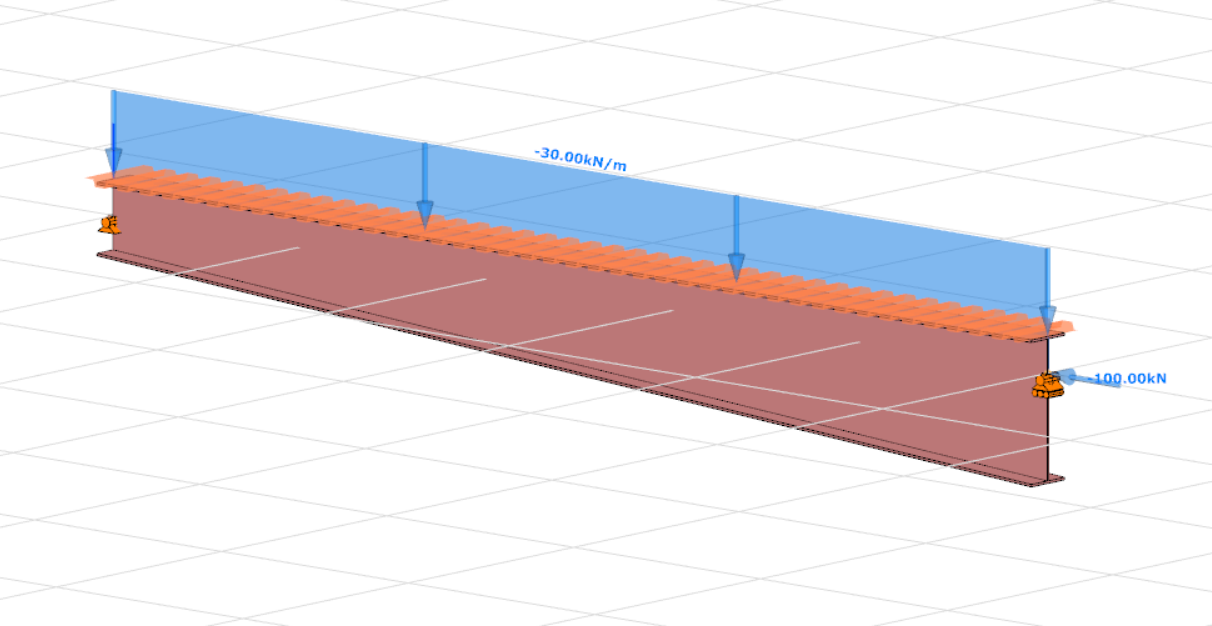

Introduction

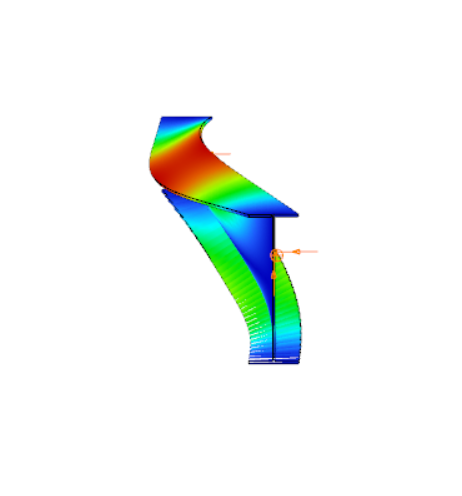
When a beam, bent in a plane, is allowed to move and twist freely between its two support points, in addition to bending, sudden perpendicular displacement and twisting may occur: causing the beam to deviate out of its original plane. This phenomenon is illustrated in Figure 1, showing a single supported beam with I-section bent around the strong axis. As the bending moment in the vertical plane increases, reaching a critical value, the beam undergoes abrupt lateral movement and twisting between the supports. This phenomenon is called lateral torsional buckling (LTB), which is a loss of stability mode that can apply to both perfect beams and real beams.

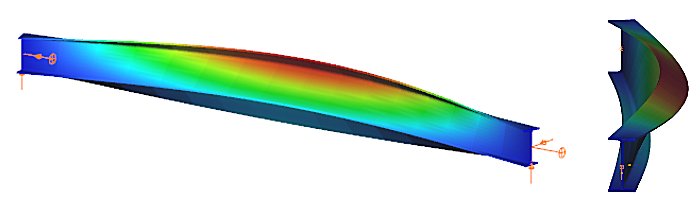
The design of the beam against LTB is fully analogous to the design of a compressed column against flexural buckling. The analogy is illustrated in Table 1, where the corresponding parameters are shown that affect the two buckling resistances:

Flexural (column) buckling	Lateral torsional buckling
design force ($N_{Ed}$)	design moment ($M_{Ed}$)
critical force ($N_{cr}$)	critical moment ($M_{cr}$)
column slenderness ($\frac{}{\lambda}$)	beam slenderness ($\frac{}{\lambda}_{LT}$)
buckling reduction factor ($\chi$)	buckling reduction factor ($\chi_{LT}$)
buckling resistance ($N_{b,Rd}$)	buckling resistance ($M_{b,Rd}$)

The critical moment of the perfect beam is determined at the location of the maximum value of the M_y,Ed design bending moment diagram. For a doubly symmetrical I cross-section:

$$M_{cr}=C_1\frac{\pi^2EI_z}{(k_z⋅L)^2}\left[\frac{I_\omega }{I_z}+ \frac{(k_zL)^2GI_t}{\pi^2EI_z}\right] ^{0.5} $$

where k_z is the coefficient of restraint about the weak axis of the cross-section, G is the shear modulus, and I_t and I_ω are the pure (St. Venant) and warping torsional moments of inertia of the cross-section. The value of the factor C₁ depends on the shape of the bending moment diagram and its value can be found in appropriate tables and manuals. For a constant moment diagram, C₁=1.0. The formula for the other design parameters, in particular the buckling reduction factor $\chi_{LT}$, depends on the design standard considered.

Lateral torsional buckling resistance by EN1993-1-1  

The design of the beam against LTB (load capacity check) according to EC3-1-1 shall be carried out in the following steps:

gate

This overview delves into Consteel’s solution, offering an alternative approach to calculating effective cross-sectional properties and reshaping conventional methodologies in structural analysis and design.

Determine the strength utilization of a double symmetric welded I cross-section with 384×4 web and 300×8 flanges, if the internal forces on the cross-section are N_Ed=500kN compressive force and M_y,Ed=100kNm bending moment. The material grade of the cross section is S235.

Calculation of cross-sectional properties

First, take the cross-section data (symmetric welded I-section), from which the Consteel software generates the EPS (and GSS) (see Online Manual/10.1.1 The EPS model) cross-section model (Fig. 1).

If the cross-section is class 4, the effective model is determined by the assumed normal stress distribution. According to EC3-1-1, the EPS model of a class 4 cross-section can be defined in two ways :

– method A: based on pure stress conditions,

– method B: based on complex stress condition.

In order to compare the results, the cross-section properties will be calculated by method A at first and then by method B.

Cross-sectional properties by method A

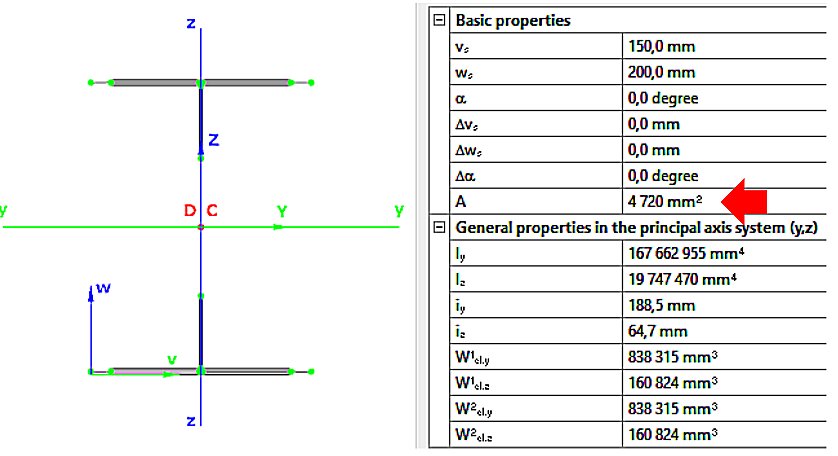
• pure compression N_Ed  (Fig. 2): 

A_eff=4720mm²   

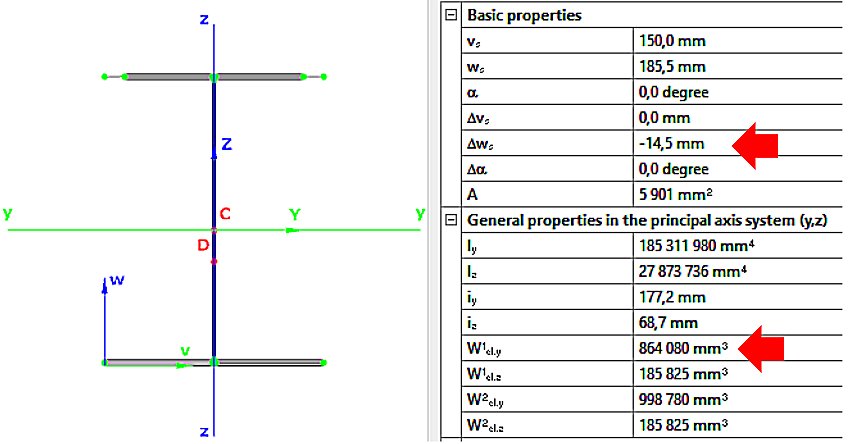
• pure bending M_y,Ed  (Fig. 3): 

W_eff,y,min=864080mm³

e_z=14.5mm 

Cross-sectional properties by method B

GATE

In Consteel, the calculation of cross sectional interaction resistance for Class 3 and 4 sections is executed with the modified Formula 6.2 of EN 1993-1-1 with the consideration of warping and altering signs of component resistances. Let’s see how…

Application of EN 1993-1-1 formula 6.2

For calculation of the resistance of a cross section subjected to combination of internal forces and bending moments, EN 1993-1-1 allows the usage -as a conservative approximation- a linear summation of the utilization ratios for each stress resultant, specified in formula 6.2.  

$$\frac{N_{Ed}}{N_{Rd}}+\frac{M_{y,Ed}}{M_{y,Rd}}+\frac{M_{z,Ed}}{M_{z,Rd}}\leq 1$$

As Consteel uses the 7DOF finite element and so it is capable of calulcating bimoment, an extended form of the formula is used for interaction resistance calculation to consider the additional effect.

$$\frac{N_{Ed}}{N_{Rd}}+\frac{M_{y,Ed}}{M_{y,Rd}}+\frac{M_{z,Ed}}{M_{z,Rd}}+\frac{B_{Ed}}{B_{Rd}}\leq 1$$

Formula 6.2 ignores the fact that not every component results the highest stress at the same critical point of the cross-section.

In order to moderate this conservatism of the formula, Consteel applies a modified method for class 3 and 4 sections. Instead of calculating the maximal ratio for every force component using the minimal section moduli (W), Consteel finds the most critical point of the cross-section first (based on the sum of different normal stress components) and calculates the component ratios using the W values determined for this critical point. Summation is done with considering the sign of the stresses caused by the components corresponding to the sign of the dominant stress in the critical point.

(For class 1 and 2 sections, the complex plastic stress distribution cannot be determined by the software. The Formula 6.2 is used with the extension of bimoments to calculate interaction resistance, but no modification with altering signs is applied)

Example

Let’s see an example for better explanation.

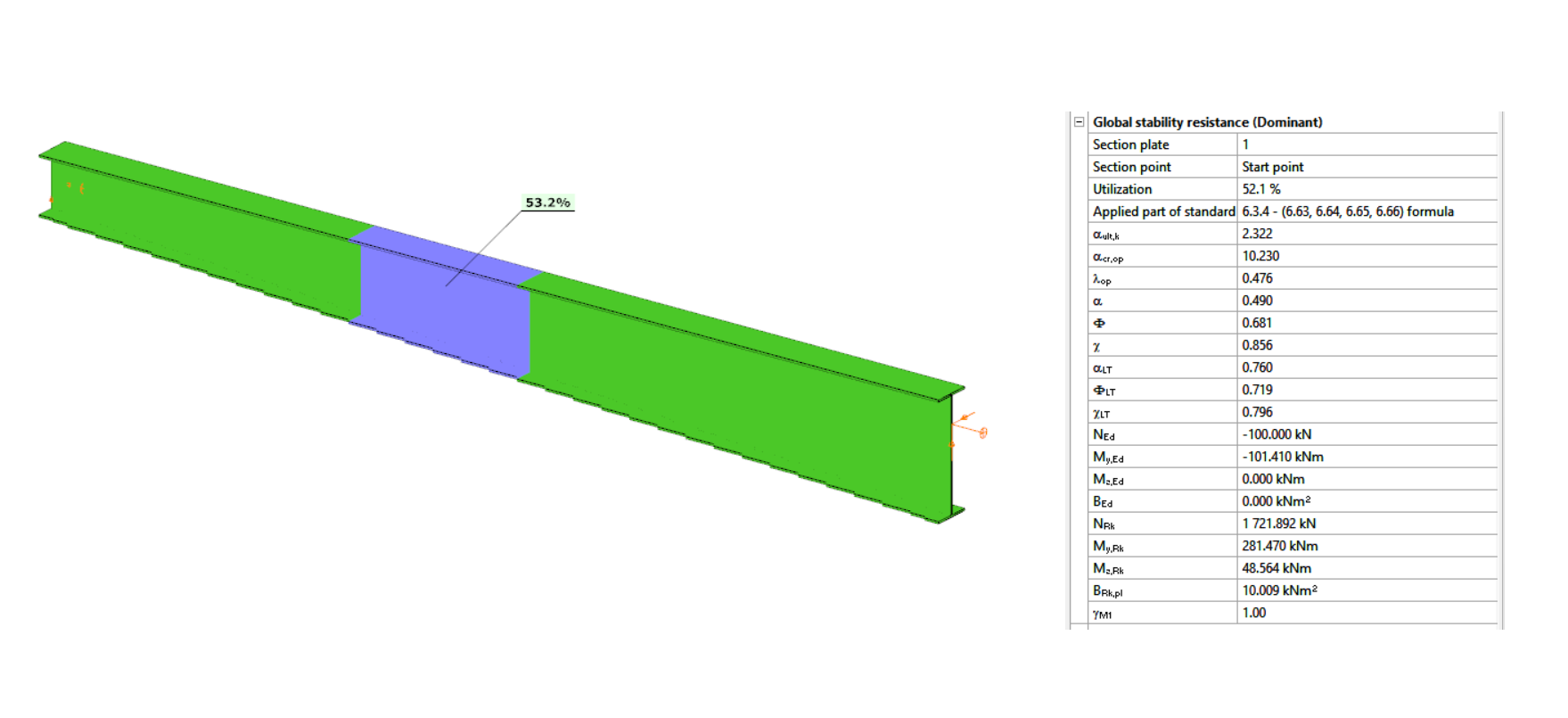
GATE

The practical use of the ‘General method’ of EN 1993-1-1 6.3.4 for the buckling design of global structural models is still a challenging issue requiring several problems to solve. In this paper we propose a fully developed methodology presenting solutions for the application topics such as the suitable FE model, specific modeling issues to capture the true 3D behavior of the members and the whole model and the final evaluation of the design parameters. The presented methodology consistently uses a unique model for the evaluation of all analysis and design parameters and results and yields a fully automatic design process controlled solely by the properly created structural model.

Click the button bellow to download and read the full article.

gate