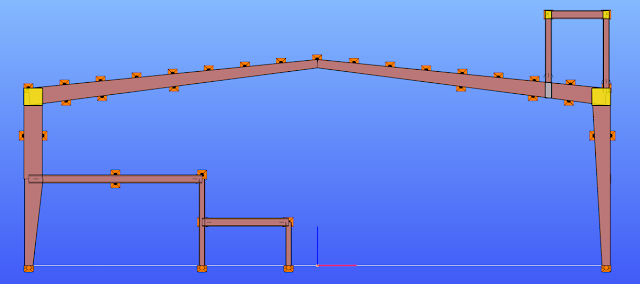
In everyday practice frames of pre-engineered metal buildings are often designed as 2D structures. Industrial buildings often have partial mezzanine floors, attached to one of the main columns, to suit the technology. Additionally, such buildings often have above the roof platforms for machineries.
When it comes to seismic design, as long as seismicity is not deemed to be a strongly controlling factor for final design, the mezzanines are just attached to the same type of frames as used at other non-seismic locations and are locally strengthened, if necessary. Only the horizontal component of the seismic effect is considered in most of the cases.
The following picture shows a typical intermediate frame of a longer industrial hall, with built-in partial mezzanine floor and with a platform placed above the roof.
Equivalent Lateral Force method
The most straightforward design approach is the Equivalent Lateral Force (ELF) method (EN 1998-1 4.3.2.2). There are certain conditions for the application of this method.
- (1)P. this method may be applied to buildings whose response is not significantly affected by contributions from modes of vibration higher than the fundamental mode in each principal direction
- (2) the requirement in (1)P is deemed to be satisfied in buildings which fulfill both of the following conditions
o they have a fundamental period of vibration smaller than the followings
4*Tc or 2.0 sec
o they meet the criteria for regularity in elevation given in 4.2.3.3
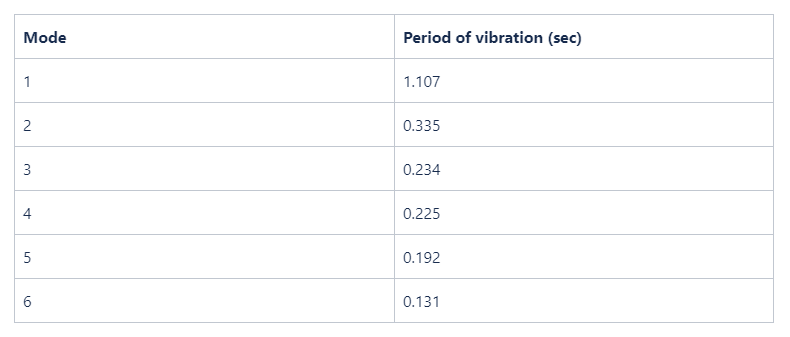
When a dynamic analysis is performed on this 2D frame, the following vibration modes are obtained:
The first condition is met, but the criteria for the regularity in elevation is difficult to be judged. The first condition of 4.2.3.3(2) is met, but 4.2.3.3(3) is not really, as the mass is not decreasing gradually from foundation to the top, because of the heavily loaded above the roof platform.
Let us disregard for a moment this second criteria and accept the ELF method.
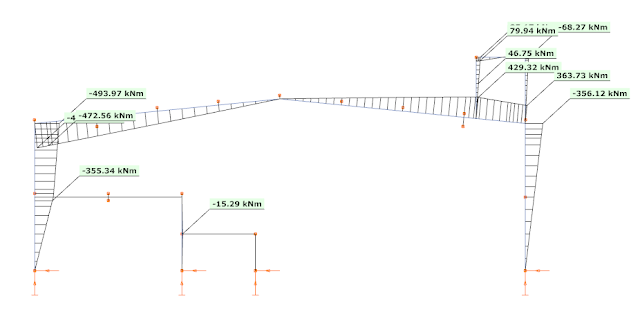
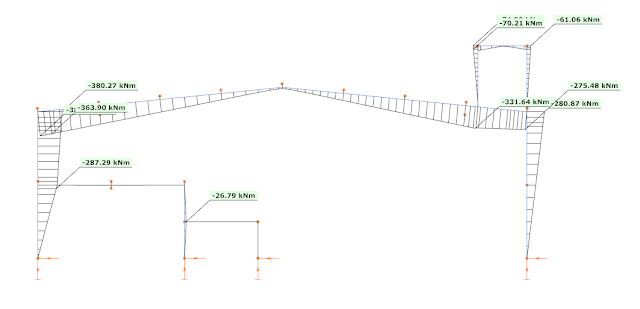
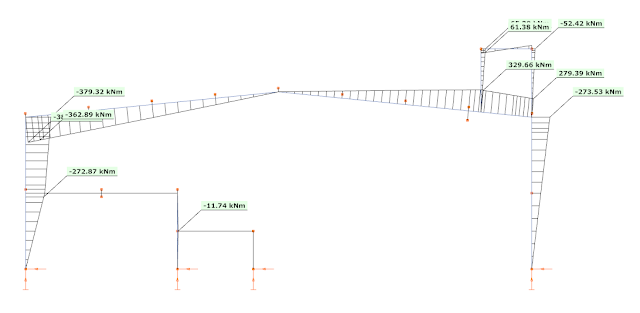
When the ELF method is applied, only the first (fundamental) mode is used, with the total seismic mass of the building carried by this frame. As the seismic effect is described with one single fundamental vibration mode only, the representation of the seismic effect is a simple equivalent load case, called as dominant load. Using this regular load case all the common first and second-order analysis can be performed, as also the linear buckling analysis. For example, the bending moment diagram calculated from the dominant mode (from left to right) is the following:
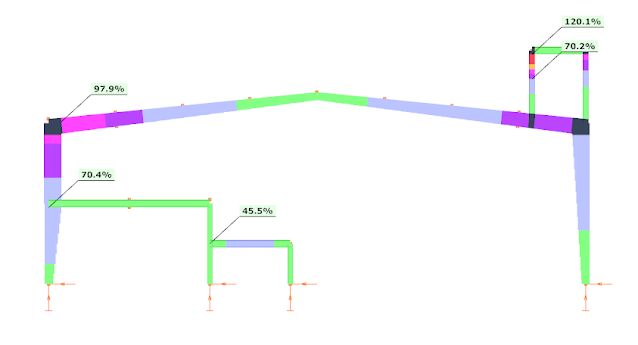
This way Consteel can perform an automatic strength and stability verification for the seismic combinations. The results are visible here, respectively:
As it can be seen the structure is generally OK for strength, but there are some local overstresses at the platform and the utilization ratio is very high at the left corner. Regarding stability verifications the section seem to be weak. So – as expected – it is a key importance to be able to perform the stability verifications.
Of course, the platform column could be strengthened and close this exercise. But somebody can still have some doubts about the applicability of this ELF method, due to the criteria of vertical regularity.
Modal Response Spectrum Analysis
How could this structure be more precisely calculated? The general approach proposed by EN 1998 is the Modal Response Spectrum Analysis (MRSA) (EN 1998-1 4.3.3.3). This method is applicable in all cases, where the fundamental mode of vibration alone does not describe adequately the dynamic response of the structure. MRSA will take into account all the calculated vibration modes, not only the fundamental and therefore the precise seismic effect can be worked out on the structure. But the main problem is that this will result an envelope of the maximum values of internal forces and displacements, without any guarantee that these correspond to the same time frame of the seismic action. Plus, the internal forces produced at ends of members connected to a given node are not even in static equilibrium…. And even the sign of the internal forces or deformations is only positive due to the use of modal combinations SRSS or CQC. And even worse, as the seismic action calculated this way cannot be described by a single load case or by a linear combination of multiple load cases, no linear buckling analysis can be performed and therefore the automatic buckling feature of CosSteel cannot be used.
Let us see what MRSA with a CQC combination would give.
The first 7 vibration modes with the corresponding seismic mass participation values can be seen in the next table. The first column shows the frequencies in Hz and the second column shows the mass contribution factors in the horizontal direction. The other columns mean the mass participation in the other directions (out-of-plane and vertical), but these are not important for our example.
EN 1998 requires to consider enough vibration modes in each direction to reach a minimum of 90% of the seismic mass.
With Consteel the first 7 vibration modes have been calcualated and the results are shown in the table. Direction ‘1′ means horizontal in-plane direction while ‘2’ means horizontal out-of-plane direction and ‘z’ means the vertical direction. We are concentrating now on the vibrations which happen in the plane of this frame.
As visible, the fundamental mode has high contribution (77%) but does not reach the required level. The difference may justify the initial doubts about only using this single mode and disregard all the others. To fulfill the 90% minimum criteria, the second mode (17%) must be also considered, but visible even the 4th and the 6th have non-zero (although less then 5%) contributions in this direction.
As said before Consteel can perform only strength verifications but no stability verifications based on results obtained from an MRSA combined with CQC modal combination rule.
The bending moment diagram with the maximum possible values looks as shown below (all the bending moment values from the multimodal result are without a sign, they must be assumed as positive and negative values as well):
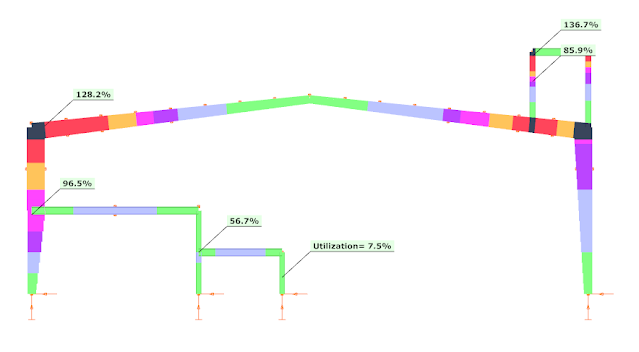
The results of the strength verification are the following:
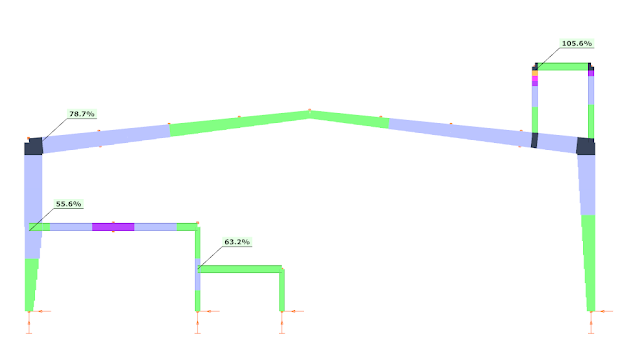
As visible the platform leg is still weak, it must be strengthened without a question. On other hand the utilization ratio (without stability verification!!) at the left corner is lower, therefore there is a chance the the ELF-based 97.9% strength verification result could be still acceptable as safe, but the stability must be checked somehow.
But it is also visible, that generally the bending moments obtained by MRSA CQC are much lower than those obtained with the ELF method. Why is this? And how can a stability verification be performed?
Consteel approach
Seismic modal analysis with “selected modes”
Luckily Consteel provides a very flexible approach, called as „selected modes” method. This allows the user to pick the vibration modes and create linear combinations from them by specifying appropriate weighting factors. As a result, a linear combination of the modal loads calculated from vibration modes is obtained, instead of the quadratic SRSS or CQC combinations, which can be considered already as a single equivalent load case and all the necessary first- and second-order static and linear buckling analysis can be performed, as in the case of ELF calculation.
The definition of the „selected modes” and the specification of weighting factor is not an automated process in Consteel, it must be driven by the user. To be successful, it is important to understand how the structure works.
Although the first 2 vibration modes together already fulfill the minimum 90% mass contribution requirement, let us see the additionally also the 4th mode:
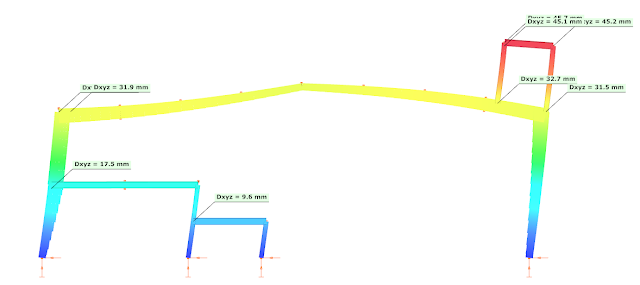
1st mode f=0.90 Hz, T=1.109 sec
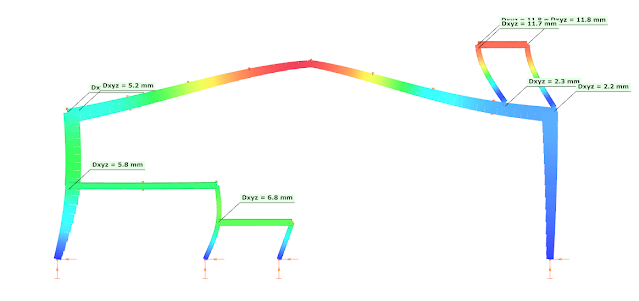
2nd mode f=3.00 Hz, T=0.334 sec
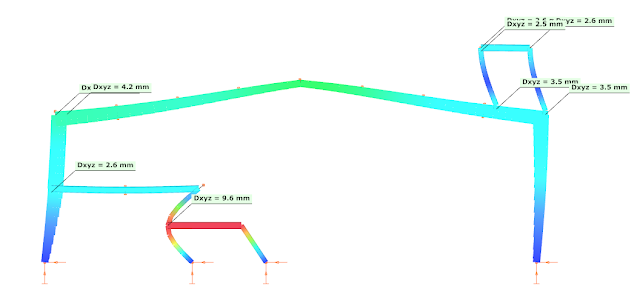
4th mode f=4.265 Hz, T=0.234 sec
The colors suggest that the fundamental mode describes globally the structure, but the second seems to affect additionally the platform region and the 2nd or 4th is dominant for the mezzanine structure.
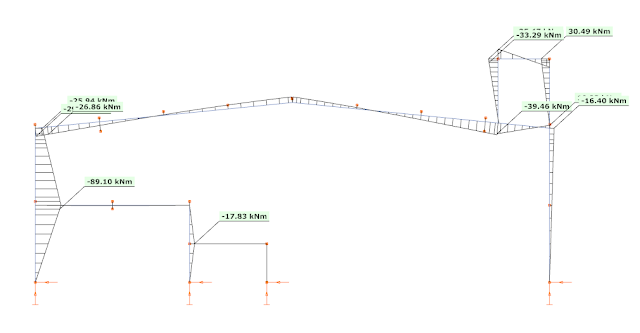
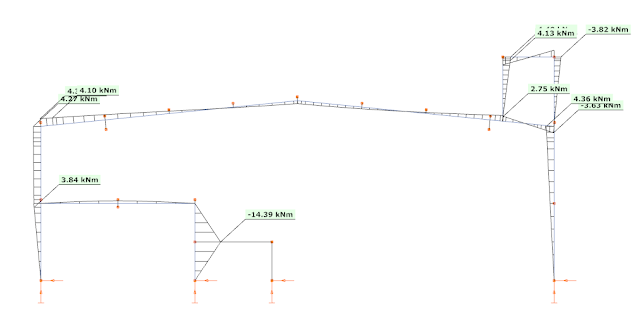
The corresponding bending moment diagrams are, respectively:
These bending moments also justify the assumption made based on the colors, the 2nd mode creates significant bending moments additionally to the first mode and the 4th mode creates significant bending moments additionally to the 1st mode. But it seems that also the 2nd mode created significant bending moments at this region.
It is interesting to note, that the bending moment diagram from the 1st mode (picture 9) almost perfectly fits to the CQC summarized bending moment (of course by assigning signs to the values based on the fundamental vibration mode) (see picture 4), except in the regions of the platform and the mezzanine. This means that in general the fundamental vibration modes describes quite well the dynamic response of this frame. And because of this, the bending moments could be calculated with the mass contribution factor corresponding to this mode (77%). And this is the reason, why the ELF method gives higher bending moment values, as there the same vibration mode was considered, but instead of the corresponding mass (77%), with 100% of the seismic mass.
As we discovered, the 2nd mode should be used together with the 1st mode to correctly describe the platform region, as this region is not fully dominated by the 1st mode only, the 2nd has a significant contribution.
Similarly to the mezzanine region, additionally to the 1st mode, here the 4th mode must be used to better approach the correct result.
gate