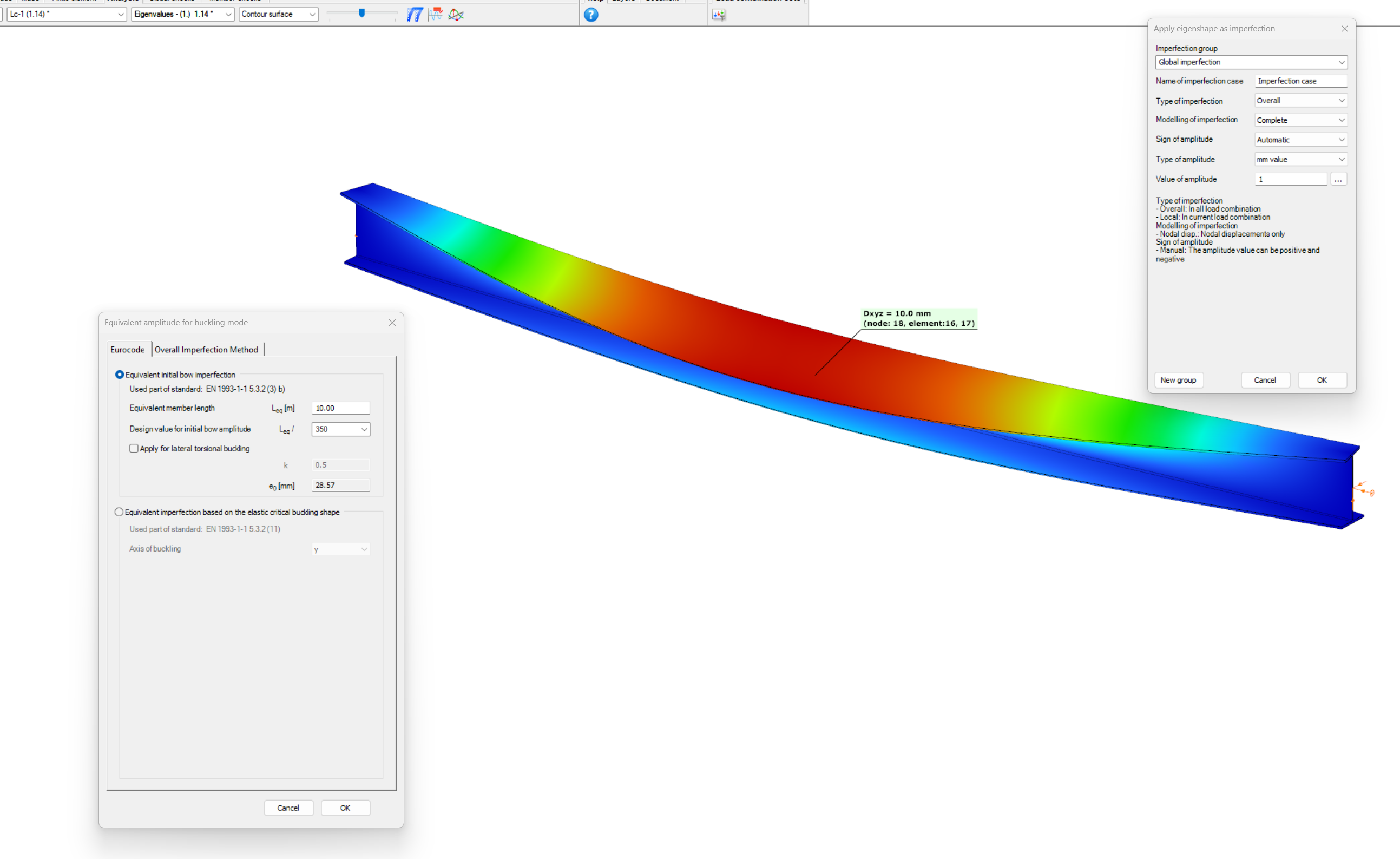
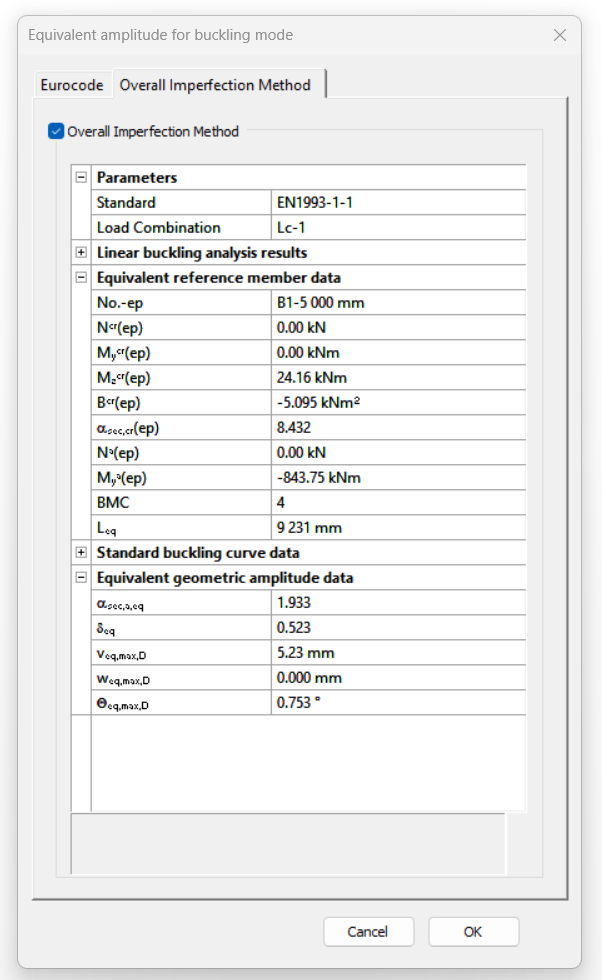
Consteel recommends to use the General Method from EN 1993-1-1 for the evaluation of out-of-plane strength of members and sturctures. In addition, the scaled imperfection based 2nd order approach is available.
Did you know, that when linear buckling eigenform affine imperfections are used, Consteel can scale automatically the selected eigenmodes to perform a Eurocode compatible design? And you can even combine several imperfections?
Download the example model and try it!
Bending:
Download modelCopmression:
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free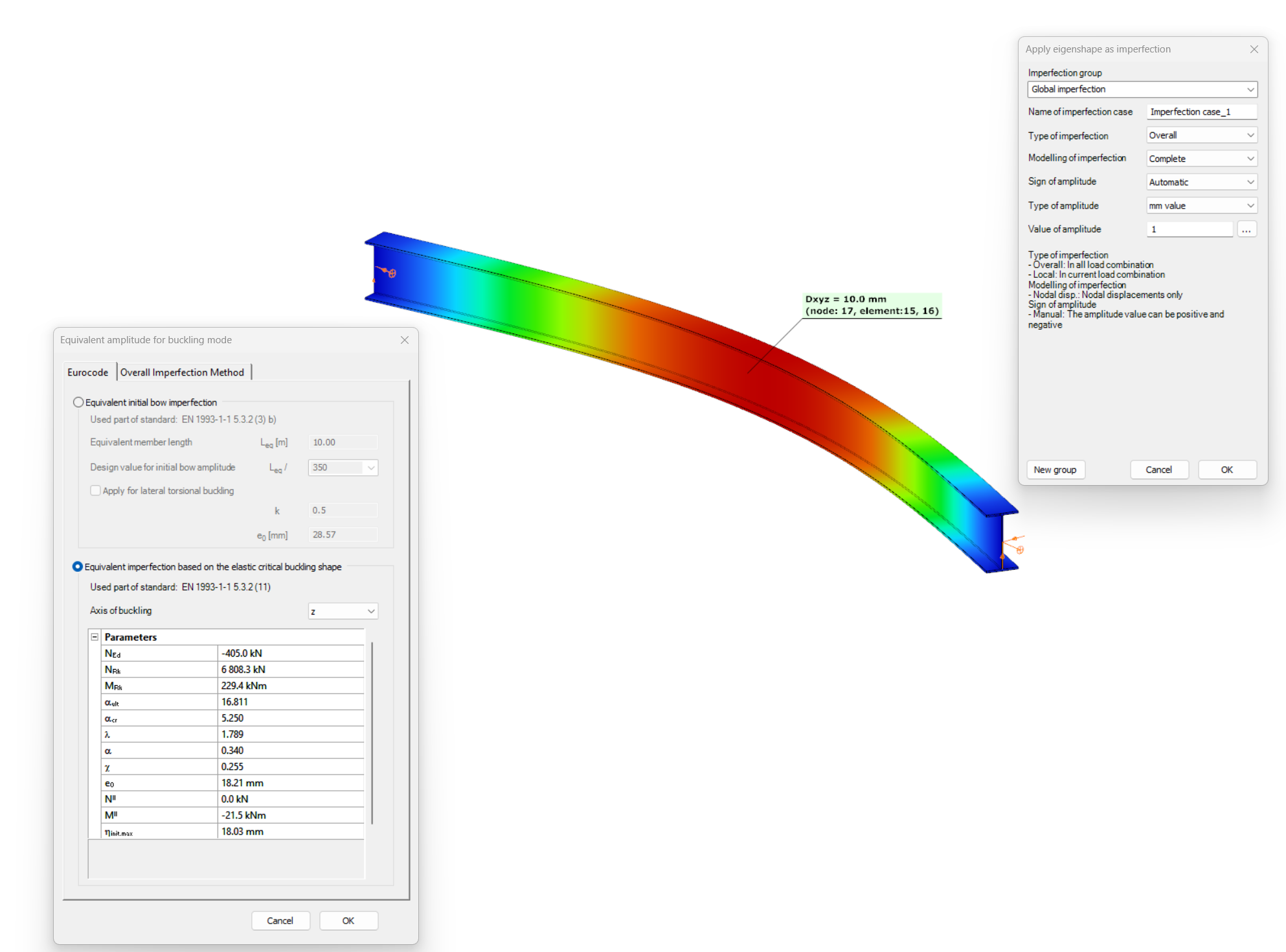
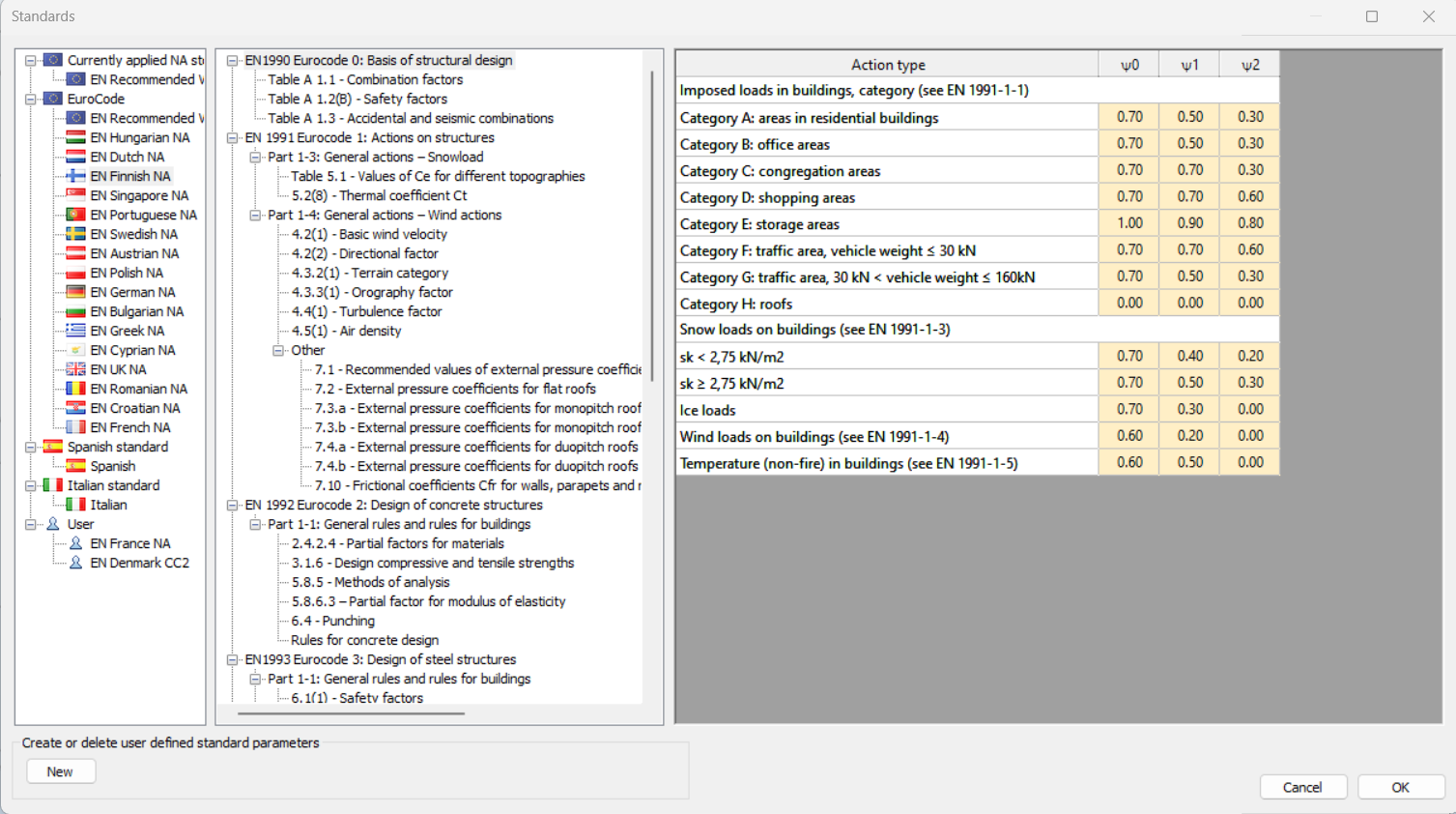
Did you know that Consteel already supports most of the countries which have adopted Eurocode design standard? If your country would still be missing, no problem, you can create your own NA settings. This is useful also in the case when you want to customize the recommended settings based on your own preference.
If you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free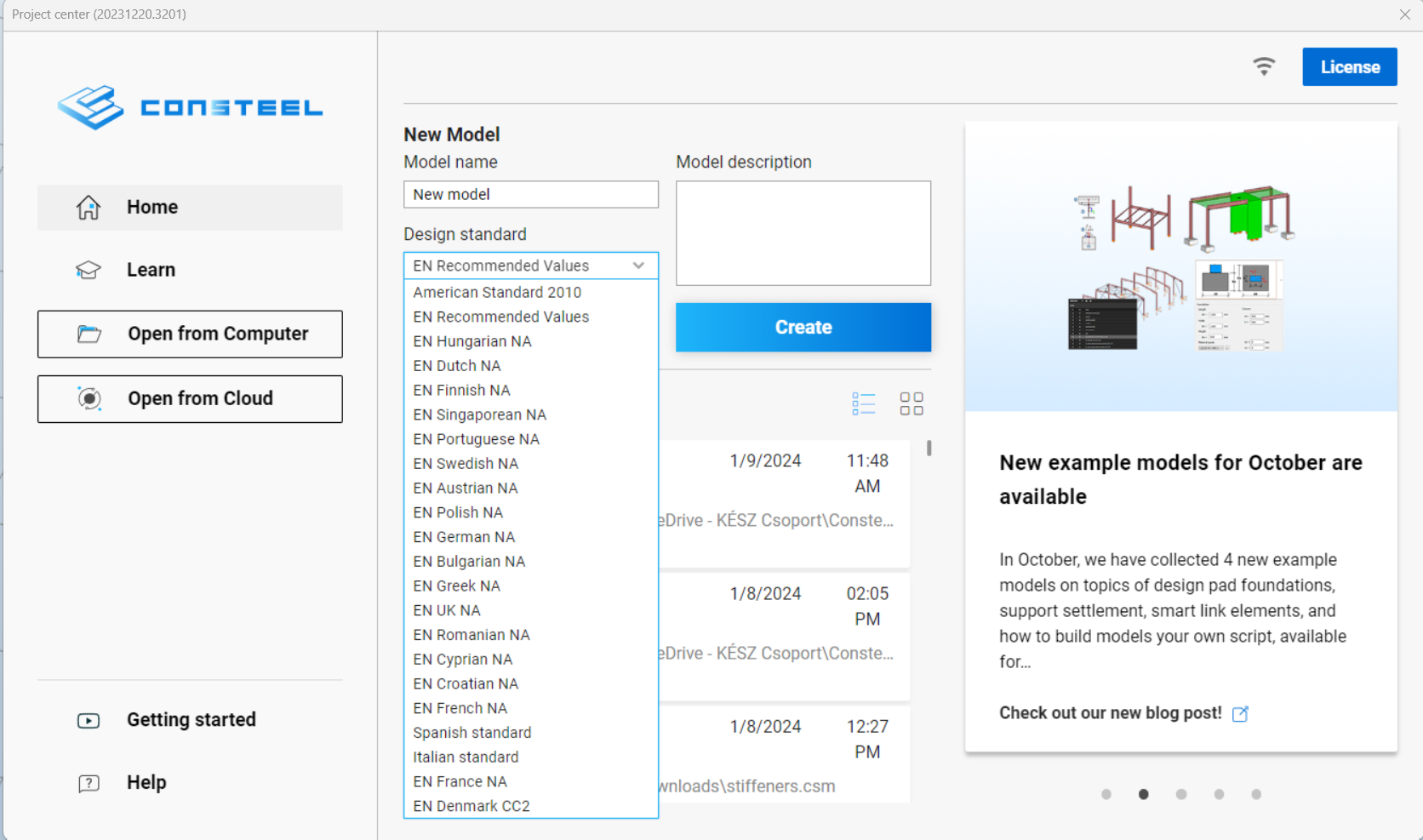

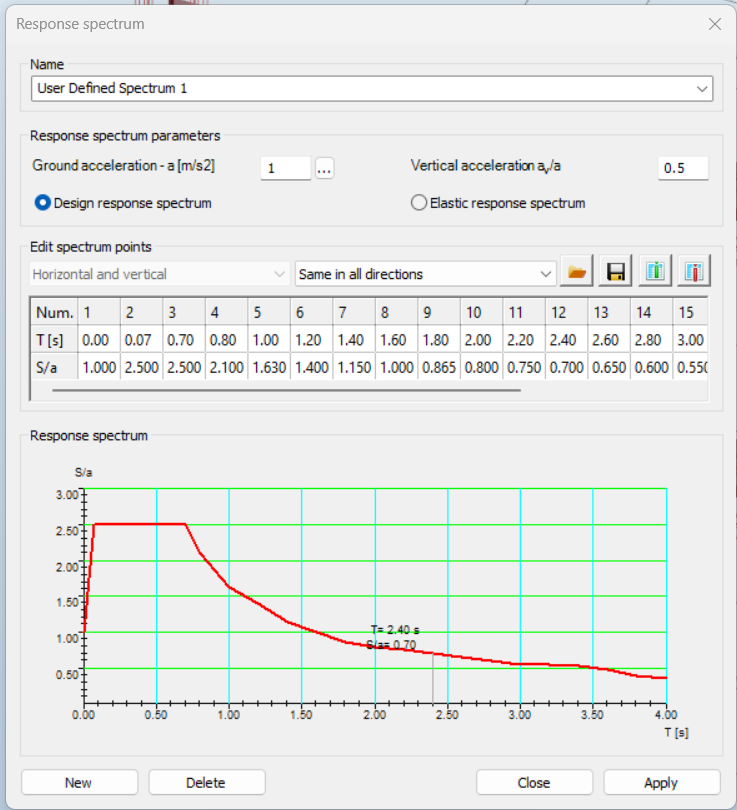
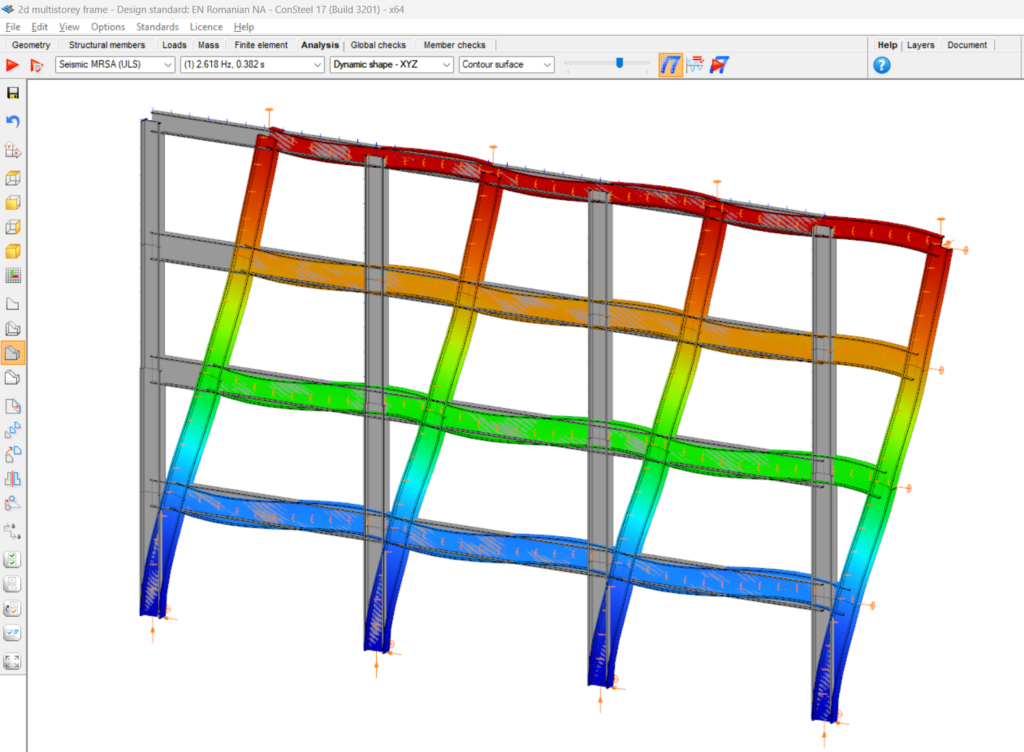
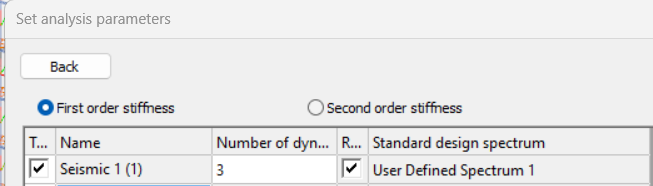
Did you know that in addition the standard Type 1 and Type 2 response spectrums defined by Eurocode 8, you can use also user-defined spectrums with Consteel?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free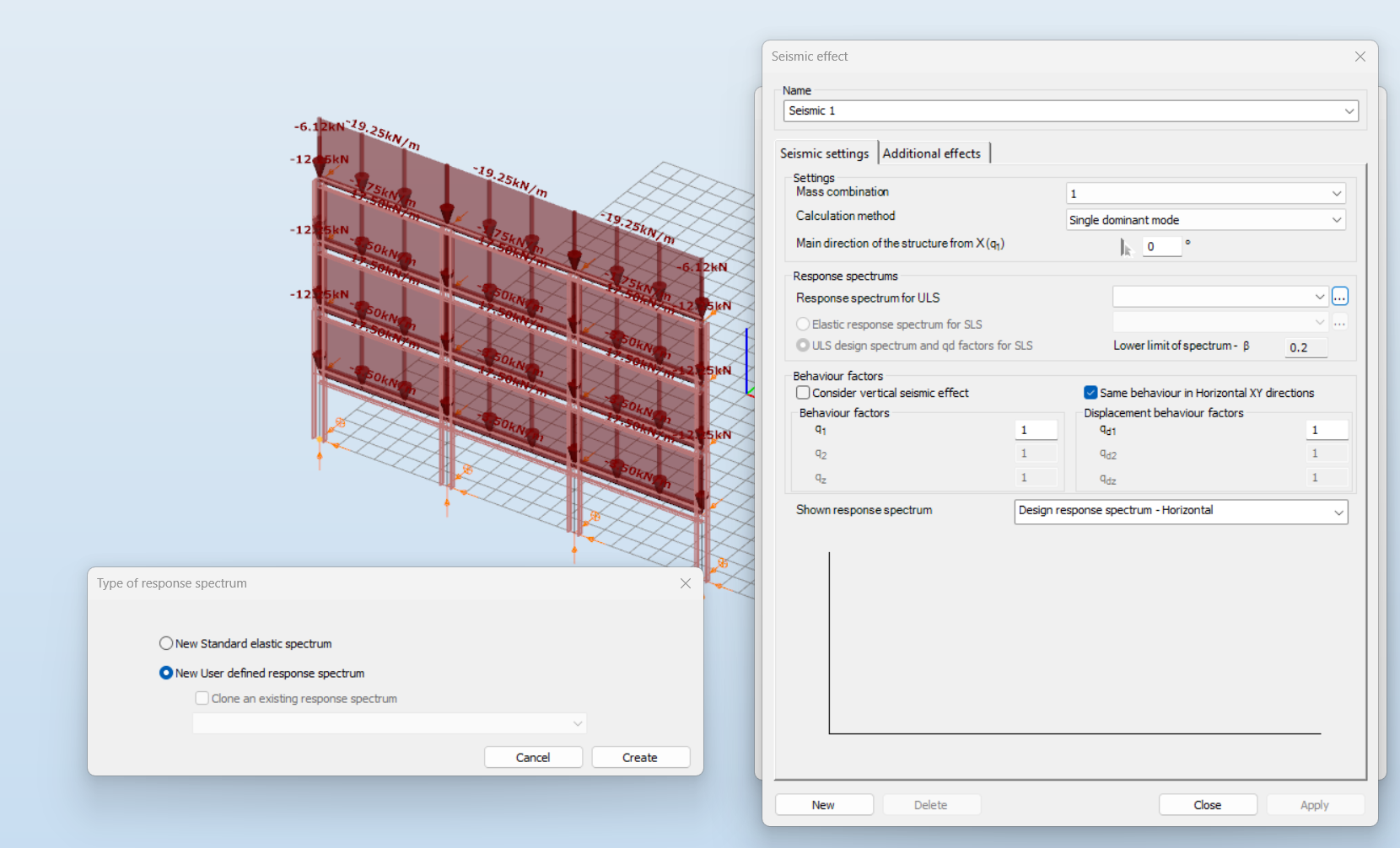

Introduction
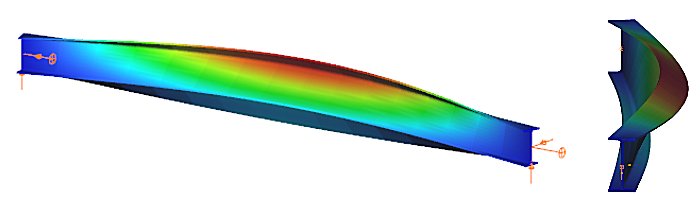
When a beam, bent in a plane, is allowed to move and twist freely between its two support points, in addition to bending, sudden perpendicular displacement and twisting may occur: causing the beam to deviate out of its original plane. This phenomenon is illustrated in Figure 1, showing a single supported beam with I-section bent around the strong axis. As the bending moment in the vertical plane increases, reaching a critical value, the beam undergoes abrupt lateral movement and twisting between the supports. This phenomenon is called lateral torsional buckling (LTB), which is a loss of stability mode that can apply to both perfect beams and real beams.
The design of the beam against LTB is fully analogous to the design of a compressed column against flexural buckling. The analogy is illustrated in Table 1, where the corresponding parameters are shown that affect the two buckling resistances:
| Flexural (column) buckling | Lateral torsional buckling |
|---|---|
| design force ($N_{Ed}$) | design moment ($M_{Ed}$) |
| critical force ($N_{cr}$) | critical moment ($M_{cr}$) |
| column slenderness ($\frac{}{\lambda}$) | beam slenderness ($\frac{}{\lambda}_{LT}$) |
| buckling reduction factor ($\chi$) | buckling reduction factor ($\chi_{LT}$) |
| buckling resistance ($N_{b,Rd}$) | buckling resistance ($M_{b,Rd}$) |
The critical moment of the perfect beam is determined at the location of the maximum value of the My,Ed design bending moment diagram. For a doubly symmetrical I cross-section:
$$M_{cr}=C_1\frac{\pi^2EI_z}{(k_z⋅L)^2}\left[\frac{I_\omega }{I_z}+ \frac{(k_zL)^2GI_t}{\pi^2EI_z}\right] ^{0.5} $$
where kz is the coefficient of restraint about the weak axis of the cross-section, G is the shear modulus, and It and Iω are the pure (St. Venant) and warping torsional moments of inertia of the cross-section. The value of the factor C1 depends on the shape of the bending moment diagram and its value can be found in appropriate tables and manuals. For a constant moment diagram, C1=1.0. The formula for the other design parameters, in particular the buckling reduction factor $\chi_{LT}$, depends on the design standard considered.
Lateral torsional buckling resistance by EN1993-1-1
The design of the beam against LTB (load capacity check) according to EC3-1-1 shall be carried out in the following steps:
gateDesigning a lattice girder
The design of the bars of a truss (lattice girder) structure does not require any special theoretical knowledge: normally, the truss bars are designed as compressed and/or tensioned bars, neglecting bending moments and shear forces. The dimensioning of compression bars is nowadays carried out using a model-based computer procedure. For details, see the knowledge base material Design of columns against buckling. Here, only the determination of the deflection length of the compressed bars is presented.
The most important parameter for the dimensioning of a compressed bar is the slenderness:
$$\overline{\lambda}=\sqrt\frac{Af_y}{N_{cr}}$$
where
$$N_{cr}=\frac{\pi^2El}{(kL)^2}$$
where the buckling length factor k is recommended by EN1993-1-1 to facilitate manual calculations:
| Type of the bar | Direction of buckling | k |
|---|---|---|
| chord | – in-plane – out-of-plane | 0.9 0.9 |
| bracing | – in-plane – out-of-plane | 0.9 1.0 |
Software using model-based computational methods (e.g. Consteel software) determines the elastic critical force Ncr directly by finite element numerical methods, taking into account the behaviour of the entire lattice girder, instead of the above conservative formula. The following example is intended to illustrate the relationship between the manual design procedure proposed by the standard and the results of the modern model-based numerical procedure.
- Let the structural model of the lattice girder under consideration be the Consteel model shown in Figure 1.
- Let the load shown correspond to the design load combination of the girder.
- Determine the deflection length of the most stressed compressed chord member using finite element numerical stability analysis.
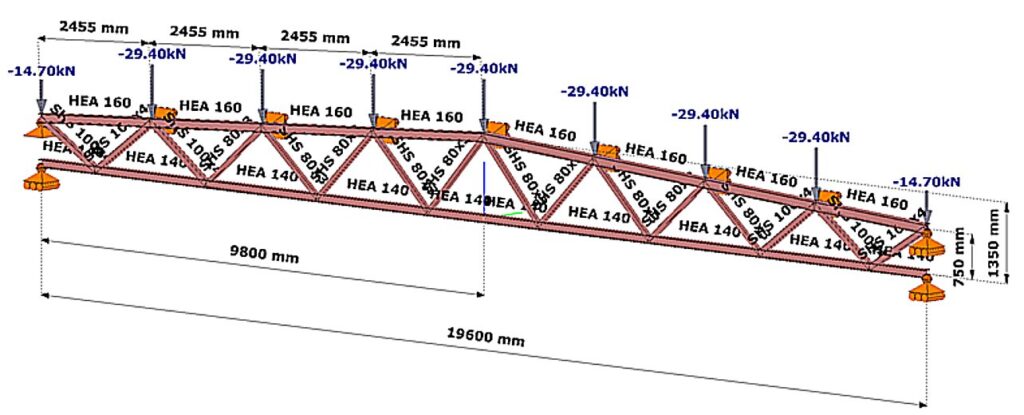
(Consteel software)
Relationship between procedures
The steps of the calculation are:
Buckling stability analysis
The stability analysis of the elastic model shows the governing buckling mode of the lattice structure and the corresponding elastic critical load factor αcr (Figure 2).
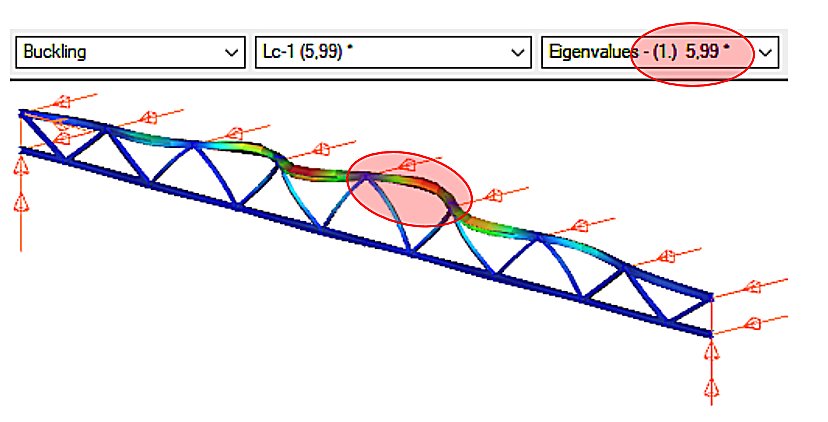
We can see that the upper chord of the perfectly elastic model is deflected laterally under load. The load that causes this elastic buckling is the critical load, whose value is given by the product of the design load and the critical load factor αcr=5.99.
gateThe evolution of compressed bar (column) design
One of the characteristic features of steel structures made of bars (e.g. lattice girders) is the compressed bar. We speak of a compressed bar when the structural element, which usually has a straight axis, is loaded by a compressive force P applied centrally (Figure 1).

Figure 2 illustrates the evolution of compressed bar (column) design. In the beginning (in the old days), master builders determined the load-bearing capacity of compressed columns of different materials and sizes on the basis of the experience accumulated over the centuries, passed down from master to apprentice. A significant change was brought about by the application of classical mathematical differential analysis to engineering. The Swiss mathematician and physicist Euler (1707-1783) solved the problem of the deflection of a compressed elastic line, which could be applied to the solution of the elastic compressed bar (Euler’s force). In the following centuries, engineers recognised that Euler’s force only gave an acceptable approximation to the real load capacity of a compressed bar in certain cases (mainly for large slender bars). Many solutions for the bearing capacity of a compressed bar were developed that were more advanced than the Euler formula, but it was not until the huge structural engineering boom following World War II that significant changes were made. Compression bar experiments were carried out in every major structural laboratory in the world, and a database of over two thousand experiments was compiled from the results. The load capacity of the pressure bar was given by a formula based on the database, using the method of mathematical statistics.
This methodology is still dominant today: ‘the dimensioning of the compressed bar has become a political issue for the steel construction profession…’. Understanding the principle of compressed bar design is therefore essential for the structural engineer.
The right side of the Figure 2 also contains a hint for the future. At the level of scientific research, it is already present that the load capacity of a real compressed column can be determined by mathematical-mechanical simulation. Indeed, in the near future, databases that go beyond anything we know today can be created using supercomputers. On the basis of such a gigantic database, artificial intelligence could, at least in principle, supersede existing engineering knowledge and methodology. But the reality is that structural engineering is not one of the pull sectors (such as the defense or automotive industries), so this new shift in design theory is certainly a long way off.
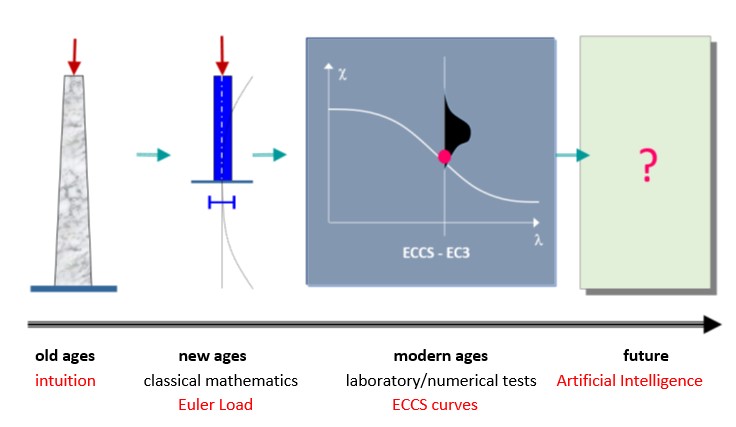
In the following, the Euler force and the experimentally based standard design formula, which are of major importance to structural steel engineering today, are discussed in detail.
Buckling strength of the ideal columns: the Euler force
Assume that the hinged compressed column shown in the Figure 3 has the following properties:
- perfectly straight,
- its material is perfectly linearly elastic,
- centrally compressed.
Under the above conditions, perform the compressed column experiment using Consteel software: run the Linear Buckling Analysis (LBA) calculation. The result is illustrated in Figure 3.
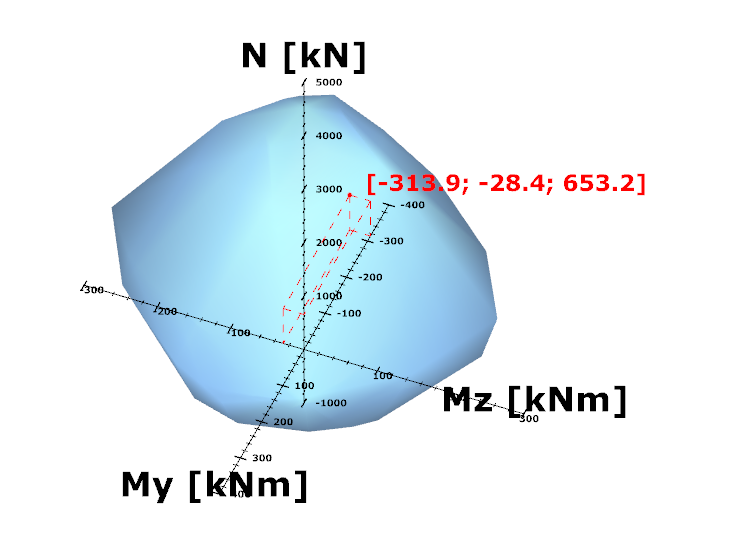
gateIn Consteel, the calculation of cross sectional interaction resistance for Class 3 and 4 sections is executed with the modified Formula 6.2 of EN 1993-1-1 with the consideration of warping and altering signs of component resistances. Let’s see how…
Application of EN 1993-1-1 formula 6.2
For calculation of the resistance of a cross section subjected to combination of internal forces and bending moments, EN 1993-1-1 allows the usage -as a conservative approximation- a linear summation of the utilization ratios for each stress resultant, specified in formula 6.2.
$$\frac{N_{Ed}}{N_{Rd}}+\frac{M_{y,Ed}}{M_{y,Rd}}+\frac{M_{z,Ed}}{M_{z,Rd}}\leq 1$$
As Consteel uses the 7DOF finite element and so it is capable of calulcating bimoment, an extended form of the formula is used for interaction resistance calculation to consider the additional effect.
$$\frac{N_{Ed}}{N_{Rd}}+\frac{M_{y,Ed}}{M_{y,Rd}}+\frac{M_{z,Ed}}{M_{z,Rd}}+\frac{B_{Ed}}{B_{Rd}}\leq 1$$
Formula 6.2 ignores the fact that not every component results the highest stress at the same critical point of the cross-section.
In order to moderate this conservatism of the formula, Consteel applies a modified method for class 3 and 4 sections. Instead of calculating the maximal ratio for every force component using the minimal section moduli (W), Consteel finds the most critical point of the cross-section first (based on the sum of different normal stress components) and calculates the component ratios using the W values determined for this critical point. Summation is done with considering the sign of the stresses caused by the components corresponding to the sign of the dominant stress in the critical point.
(For class 1 and 2 sections, the complex plastic stress distribution cannot be determined by the software. The Formula 6.2 is used with the extension of bimoments to calculate interaction resistance, but no modification with altering signs is applied)
Example
Let’s see an example for better explanation.
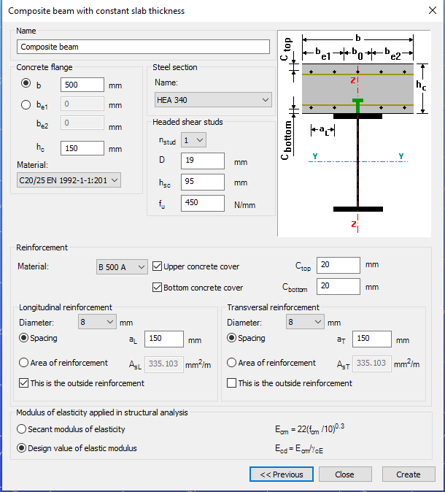
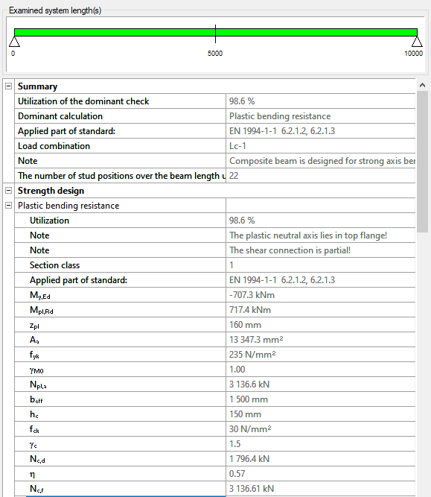
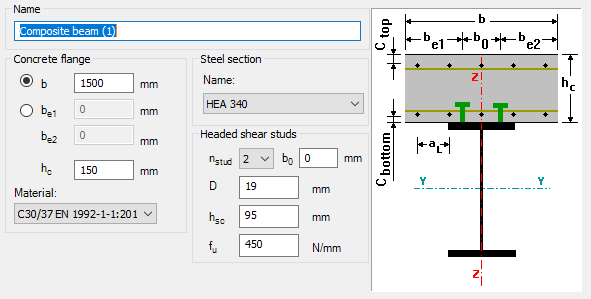
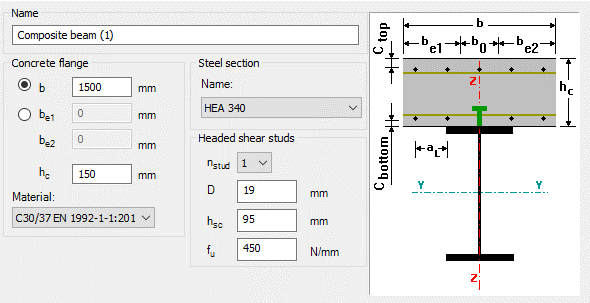
GATEDid you know that you could use Consteel to determine the optimum number of shear connectors for composite beams?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free

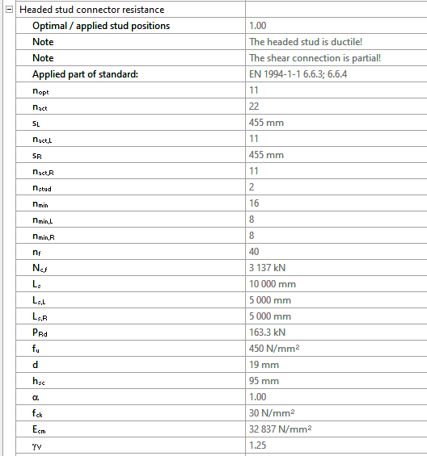
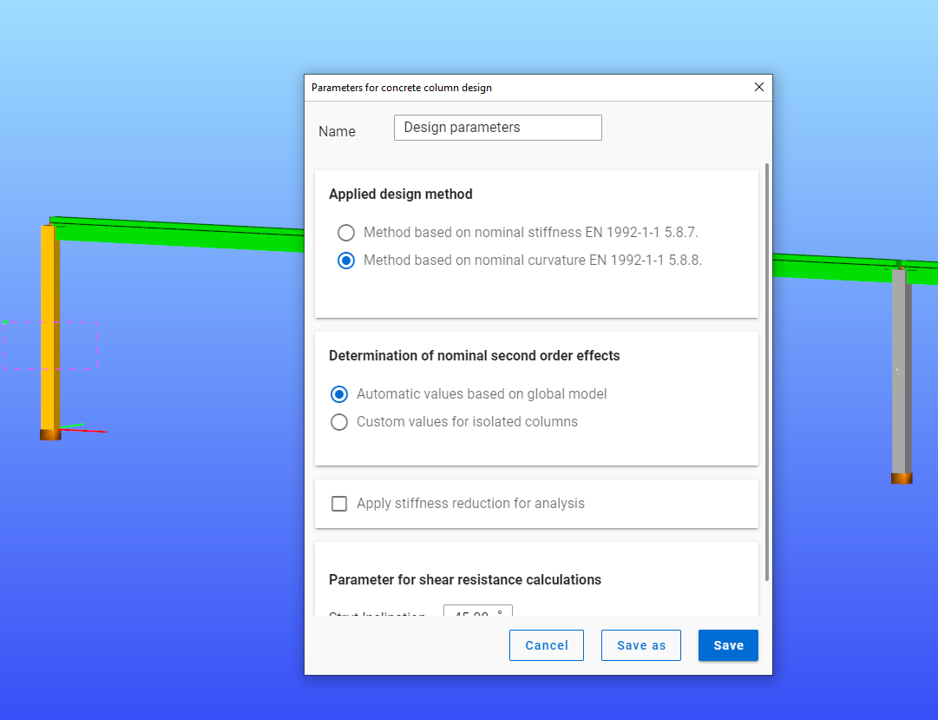
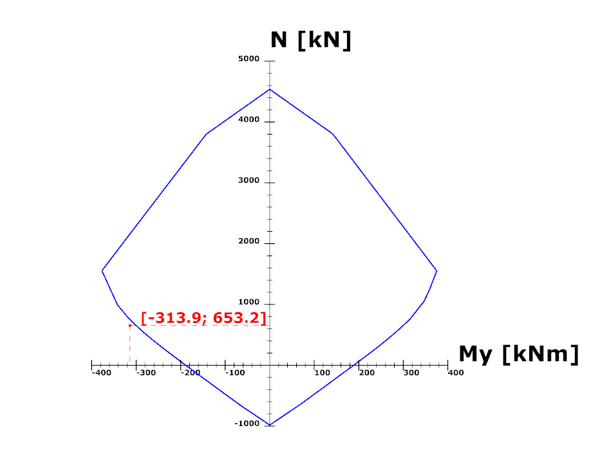
Did you know that you could use Consteel to determine automatically the second order moment effects for slender reinforced concrete columns?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free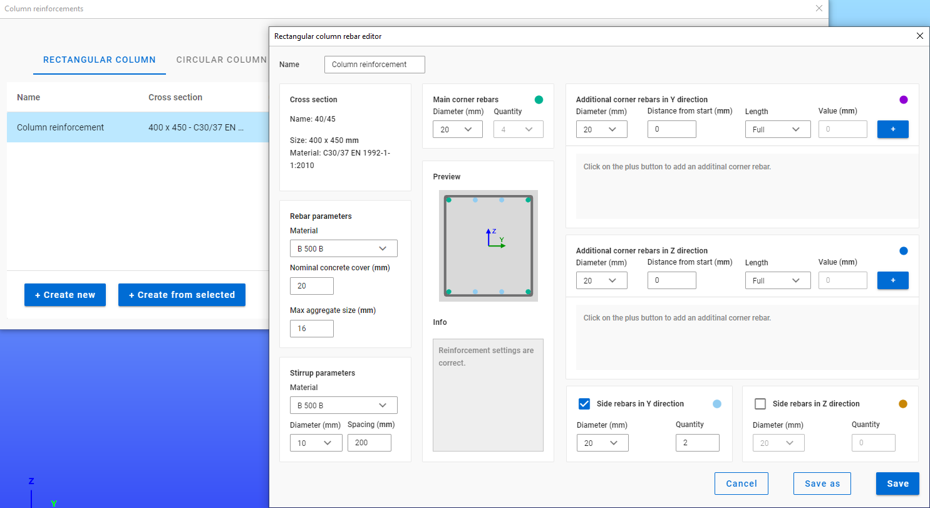
Did you know that you could use Consteel to perform local and distortional buckling checks for cold-formed members?
First, sections must be loaded into the model. To load cold-formed sections, you can choose from four options: From library, Macro section, Draw section, or My library.
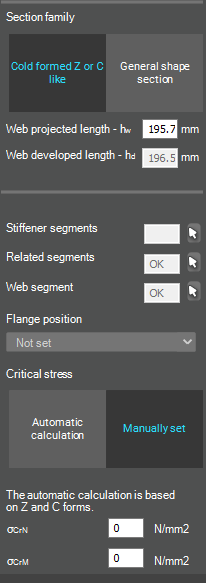
After the first-order and buckling analyses are completed, you can proceed to the Ultimate limit state check settings and enable the steel design cross-section and buckling checks. At the bottom of the steel design section, there is an option to Consider the supplementary rules from EN 1993-1-3 for the design of cold-formed sections. This checkbox must be selected if you want to design cold-formed sections.
When the calculation is finished, by opening the Section module, we can review all the properties of the Effective section of the elastic plate segment model. By opening each plate element, we can verify the length, effective length, thickness, effective thickness, slenderness, and reduction factor separately. In addition, the properties of the stiffeners can also be verified: area, moment of inertia, lateral spring stiffness, critical stress, reduction factor, compressive stress, reduced effective area, and reduced thickness.
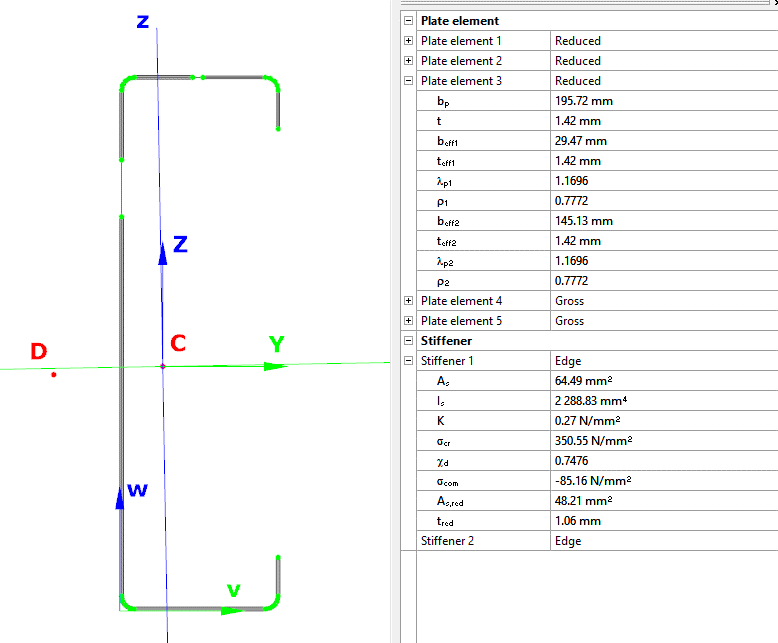
Similarly, the stresses can also be checked from the Properties tab. In the colored figure or diagram view, all the calculated stresses can be seen together with their resultants.
Consteel automatically takes into account the effect of distortional buckling when calculating the effective sections of cold-formed thin-walled sections.
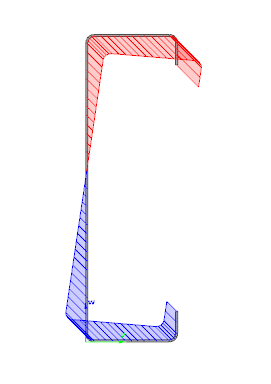
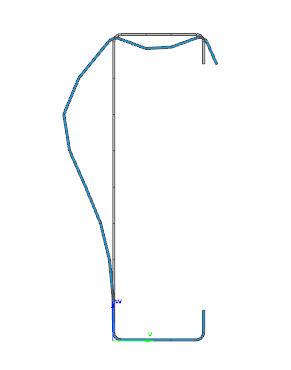
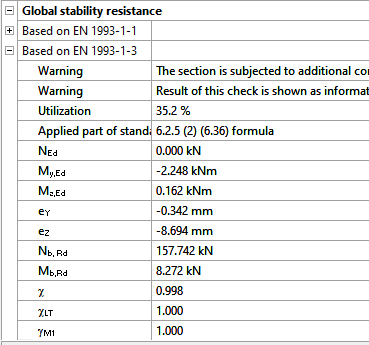
Moving on to the Standard resistance tab in the Section module, all calculated results can be verified, not only the dominant one. By opening the Global stability resistance check, we can see that, since we enabled the option to consider the supplementary rules from EN 1993-1-3 for the design of cold-formed sections, results are available both according to EN 1993-1-1 and according to EN 1993-1-3.
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free