Diskrete Wölbsteifen

Theoretischer Hintergrund

In der Balkentheorie hat die Torsion zwei Komponenten.

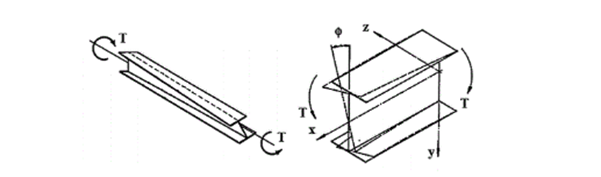
Saint-Venant'sche Torsion

Die meisten geschlossenen dünnwandigen Hohlprofile tragen Querschnittsrotationen mittels der St. Venant′schen Torsion ab, bei der nur Schubspannungen τ_t (oder τ_p) auftreten.

Verwölbung

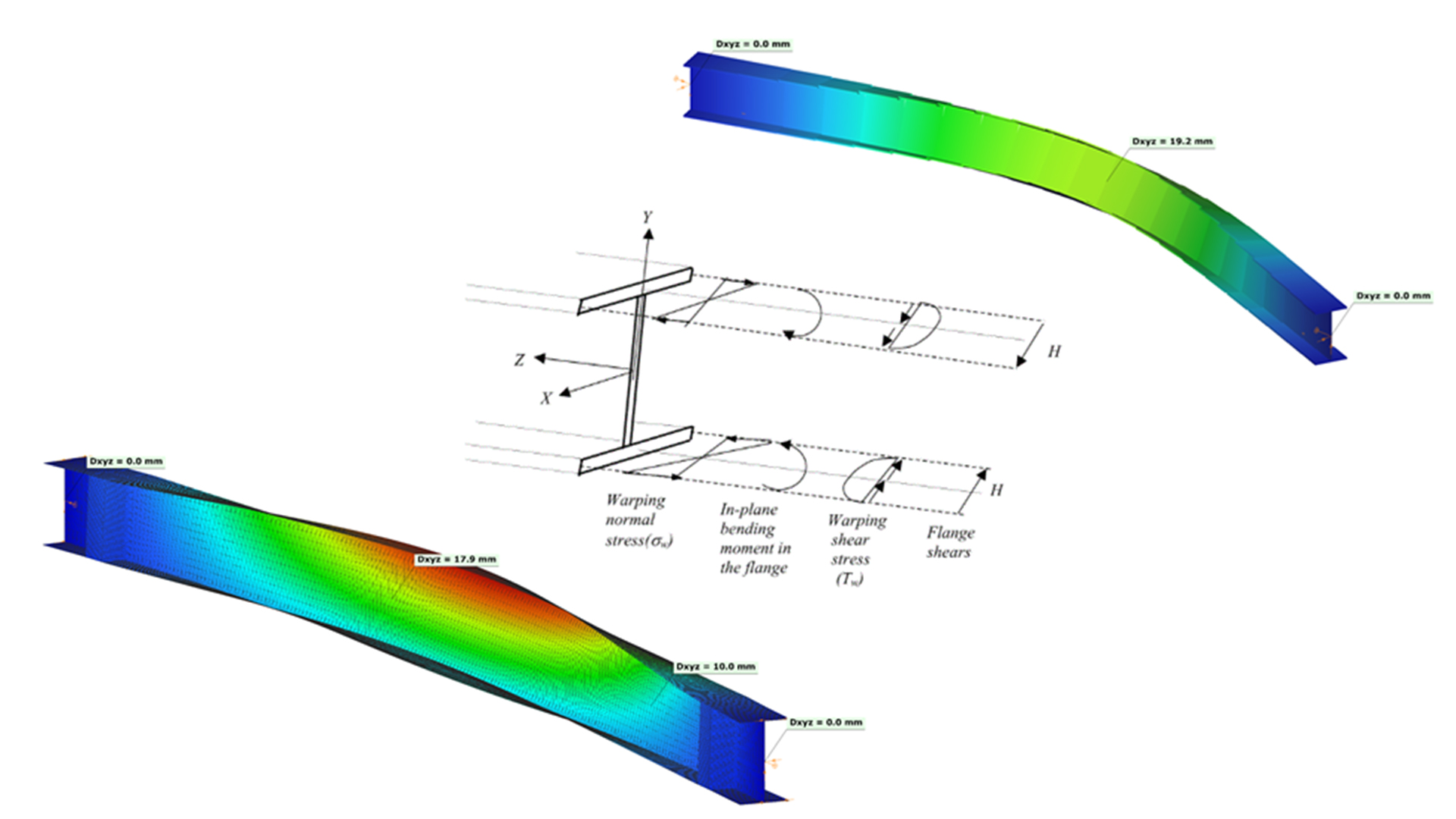
Bei dünnwandigen offenen Querschnitten tritt als weiterer und viel wichtigerer Torsionswiderstand noch die Querschnittsverwölbung hinzu, bei der zusätzlich Normalspannungen (und baupraktisch vernachlässigbare sekundäre Schubspannungen) auftreten [1].

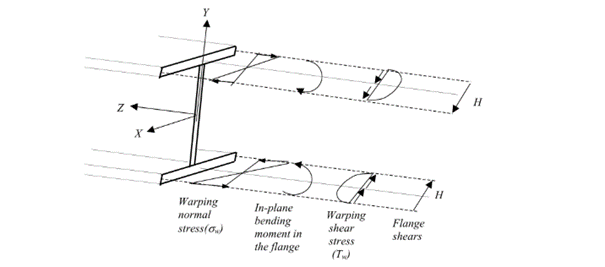
Die Verwölbung erzeugt bei I-artigen Querschnitten in den Flanschen gegenläufige lokale Querbiegemomente (In-plane bending moments). Daraus resultieren erhebliche Normalspannungen und geringfügige Schubspannungen (Bild 2).

Torsionsbeanspruchte Träger mit dünnwandigen offenen Querschnitten allein nur mit der St. Venant′schen Torsion zu berechnen führt meistens zu vollkommen falschen und auch unwirtschaftlichen Ergebnissen bei den Verformungen und Tragfähigkeitsnachweisen. Daher sollte immer die Wölbkrafttorsion angewendet werden, weil nur dann das Torsionsverhalten korrekt und wirtschaftlich erfasst wird.
Bei Doppelbiegung und Biegedrillknicknachweisen ist grundsätzlich die Biegewölbkrafttorsion 2. Ordnung zu verwenden!

Diskrete Wölbbehinderungen

Die Tragfähigkeit von Trägern mit dünnwandigen offenen Profilen bei Torsionsbeanspruchung und Biegedrillknicken kann durch eine Verbesserung der Wölbsteifigkeit erhöht werden. Dazu können zusätzliche Querschnittsversteifungen an geeigneten Stellen des Trägers angeordnet werden, die die gegenseitige Querverschiebung der Trägerflansche wegen der Torsionssteifigkeit der Steifen behindert. In ConSteel können derartige Steifen bei dem Superbalken mittels spezieller Steifen-Tools angeordnet werden. ConSteel erzeugt dann automatisch eine (elastische) Wölblagerung an der Steifenposition, wobei die Steifigkeit der Wölbsteife analytisch berechnet wird (s. u.). Die Steifigkeit kann aber auch manuell mit einem Eingabewert spezifiziert werden (z. B. nach [3]).

Die folgenden Steifentypen stehen zur Verfügung:

• Flachsteifen
• T - Steifen
• L - Steifen
• Hohlsteifen

Die allgemeine Formel der Wölbsteifigkeit lautet:

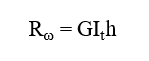
mit

R_ω: diskrete Wölbfedersteifigkeit

G: Schubmodel

GI_t: Saint-Venant'sche Torsiossteifigkeit

h: Steifenhöhe

Wölbsteifigkeit verschiedener Steifentypen

Flachsteife am Steg:

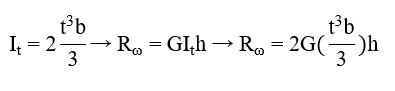
mit

b: Steifenbreite [mm]

t : Steifendicke [mm]

h: Steifenhöhe [mm]

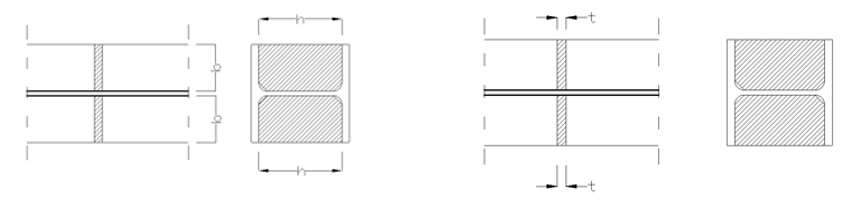
T - Steife:

mit

b₁: Bindeblechbreite [mm]

t₁: Bindeblechdicke [mm]

b₂: Stegsteifenbreite [mm]

t₂: Stegsteifendicke [mm]

h: Stegsteifenhöhe [mm]

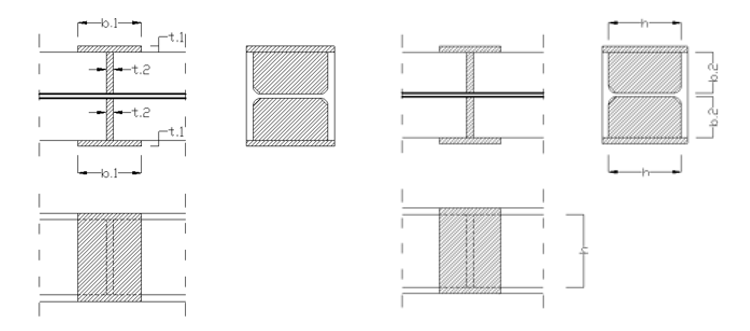
L-Steife:

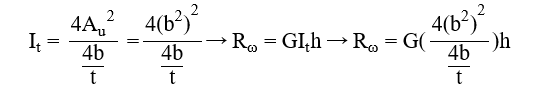
mit

b: Schenkellänge L-Profil [mm]

t: Dicke L-Profil [mm]

h: Höhe L-Profil (= Steghöhe I - Profil) [mm]

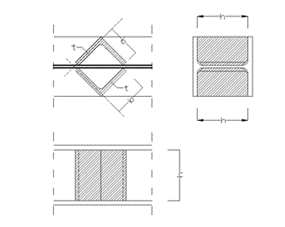
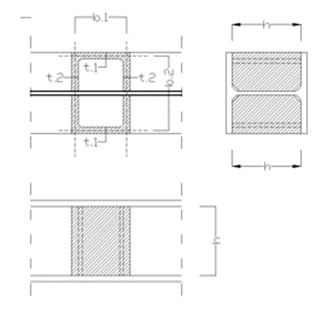
Hohlsteife (doppelte U-Steife):

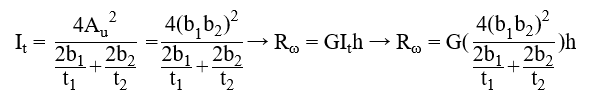
mit

b₁: Breite des Hohlsteifenstegs [mm]

t₁: Dicke des Hohlsteifenstegs [mm]

b₂: Breite des Hohlsteifenflansches [mm]

t₂: Dicke des Hohlsteifenflansches [mm]

h: Höhe der Steife (= Steghöhe I - Profil) [mm]

Zahlenbeispiel

Das folgende Beispiel zeigt den versteifenden Einfluss auf den maßgebenden Eigenwert und die Tragfähigkeit gegen Biegedrillknicken je einer Hohlsteife kurz vor den beidseitigen Gabellagerungen. In Bild 11 mit der Schalenelementierung ist der versteifende Effekt (keine Verwölbung am Trägerende) deutlich zu erkennen.

Schalenmodell

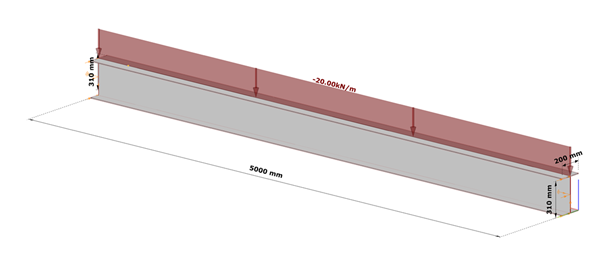
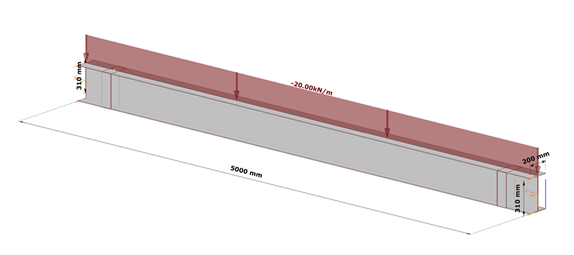
Bild 7 zeigt den beidseitig starr gabelgelagerten Einfeldträger mit Schalenelementierung und einer Gleichstreckenlast am Obergurt.

Die Tabellen 1 und 2 enthalten die Geometrie- und Materialdaten des Schweißquerschnittes. Die Balkenlänge beträgt 5000 mm und die Lastexzentrizität ist 150 mm in z-Richtung.

Name	Dimension	Wert
Breite der Flansche	[mm]	200
Dicke der Flansche	[mm]	10
Steghöhe	[mm]	300
Stegdicke	[mm]	10

Name	Dimension	Wert
E-Modul	[N/mm2]	210000
Querkontraktion	[-]	0,3
Yield strength	[N/mm2]	300

Hohlsteife

Die beiden Hohlsteifen (Tabelle 3) werden in der Nähe der Stabenden platziert (Bild 8).

Name	Dimension	Wert
Breite der Hohlsteife	[mm]	100
Breite der Bindebleche	[mm]	100
Gesamtbreite der Hohlsteife	[mm]	200
Höhe der Hohlsteife	[mm]	300
Blechdicke der Hohlsteife	[mm]	10

Balkenmodell mit 7 Verformungsfreiheitsgraden

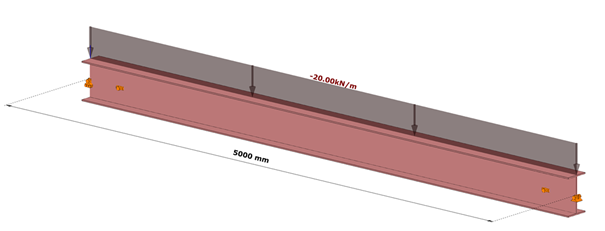
Bei dem Balkenmodell mit 7 Verformungsfreiheitsgraden kann der gleiche Versteifungseffekt mit lokalen Wölbfedern an den Stellen der Hohlsteifen erreicht werden (Bild 9).

Manuelle Berechnung der Wölbsteifigkeit

Die Berechnung erfolgt mit den Formeln des vorangegangenen Kapitels [2.1.4]:

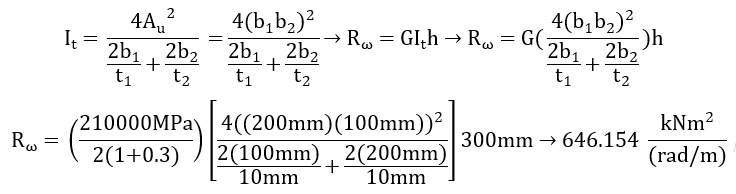
ConSteel Berechnungsergebnisse

Die jeweils zum niedrigsten Eigenwert gehörenden Eigenformen des Biegedrillknickens sind in den Bildern 10 und 11 dargestellt. Tabelle 4 enthält die zu 20 kN/m gehörenden kritischen Lastfaktoren der Balken-- und Schalenelementierung mit und ohne Hohlsteifen. Die Ergebnisse zeigen eine gute Übereinstimmung.
Das nach DIN EN 1993-1-1 berechnete Traglastmoment des Trägers mit Balkenelementierung mit und ohne Hohlsteifen ist Tabelle 5 zu entnehmen. Die Traglasterhöhung beträgt hier nennenswerte 45 %.

Erste Eigenform mit Balkenelementierung

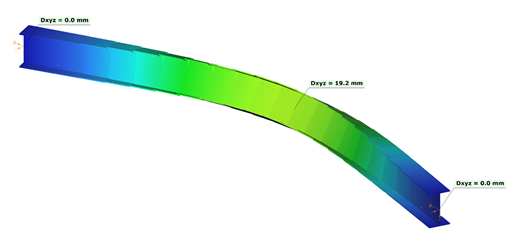
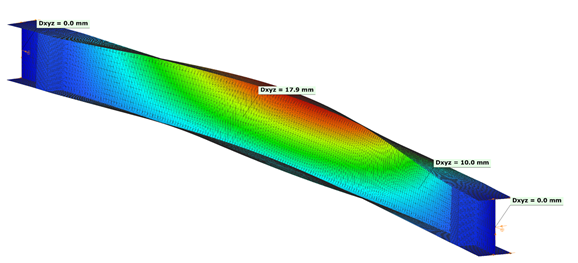
Erste Eigenform mit Schalenelementierung

Ergebnis	Modell	Dimension	Wert
Eigenwert	Balkenelementierung	[-]	6.85
Eigenwert	Schalenelementierung	[-]	6.76

Ergebnis	Model	Dimension	Value [kNm]
Traglastmoment Mb,Rd	Orginaler Balken	[kNm]	101.07
Traglastmoment Mb,Rd	wölbversteifter Balken	[kNm]	146.15

Literatur

[1] Webseite: https://structural-analyser.com/domains/SteelDesign/Torsion/

[2] Webseite: http://www.isa.fh-trier.de/home/Projekte/Nagolnij/index_63.html

[3] Univ.-Prof. em. Dr.-Ing. Rolf Kindmann, Stahlbau, Teil 2: Stabilität und Theorie II. Ordnung, April 2008

[4] Pascal Händler, The Bearing Behaviour of Warping Springs in Torsionally Loaded I–Beams, April 2016;
https://www.researchgate.net/publication/327511352_The_Bearing_Behaviour_of_Warping_Springs_in_Torsionally_Loaded_I-Beams