This study explores how Computational Fluid Dynamics (CFD)–based pressure simulation results can be compared and aligned with wind tunnel experiments and standardized design methods, reflecting the practical process engineers follow when assessing wind loads. The aim is to provide a framework for interpreting and applying simulation outputs with more confidence, supported by a clear workflow. To ensure that the findings are robust and generalizable, the analysis is grounded in a comprehensive parametric dataset: the Tokyo Polytechnic University (TPU) database of isolated low-rise buildings without eaves. This resource contains detailed pressure coefficient data for 116 building models—featuring flat, gable, and hip roofs—tested under eight wind directions, yielding more than 800 individual cases for comparison. To align these wind tunnel tests with the standard procedures the main orthogonal directions were investigated.
Compliance with standards
Before validating CFD results against established references, it is important to set the Eurocode baseline for wind load evaluation. From the wind effect side, a previous article covers how the specific wind profiles are determined and harmonized with the simulations during the preprocess phase, while for wind actions the Eurocode defines two main approaches:
- Wind pressure on surfaces – expressed through pressure coefficients for a range of building geometries.
- Wind forces on special structures – i.e. lattice towers.
Since CFD inherently produces surface pressure distributions, this study focuses exclusively on the first approach—wind pressure on surfaces—applied to closed buildings. For the purposes of this comparison, only vertical walls and simple roof types (flat and duopitched) were considered.
Under Eurocode procedures, building surfaces are subdivided into zones whose dimensions are determined by the building’s proportions. In practice, the characteristic zoning length, e , defines the extent of the regions for which local pressure coefficients are specified.
Therefore, to ensure a coherent comparison between wind tunnel tests and simulation results, the mesh refinement must be adjusted accordingly, for each previously presented geometrical case of the dataset for both principal orthogonal directions, which in turn makes a parametric study indispensable.
Parametric methodology
To support the parametric study, a dedicated script was developed to generate results for all three scenarios simultaneously: wind tunnel tests, simulation outputs, and standard-based approaches.
gateBevezetés
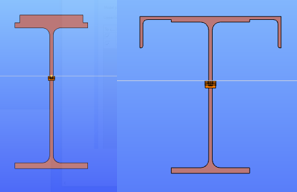
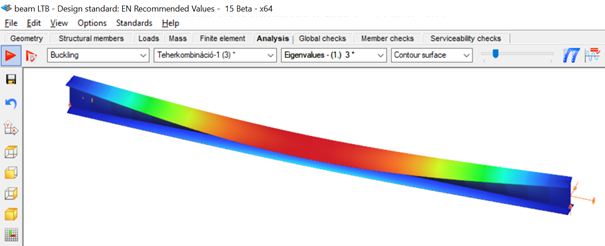
Amennyiben a síkban hajlított gerenda szabadon elmozdulhat és elcsavarodhat a két támaszpontja között, akkor a lehajlás mellett hirtelen merőleges elmozdulás és elcsavarodás jöhet létre: a gerenda kifordul a síkjából. Ezt a jelenséget szemlélteti az 1. ábra, amely egy kéttámaszú, az erős tengely körül hajlított I keresztmetszetű gerendát mutat: a függőleges síkban történő hajlítás során, amikor a nyomaték elér egy kritikus értéket, a gerenda hirtelen oldalirányban elmozdul és elfordul a két támasz között. Ez a jelenség a kifordulás, amely stabilitásvesztési mód a tökéletes gerendára és a valódi gerendára egyaránt vonatkozhat.
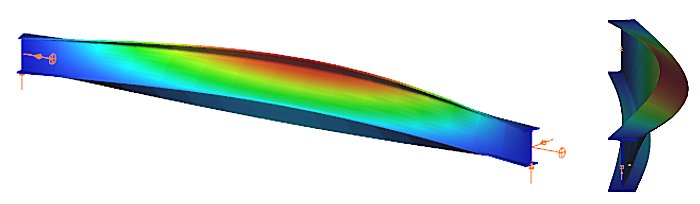
A gerenda kifordulással szembeni méretezése teljes mértékben analóg a nyomott oszlop kihajlási elleni méretezésével. Az analógiát az 1. táblázat szemlélteti, ahol feltüntettük a kihajlási és a kifordulási ellenállást befolyásoló, egymásnak megfelelő paramétereket.
| Kihajlás | Kifordulás |
|---|---|
| tervezési nyomóerő ($N_{Ed}$) | tervezési nyomaték ($M_{Ed}$) |
| kritikus erő ($N_{cr}$) | kritikus nyomaték ($M_{cr}$) |
| kihajlási karcsúság ($\frac{}{\lambda}$) | kifordulási karcsúság ($\frac{}{\lambda}_{LT}$) |
| kihajlási csökkentő tényező ($\chi$) | kifordulási csökkentő tényező ($\chi_{LT}$) |
| kihajlási ellenállás ($N_{b,Rd}$) | kifordulási ellenállás ($M_{b,Rd}$) |
A tökéletes gerenda kritikus nyomatékát a My,Edtervezési hajlítónyomaték-diagram maximális értékének helyén kell meghatározni. Kétszeresen szimmetrikus I keresztmetszet esetén:
$$M_{cr}=C_1\frac{\pi^2EI_z}{(k_z⋅L)^2}\left[\frac{I_\omega }{I_z}+ \frac{(k_zL)^2GI_t}{\pi^2EI_z}\right] ^{0.5} $$
ahol kz a keresztmetszet gyenge tengelye körüli befogási tényező, G a nyírási modulus, It és Iω pedig a keresztmetszet tiszta (St. Venant) és gátolt csavarási tehetetlenségi nyomatéka. A C1 tényező értéke a hajlító nyomatéki diagram alakjától függ, az értéke megfelelő táblázatokban és kézikönyvekben megtalálható. Konstans nyomatéki ábra esetén C1=1.0. A többi tervezési paraméter, különösen a $\chi_{LT}$ kifordulási csökkentő tényező képlete a figyelembe vett tervezési szabványtól függ.
Kifordulási ellenállás az EN1993-1-1 szerint
A hajlított gerenda kifordulás elleni méretezését (teherbírás-ellenőrzést) az EC3-1-1 szerint a következő lépésekben kell elvégezni:
gateRácsos tartó szerkezet méretezése
A rácsos tartók globális (rúdszerkezeti szintű) méretezése nem igényel különleges elméleti ismeretet: rendszerint a hajlítónyomatékok és a nyíróerők elhanyagolásával a rácsos tartók rudjait nyomott és/vagy húzott rúdként méretezzük. A nyomott rudak méretezését manapság modell alapú számítógépes eljárással hajtjuk végre. Ennek részleteit lásd a Nyomott rúd méretezése kihajlás ellen című tudásbázis anyagban. Itt csak a nyomott rudak kihajlási hosszának meghatározását mutatjuk be.
A nyomott rúd méretezésénél a legfontosabb paraméter a rúdkarcsúság:
$$\overline{\lambda}=\sqrt\frac{Af_y}{N_{cr}}$$
ahol
$$N_{cr}=\frac{\pi^2El}{(kL)^2}$$
ahol a k kihajlási hosszt (befogási tényezőt) az EN1993-1-1 szabvány, a kézi számítások megkönnyítése érdekében, az alábbiak szerint javasolja felvenni:
| Nyomott rúd típusa | Kihajlás iránya | k |
|---|---|---|
| övrúd | – tartó síkjában – tartó síkjára merőlegesen | 0.9 0.9 |
| rácsrúd | – tartó síkjában – tartó síkjára merőlegesen | 0.9 1.0 |
A modell alapú számítógépes eljárásokon alapuló szoftverek (pl. a Consteel szoftver) a fenti konzervatív szabály helyett az Ncr rugalmas kritikus erőt közvetlenül végeselemes numerikus módszerrel, a teljes rácsos tartó viselkedésének figyelembe vételével, határozzák meg. Az alábbi példával a szabvány által javasolt kézi méretezési eljárás és a modern, modell alapú numerikus eljárás eredményének viszonyát kívánjuk szemléltetni.
- Legyen a vizsgált rácsos tartó szerkezeti modellje az 1. ábrán látható Consteel modell.
- A feltűntetett teher feleljen meg a tartó mértékadó tervezési teherkombinációjának.
- Határozzuk meg a legjobban igénybe vett nyomott övrúd kihajlási hosszát végeselemes numerikus stabilitási analízis segítségével.
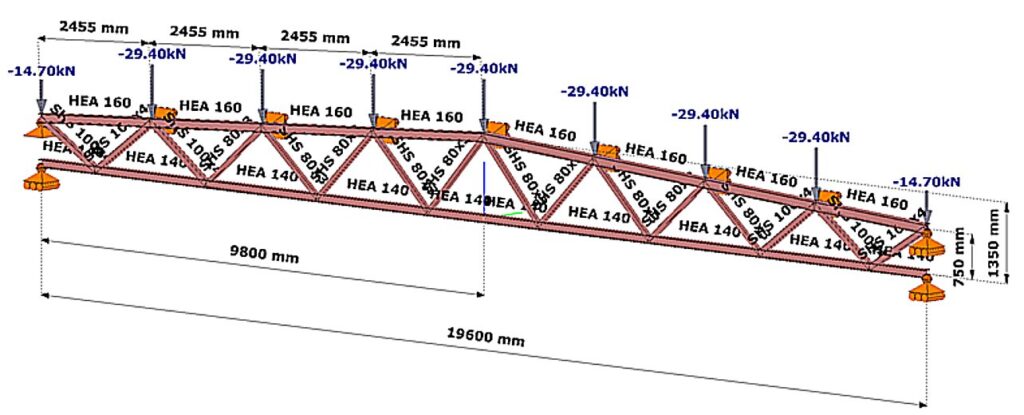
(Consteel szoftver)
Eljárások összehasonlítása
A számítás lépései a következők:
Rugalmas stabilitási analízis
A rugalmas modell stabilitási analízise megmutatja, hogy a rácsos szerkezet mértékadó stabilitásvesztési módját és az ahhoz tartozó αcr rugalmas kritikus teherszorzót (2. ábra).
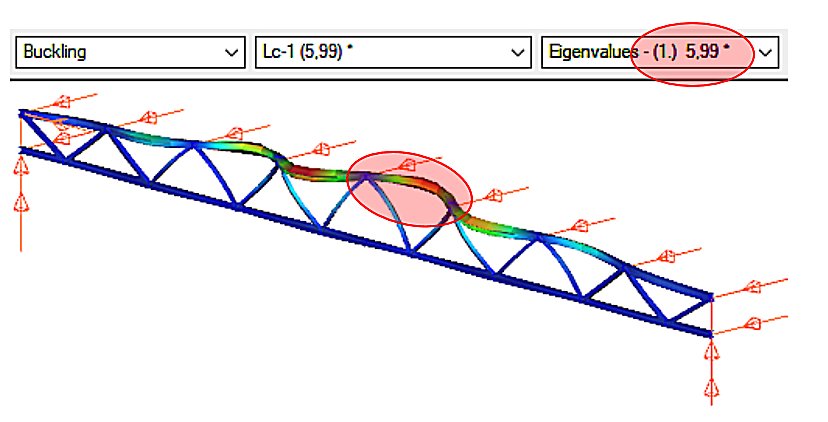
Láthatjuk, hogy a terhelés hatására a tökéletesen rugalmas modell felső öve oldalsó irányban kihajlást szenved. A teher, amely hatására a rugalmas kihajlás bekövetkezik, a kritikus teher, amelynek értékét a tervezési teher és az αcr=5.99 kritikus teherszorzó szorzata adja meg.
gateEz a rövid áttekintés mélyebben ás a Consteel megoldásába, egy alternatív szemléletet nyújtva az effektív keresztmetszeti tulajdonságok kiszámításához, és formálva a hagyományos megközelítéseket a szerkezeti elemzés és tervezés területén.
Határozzuk meg a 384-4 gerinclemezű és 300-8 övlemezű kétszersen szimmetrikus hegesztett I keresztmetszet szilárdsági kihasználtságát, amennyiben a keresztmetszet igénybevételei az NEd=500kN nyomóerő és az My,Ed=100kNm hajlító nyomaték. A keresztmetszet anyaga S235 minőségű.
Keresztmetszeti jellemzők számítása
Először vegyük fel a keresztmetszet adatait (szimmetrikus hegesztett I szelvény), amely alapján a Consteel software generálja az EPS (és GSS) (Online Kézikönyv/10.1.1 EPS (vékonyfalú szelvény) modell) keresztmetszeti modellt (1. ábra):
Amennyiben a keresztmetszet 4. osztályba tartozik, az effektív keresztmetszeti modellt a feltételezett normálfeszültségi eloszlás határozza meg. Az EC3-1-1 szerint a 4. keresztmetszeti osztályú szelvény EPS keresztmetszeti modellje kétféleképpen határozható meg:
- A módszer: tiszta igénybevételi állapotok alapján,
- B módszer: összetett igénybevételi állapot alapján.
Először az A módszerrel számoljuk ki a keresztmetszeti tulajdonságokat, majd a B módszerrel.
Keresztmetszeti jellemzők az A módszer alapján
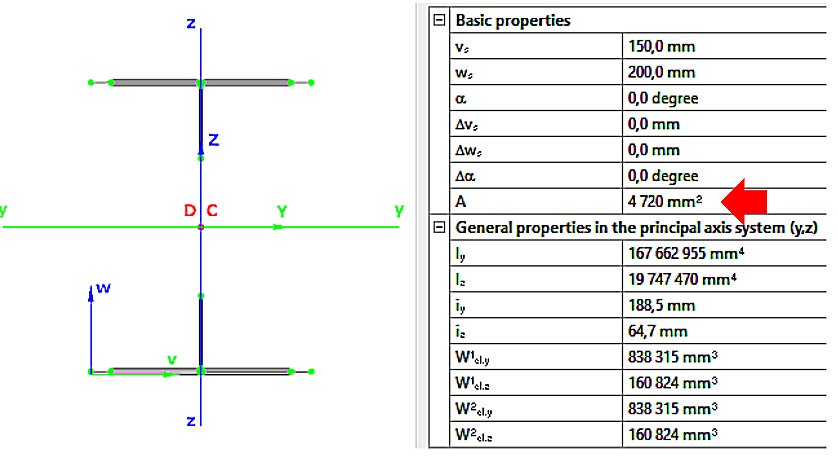
- NEd nyomóerő esetén (2. ábra):
- Aeff=4720mm2
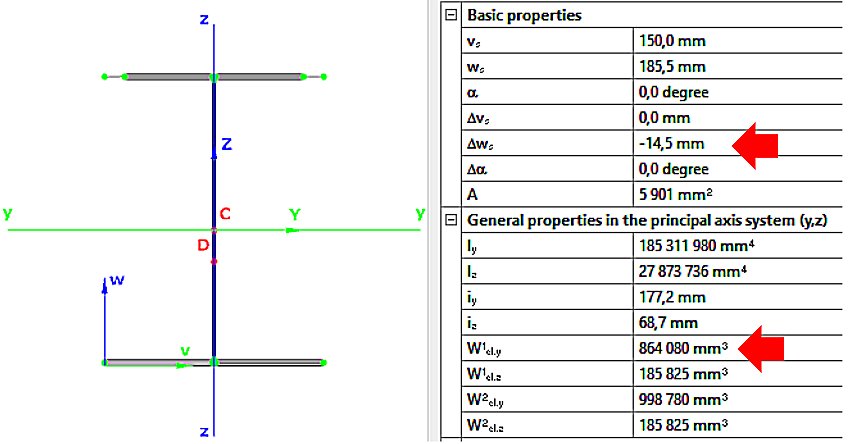
- My,Ed hajlító nyomaték esetén (3. ábra):
Weff,y,min=864080mm3
ez=14.5mm
Keresztmetszeti jellemzők a B módszer alapján
GATEIntroduction
During the lifetime of a steel structure changes often happen. These changes usually result an increase of loads acting on some of its elements which therefore may need to be strengthened.
Strengthening is usually done by welding additional steel plates to the existing members. In the case of I sections, usually, the flanges are reinforced to increase the bending moment capacity or the web is stiffened to avoid local buckling or crippling at support regions.
This paper will focus on the increase of bending moment capacity.
Lateral-torsional buckling resistance
The usual practice is to either increase the compression flange thickness by adding additional plates to it, or by widening it with the help of angles, as can be seen in the pictures below.
Although these can be very efficient ways to increase the bending moment capacity of a beam, welding on site is a complex process and might require the temporary removal of structural or non-structural elements connected to the flange of the beam. Welding especially “above the head” is difficult, the quality of weld seam needs to be properly checked.
Bending moment capacity of a beam might be limited by lateral-torsional buckling. If the section is not sufficiently restrained laterally against torsion, its actual load-bearing capacity will be lower than the value which depends purely on its section resistance.
In such cases, if the LTB behaviour could be directly improved, there would be no need to strengthen its cross-section along its full length. Here comes the Superbeam as a possible help.
Additional lateral restraining elements are often difficult to be added, therefore this is often not an option.
If we look at what LTB resistance of an I section depends on, we can see, that if we don’t want to change its cross section along its full length, it depends on the value of the reduction factor responsible to consider lateral-torsional buckling χLT.
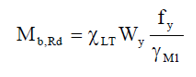
This reduction factor is calculated from the slenderness value of the beam, which needs to be improved (reduced) to result a lower, more favourable reduction factor.
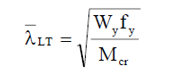
Without changing the cross section, the only way to do this is by improving the critical moment value. Increasing this value can be made not only by changing the cross-section but also by changing the boundary conditions.
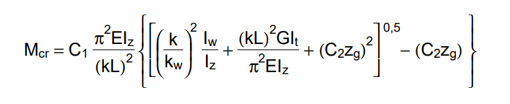
The value of parameters ‘k’ and ‘kw’ depend on the boundary conditions, where ‘k’ means a factor which depends on how the section is fixed against weak axis bending at its ends and ‘kw’ means a factor which depends on how the section is fixed against warping. Warping is the phenomenon when the upper and lower flange of an I section twist in opposite directions.
To change the end conditions is typically difficult, but a certain limitation of the twist of flanges relative to each other ie. preventing or limiting warping might be possible. Limitation of this twist can be obtained by connecting the flanges by an additional element which has non-zero torsional stiffness. This torsional stiffness will prevent the counter-rotation of the flanges and therefore the warping and allowing to consider a ‘kw’ value different than 1.0 in this formula.
Consteel supports several such strengthening profiles and can determine the torsional stiffness to be considered in preventing or limiting warping.
Analysis with Consteel Superbeam
Let’s take the following case. We have a simple supported 5 m long beam loaded by a uniform load of 20 kN/m acting at the top flange, on top of its self weight, without any intermediate lateral support. Its section is a welded I profile, made of S235, 10 mm thick plates, flange width of 200 mm and total section depth of 320 mm.
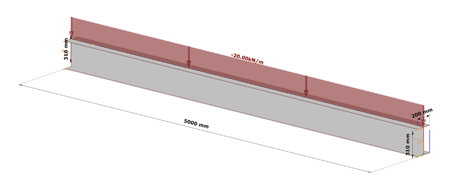
As we can expect, in the case of such a large unbraced length, the bending moment resistance would be strongly limited by lateral-torsional buckling, and therefore we can expect that strengthening by the proposed method is viable.
The critical moment of this beam is obtained in Consteel using linear buckling analysis with 7DOF beam elements option of the Superbeam, which has found the critical multiplier of 2.88.
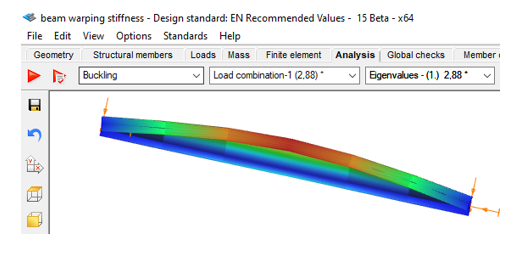
This results Mcr = 2.88*64.18=184,84 kNm and a slenderness λ of 1,036 and reduction factor of 0,519.
The final bending moment resistance is 103 kNm.
Let’s further assume that this resistance needs to be increased by 30% due to new requirements. Let’s see whether a successful strengthening without modifications of the cross-section would be possible.
gateIntroduction
Beam with welded I sections are often executed with slender webs. This is mainly due to the recognition that the main contributors to bending stiffness of a beam are the flanges. The web plate’s main role is to safely keep these flanges away from each other and carry the shear stresses which might be present. Significant weight saving can be achieved with the use of slender webs, but there are some aspects to take care about.
When slender web plates are exposed to longitudinal, uniform normal stresses, above a certain stress level its distribution will no longer remain uniform. A compressed region of a plate distant from its lateral supports may buckle in a direction perpendicular to the acting external normal stresses, causing a subsequent transfer of stresses from the affected region to other neighbouring regions remaining in their unbuckled position.
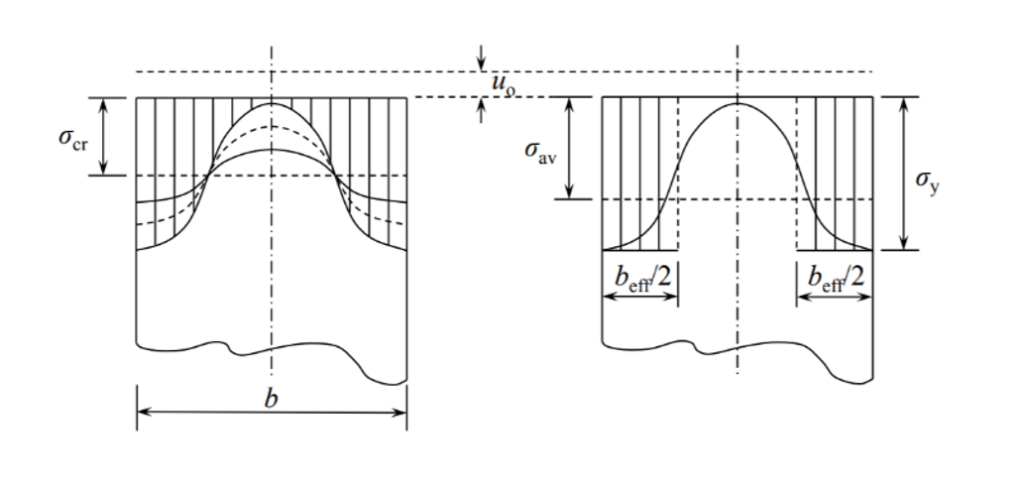
This buckling remains limited to a part of the plate keeping other parts intact and therefore is called as local buckling. Local buckling usually does not result an immediate collapse of the structure, due to possibility of the stresses to redistribute and often even a substantial amount of further load increases are possible.
The tendency of a compressed plate to suffer local buckling is characterized by its slenderness value defined by the following formula
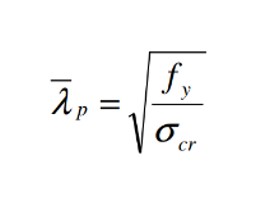
where σcr is the critical stress level above of which the stress redistribution and local buckling starts to appear. A higher critical stress will result in lower slenderness value which indicates that the plate can carry higher compressive stresses without the initiation of local buckling.
Analysis of cross-sections with beam finite elements
The well-known beam finite elements used by usual structural design software do not “see” the internal composition of the cross-section. During structural analysis the sections are represented by certain integrated cross-sections properties assuming the validity of several assumptions including the Bernoulli-Navier Hypothesis and the non-deformability of the cross-section. A local buckling of any of its internal plates would violate these assumptions making hard to create the equivalent cross-sections properties.
In the modern design practice followed by Eurocode the phenomenon of local buckling is handled by the use of effective section properties. Regions subject to possible local buckling of compressed plates of a cross-sections are “eliminated” and the section properties are calculated based on the remaining parts of the cross-sections.
Design verifications use these effective cross-section properties to calculate the resistance of cross-sections exposed compressive forces. When required by Eurocode, the effect of appearance of local buckling can also be reflected in a structural analysis using beam finite elements with the use of effective cross-section properties, instead of the original gross section properties. This is mainly required to prove serviceability criteria.
Analysis of cross-sections with Consteel Superbeam
The Consteel Superbeam function makes possible to confirm directly the presence of local buckling using the same beam element based model, but using a mixed beam and shell finite element modelling and analysis approach. Using the Superbeam tool, complete structural members or parts of them can be alternatively modelled with shell elements and the rest can still be modelled with beam finite elements. Using this technique, the total degrees of freedom of the model can be kept as low as possible. When using Superbeam, the designer has the choice whether to use beam or shell finite elements, as appropriate.
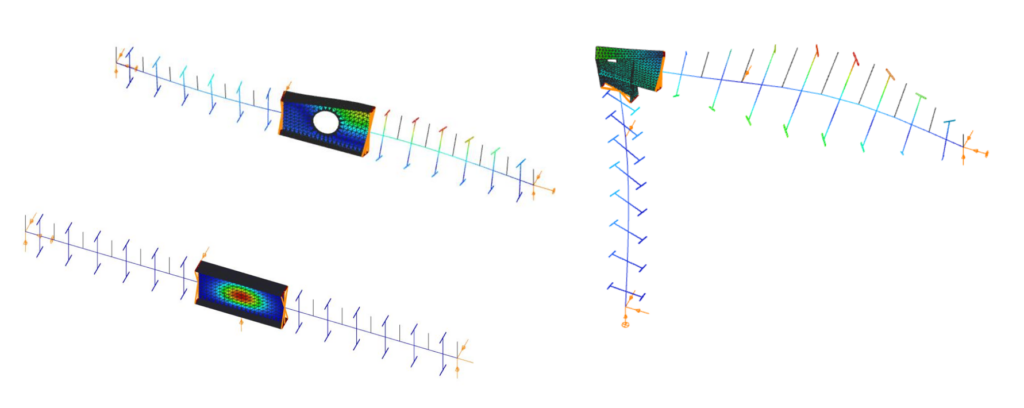
Contrary to beam finite elements, modelling with shell finite elements doesn’t have the previously mentioned limitations. This approach can fully consider the shape and location of the cross-section’s internal components instead of the use of an integrated overall section property. When a linear buckling analysis (LBA) is performed, the critical stress multipliers corresponding to the actual stress distribution can be obtained. Additionally to the load multipliers, the corresponding buckling shapes are also available, giving direct indication on the location, shape and appearance of local buckling within the compressed parts of the cross-section.
The use of effective cross-section concept is very convenient but there might be cases when more insight view is desired. The following example gives an idea where the Superbeam function can be helpful.
Demonstrative example
Let’s consider a 12 m long simple supported welded beam with the following parameters
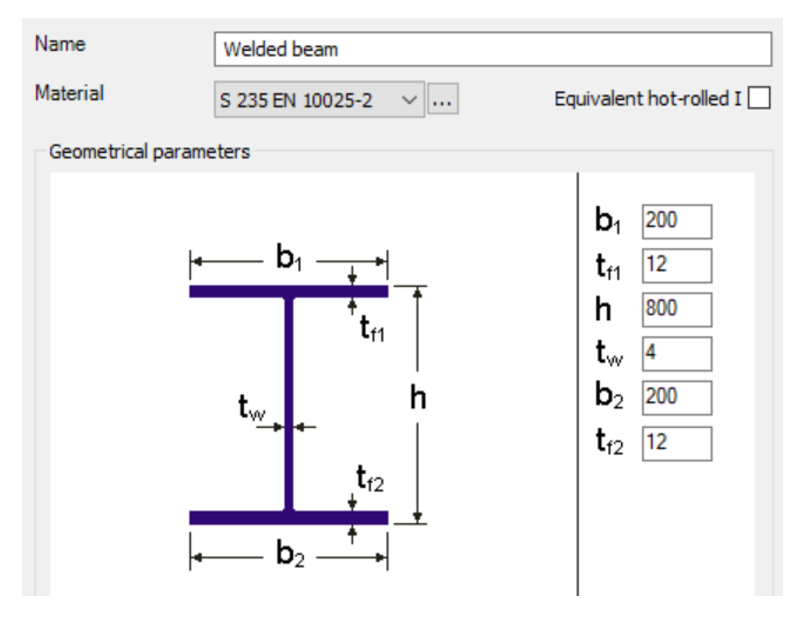
The beam is laterally restrained at third points at the level of its upper flange. The beam is loaded with its self-weight plus a uniformly distributed load of 10 kN/m acting at the level of upper flange.
When the beam is analysed with 7DOF beam finite elements, one can obtain the critical load multiplier of 5.2 of the global buckling mode, which is lateral-torsional buckling (LTB) in this case.
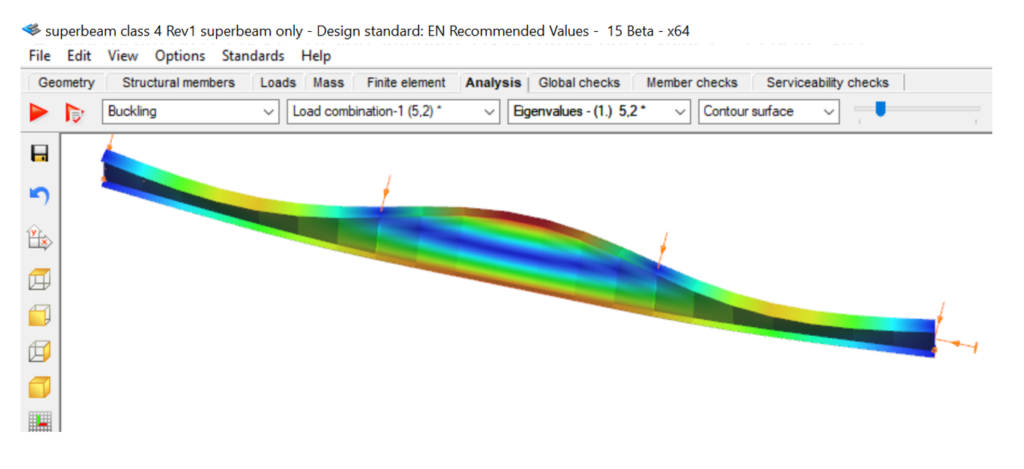
The beam finite element cannot give any visible indication about possible local buckling in compressed plates of the cross-sections.
As the maximum bending moment occurs in the middle third of this beam, it seems enough to analyse this part mode deeply with the Superbeam function. An LBA with the mixed beam and shell model gives comparable critical multiplier of 5.22 with some numeric perturbances in the part modelled with shell elements.
gateIntroduction
Are you wondering how a web opening would influence the lateral-torsional buckling resistance of your beam? Check it precisely with a Consteel Superbeam based analysis
It is often required to let services pass through the web of beams. In such cases the common solution is to provide the required number of opening in the webplate. Such an opening can have a circular or rectangular shape, depending on the amount, size and shape of pipes or ventilation or cable trays.
Beams must be designed to have the required against lateral-torsional buckling. The design procedure defined in Eurocode 3 is based on the evaluation of the critical bending moment value which provides the slenderness value, needed to calculate the reduction factor used for the design verification.
There is no analytical formula provided in the code for beams with web openings. Would the neglection of such cutouts cause a miscalculated and unsafe estimation of the critical moment value?
The following demonstration will be made with a 6 meters long simple supported floor beam with a welded section.
Exposed to a linear load of 10 kN/m, the critical bending moment value of the solid web beam can be obtained by performing a Linear Buckling Analysis (LBA) with Consteel.
The obtained critical multiplier for the first buckling mode is 3.00 which means that the actually applied load intensity can be multiplied by 3.00 to reach the critical load level. The corresponding critical moment will have the value of Mcr = 3.0 * 47.18 = 141.54 kNm yielding a slenderness of 1.286 (Mpl,Rd = 234.20 kNm) and a lateral-torsional buckling resistance of 0.394 * 234.20 = 92.27 kNm. With this value the actual utilization ratio is at 51%.
How would this value change if a rectangular opening needs to be cut into the web of this beam?
Analytical formula for critical bending moment
By looking to the analytical formula (ENV 1993-1-1 F.4) to calculate the critical moment of double symmetric sections loaded at eccentric load application point it becomes obvious that the section properties having effect on the moment value are Iz, Iw and It.
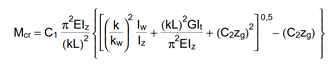
An opening in the web has no effect on the first two values and has very little effect on the last one. As it has been already shown in previous article, the presence of such an opening can have effect on the vertical deflection, but as long as the lateral stiffness of a beam is much lower than it’s strong axis stiffness, the vertical deflections can be neglected when the lateral-torsional buckling resistance is calculated. The usual linear buckling analysis (LBA) performed also by Consteel neglects the pre-buckling deformations.
Therefore one can expect that in general web openings can be disregarded when the critical moment value is calculated.
Analysis with Consteel Superbeam
Beam finite elements cannot natively consider the presence of web openings. In order to obtain the precise analysis result, it is possible to use shell finite elements. The new Superbeam functionality comes as a solution in such cases. Instead of using beam finite elements, let’s use shell elements!
Opening can be positioned easily along the web, either as an individual opening or as a group of openings placed equidistantly. The opening can be rectangular, circular or even hexagonal. Circular openings can be completed with an additional circular ring stiffener.
The rectangular opening for this example can be easily defined with this tool. As there is no need to provide any additional opening on the remaining part of the beam, only the first part which includes the opening will be modelled with shell elements and the rest can still be modelled with beam finite elements. Using this technique, the total degrees of freedom of the model can be kept as low as possible. When using Superbeam, the designer has the choice whether to use beam or shell finite elements, as appropriate.
gateWeb openings and their deflection effect on beams
It is often required to let services pass through the web of beams. In such cases, the common solution is to provide the required number of openings in the web plate. Such an opening can have a circular or rectangular shape, depending on the amount, size and shape of pipes or ventilation or cable trays.
If the structural engineer has the freedom to position these openings along the beam, where to place them? What would be its effect on the deflection of the beam?
The effect of such openings on the deflection is more important when the length of the opening along the beam is increased. As circular openings are made with equal length and depth, they are usually less critical than rectangular openings.
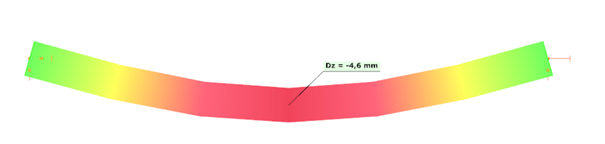
The following demonstration will be made with a 6 meters long simple supported floor beam with a welded section.
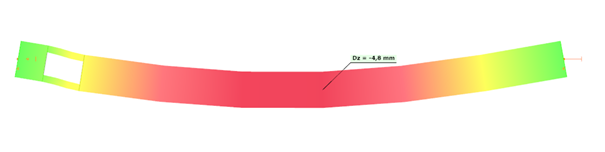
Exposed to a linear load of 10 kN/m, the deflection at mid-span of the solid web beam is 4.6 mm.
Let’s assume that a 250 mm deep rectangular opening with a length of 400 mm needs to be provided on the web, at a distance of 300 mm from the left support.
Traditional analysis with beam finite elements
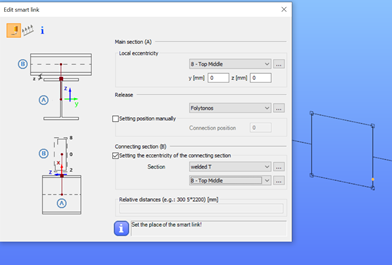
Consteel 7DOF beam finite elements are very powerful, but cannot consider natively such opening. The usual approach is to build a Vierendeel-type of model, by using additional beam elements with a T shape section „above” and „below” the opening. These additional beam elements are defined eccentrically to the reference line of the solid-web beam.
Eccentricities can be easily defined in Consteel using both smart and traditional link elements.
The deflection with this refined model will be equal to 4.8 mm.
Analysis with Consteel Superbeam – use shell elements for more precise analysis results
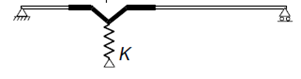
gateIn our series we have shown in Part 1 and Part 2 how the spring stiffness „K” is determined for and edge and for an intermediate stiffener. In this part we will show how to proceed further.
The goal is to determine how efficiently can this stiffener support the connected compressed plate. To consider local buckling of the compressed plate the effective widths will be calculated. These widths can be either calculated for a plate supported at both ends or for a plate supported at one end only, using Table 4.1 and Table 4.2, respectively.
If a stiffener fulfills the minimum constructive requirements, we will first assume that it is rigid enough the act as a support. Based on this we work out the effective lengths for the connected compressed plates, assuming also that they are fully loaded up to the yield strength. Once we know the effective widths of the plate parts connected to the stiffener, we also know the load this stiffener is supposed to be able to carry without buckling, to justify the first assumption. Therefore, next we calculate the flexural buckling resistance of the stiffener. If we find out that it is lower than what was implicitly assumed previously, we go back to the first step, lower the stress to be compatible with the obtained buckling resistance of the stiffener (distortional buckling). This lower stress level may of course result different effective widths. An iterative procedure is started until the satisfactory result is found. After completion the final stiffener buckling resistance value will be incorporated into an equivalent effective thickness applicable for the stiffener and the connected effective plate parts.
In the above described iterative process the „K” value of the stiffener will be needed to determine the flexural buckling resistance of the stiffener. This resistance will be calculated using the help of a simple beam model, where the stabilization provided the remaining parts of the section is used as a continuous bedding of „K”. The cross section of the beam corresponds to the stiffener and connected plate parts and will be exposed to the actual stress level of the iteration, assumed as a simplification to be constant along the length. The length of the beam in this model is unknown at the moment, it should be equal to the half wavelength of the buckling shape which is expected to be around 1.5-3 times the height of the studied cold-formed section.

Distortional buckling will appear only if the length of the stiffener is much longer than this typical length range. As a further simplification Eurocode assumes infinite length as the possible worst case, because for this condition an analytic solution exists in the literature:
In this formula „K” is the spring value – shown in Part 1 and Part 2 – represents the spring stiffness value what the remaining section can provide to the stiffener. Isand Asare section properties of the corresponding stiffener together with connected effective widths of supported plates, namely area and inertia around an axis perpendicular to the expected direction of buckling of the stiffener. E is the Young modulus of the steel material.
The formula gives the critical stress level where elastic buckling would appear. Once this has been found, reduced slenderness is calculated, and the distortional buckling resistance can be obtained by using a special buckling curve given by (5.12a-c) formulas of EN 1993-1-3.
The validity of formula (5.15) can be easily demonstrated with a simple Consteel model.
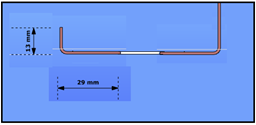
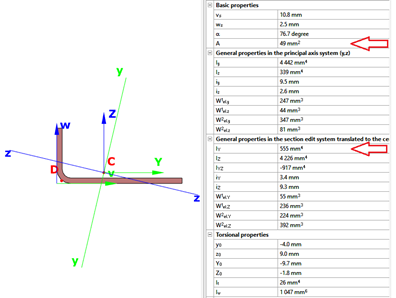
Let’s assume the Z section from our 1st blog exposed to compression force and let’s assume that we have already calculated effective width values. Yield strength of the material is 235 MPa and coating thickness is 0.04 mm. We found that the effective width of the lip and flange are ceff=13 mm and beff=29 mm, respectively.
The section properties can be calculated with Consteel
gateDistortional buckling – Further secret formulas of EN 1993-1-3. Check our article for the first secret formula if you hadn’t read it yet.
In our series we continue with the second „secret” formula of EN 1993-1-3.
This formula (5.11) is used when the ability of an intermediate stiffener to stabilize a compressed web plate is studied.
When the intermediate stiffener is rigid enough, it divides efficiently the longer web plate into shorter plates. During buckling a rigid stiffener will not displace and the plate will buckle between the ends (stabilized by flanges) and this stiffener:
If the stiffener is not rigid enough, already at a much lower stress level the distortional buckling will appear which is characterized by a displacement of the stiffener and by the web plate buckling with a half-wave equal to the plate length:
In such a case Eurocode still accepts that web plate buckling will occur between ends and intermediate stiffener, but reduces the thickness of the intermediate stiffener zone, to compensate for the less than ideal rigidity. This compensation will depend on the buckling resistance of the stiffener when subject to compression.
The simplified model used by Eurocode in the procedure can be seen below. As a simplification it is assumed that the web plate is connected to the rest of the section with hinges. It means that it’s buckling shape is not influenced by the stiffness of connected parts, they do not encaster its ends, its ends can freely rotate. The ends of the plate are supported and there the plate can provide an elastic bedding to the stiffener, which will be considered as a „help” when its buckling resistance will be determined. This bedding is represented by the K spring stiffness:
The spring value which represents in this model the bedding provided by the plate is calculated as the ratio of the displacement obtained from the application of a unit load at the center of gravity of the stiffneer. In this case the unit load is applied perpendicularly to the web plate. Formula (5.11) gives the deflection (δ) from such unit load (u).
gate