Rácsos tartó rúdjainak kihajlási hossza
Rácsos tartó szerkezet méretezése
A rácsos tartók globális (rúdszerkezeti szintű) méretezése nem igényel különleges elméleti ismeretet: rendszerint a hajlítónyomatékok és a nyíróerők elhanyagolásával a rácsos tartók rudjait nyomott és/vagy húzott rúdként méretezzük. A nyomott rudak méretezését manapság modell alapú számítógépes eljárással hajtjuk végre. Ennek részleteit lásd a Nyomott rúd méretezése kihajlás ellen című tudásbázis anyagban. Itt csak a nyomott rudak kihajlási hosszának meghatározását mutatjuk be.
A nyomott rúd méretezésénél a legfontosabb paraméter a rúdkarcsúság:
$$\overline{\lambda}=\sqrt\frac{Af_y}{N_{cr}}$$
ahol
$$N_{cr}=\frac{\pi^2El}{(kL)^2}$$
ahol a k kihajlási hosszt (befogási tényezőt) az EN1993-1-1 szabvány, a kézi számítások megkönnyítése érdekében, az alábbiak szerint javasolja felvenni:
| Nyomott rúd típusa | Kihajlás iránya | k |
|---|---|---|
| övrúd | - tartó síkjában - tartó síkjára merőlegesen | 0.9 0.9 |
| rácsrúd | - tartó síkjában - tartó síkjára merőlegesen | 0.9 1.0 |
A modell alapú számítógépes eljárásokon alapuló szoftverek (pl. a Consteel szoftver) a fenti konzervatív szabály helyett az Ncr rugalmas kritikus erőt közvetlenül végeselemes numerikus módszerrel, a teljes rácsos tartó viselkedésének figyelembe vételével, határozzák meg. Az alábbi példával a szabvány által javasolt kézi méretezési eljárás és a modern, modell alapú numerikus eljárás eredményének viszonyát kívánjuk szemléltetni.
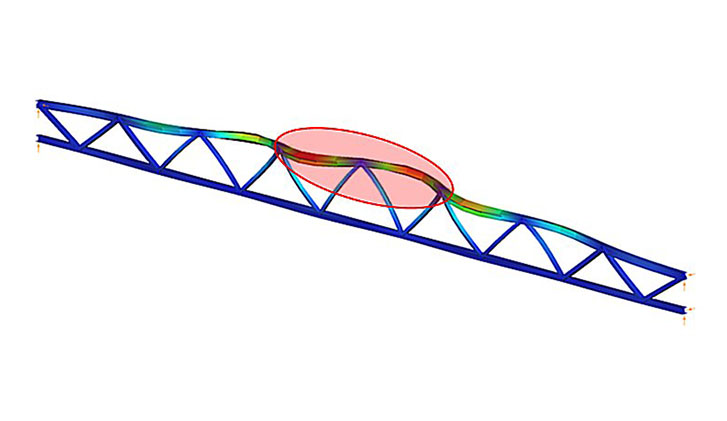
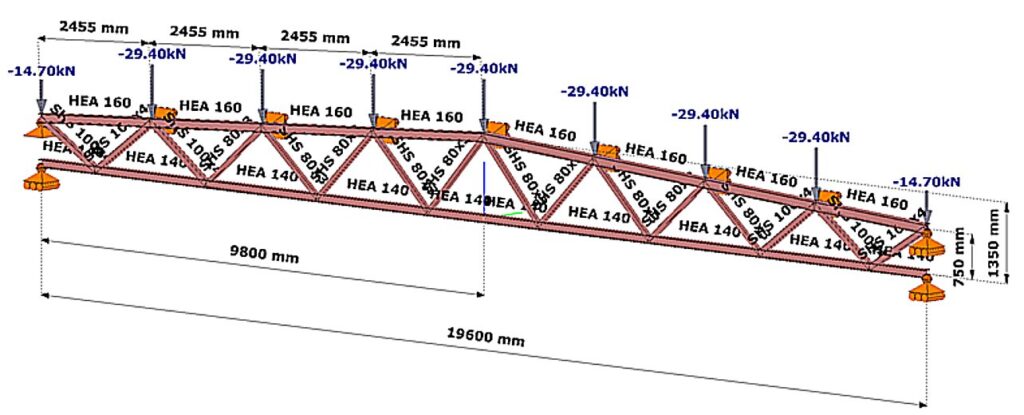
- Legyen a vizsgált rácsos tartó szerkezeti modellje az 1. ábrán látható Consteel modell.
- A feltűntetett teher feleljen meg a tartó mértékadó tervezési teherkombinációjának.
- Határozzuk meg a legjobban igénybe vett nyomott övrúd kihajlási hosszát végeselemes numerikus stabilitási analízis segítségével.
(Consteel szoftver)
Eljárások összehasonlítása
A számítás lépései a következők:
Rugalmas stabilitási analízis
A rugalmas modell stabilitási analízise megmutatja, hogy a rácsos szerkezet mértékadó stabilitásvesztési módját és az ahhoz tartozó αcr rugalmas kritikus teherszorzót (2. ábra).
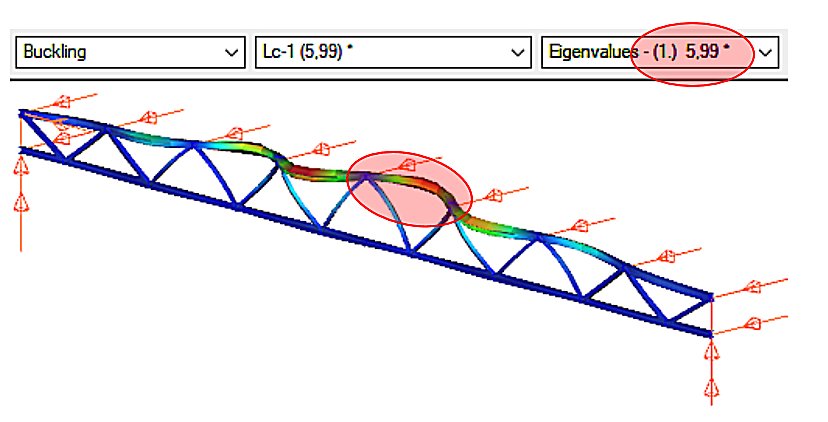
Láthatjuk, hogy a terhelés hatására a tökéletesen rugalmas modell felső öve oldalsó irányban kihajlást szenved. A teher, amely hatására a rugalmas kihajlás bekövetkezik, a kritikus teher, amelynek értékét a tervezési teher és az αcr=5.99 kritikus teherszorzó szorzata adja meg.
Log in to view this content
Online service access and support options are based on subscription plans. Log in to view this content or contact our sales department to upgrade your subscription. If you haven’t tried Consteel yet, try for free and get Pro access to our learning materials for 30 days!