Superbalken für Trägerberechnung bei Querschnittklasse 4
Einführung
Geschweißte I-Profile besitzen häufig schlanke Stege, um große Biegetragfähigkeiten infolge weit gespreizter Flansche zu erreichen. Der Steg trägt dann vorwiegend die Schubspannungen. Damit können signifikante Gewichtsersparnisse erzielt werden, aber dem Stegverhalten ist besondere Aufmerksamkeit zu schenken.
Wenn schlanke Stege mit konstanten Normalspannungen beansprucht werden, entsteht mit steigender Spannung eine ungleichmäßige Spannungsverteilung. Die am weitesten von den gehaltenen Längsrändern (Übergang Steg/Flansche) entfernte Region beult senkrecht zur Stegfläche aus, wobei sich die Spannungen vom ausgebeulten Bereich in die Nachbarbereiche verlagern und die Spannungen dort vergrößern.
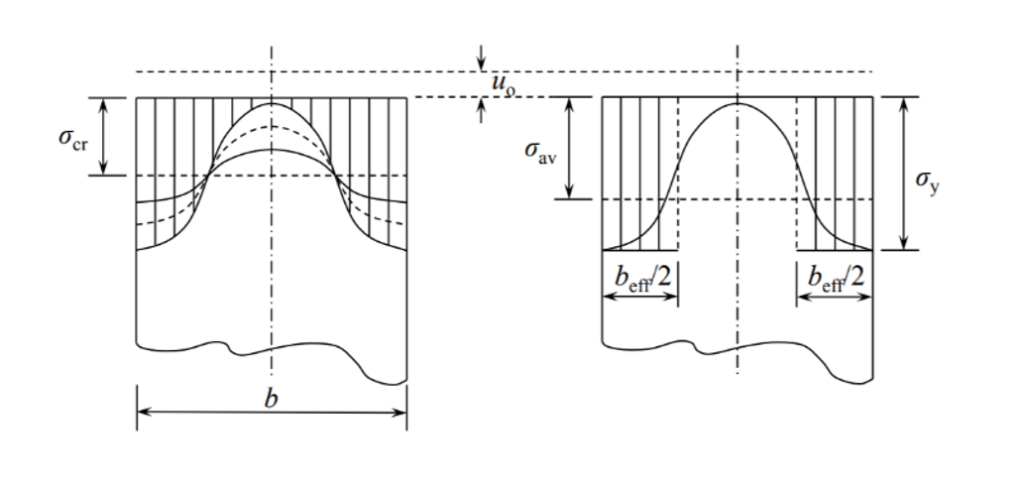
Der ausgebeulte Bereich bleibt lokal begrenzt und die Nachbarregionen bleiben tragfähig, sodass man von „lokaler Beulung“ spricht. Dieses Verhalten führt nicht zu einem unmittelbaren Kollaps, da sich die Spannungen in die steiferen Stegbereiche verlagern können und oft sogar noch eine erhebliche Spannungssteigerung erlaubt ("überkritischer“ Bereich, der nur mit Theorie 3. Ordnung berechenbar ist).
Die Beulgefahr einer gedrückten Platte (Steg) wird mit ihrer Schlankheit gekennzeichnet, die mit der folgenden Formel berechnet wird:

mit σcr als kritisches Spannungslevel, bei der die lokale Beulung mit Spannungsumlagerung beginnt.
Berechnung mit Querschnitten der finiten Balkenelemente
Alle finiten Balkenelemente beliebiger Berechnungssoftware für Strukturen wissen nichts von der internen Komposition der Balkenquerschnitte, denn diese werden durch abstrakte numerische Angaben wie Fläche, Trägheitsmomente, etc. erfasst. Dazu werden einige Annahmen wie z. B. die Bernoulli-Navier Hypothese und das Ebenbleiben der Querschnitte getroffen. Das lokale Beulen eines Querschnittbereiches würde diese Annahmen verletzen und es schwierig machen, äquivalente numerische Querschnitteigenschaften anzugeben.
Die moderne Nachweispraxis des EC's erfasst das lokale Beulen mittels der effektiven Querschnitteigenschaften. Beulgefährdete gedrückte Querschnittbereiche werden „eliminiert“ und die Querschnitteigenschaften des nunmehr „gelochten“ und meist unsymmetrischen Querschnitts werden am Restquerschnitt ermittelt.
Die EC-basierten Tragfähigkeitsnachweise gedrückter Querschnitte berücksichtigen die effektiven Querschnittswerte der Klasse 4. Aber falls der EC es verlangt, kann das lokale Beulverhalten auch bereits bei der Berechnung der Beanspruchungen mit Balkenelementen, die die effektiven Querschnittseigenschaften anstelle der Bruttoquerschnittswerte verwenden, berücksichtigt werden. Hauptsächlich kommt dies bei den Gebrauchstauglichkeitsnachweisen vor.
Querschnittsanalysen mit dem ConSteel Superbalken
Die ConSteel-Funktion „Superbalken“ ermöglichst auf direktem Wege die Berücksichtigung lokaler Beulen. Ein mit Superbalken auf einfache Weise konstruiertes Modell besitzt (zunächst unsichtbar) sowohl eine Balken- als Schalenelementierung und benutzt zugehörige Berechnungsmethoden. Mit dem Superbalken-Tool können komplette stählerne Strukturen oder Teile davon alternativ mit Schalenelementen und der Rest der Struktur mit Balkenelementen modelliert werden. Eine geschickte Nutzung dieser Technologie kann die Anzahl der Verformungsfreiheitsgrade des Gesamtmodells und damit die erforderlichen Rechenzeiten extrem reduzieren. Denn mit dem Superbalken hat der Tragwerksplaner die Wahl, ob (global oder lokal im Modell) Balken- und/oder Schalenelemente verwendet werden sollen.
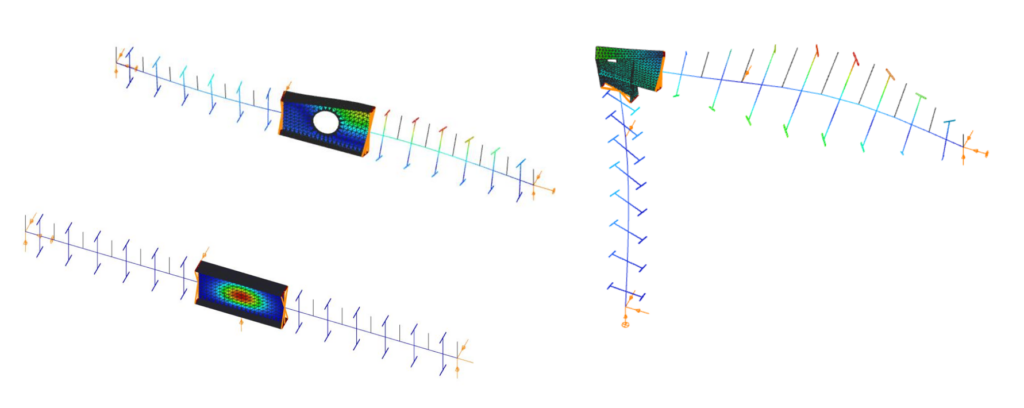
Im Gegensatz zu Balkenelementen hat die Modellierung mit Schalenelementen keine Einschränkungen bei der Querschnittsmodellierung. Diese Vorgehensweise berücksichtigt das Verformungsverhalten der einzelnen Querschnittskomponenten anstelle der Verwendung integraler numerischer Querschnittswerte der Balkentheorie. Bei linearen Stabilitätsanalysen erhält man die kritischen Spannungsmultiplikatoren, die mit der Spannungsverteilung korrespondieren. Zusätzlich ergeben sich die Eigenformen, die unmittelbar die Lage, Form und das Auftreten lokaler Beulen innerhalb der gedrückten Querschnittsbereiche.
Das Konzept effektiver Querschnittswerte der Balkentheorie bei Querschnitten der Klasse 4 ist baupraktisch zufriedenstellend, aber es können Fälle auftreten, bei der vertiefte/genauere Erkenntnisse erforderlich sind. Das folgende Beispiel illustriert, wann der Superbalken hilfreich sein kann.
Demonstrationsbeispiel
Es wird ein 12 m langer beidseitig gabelgelagerter Schweißträger mit den folgenden Querschnittswerten betrachtet.
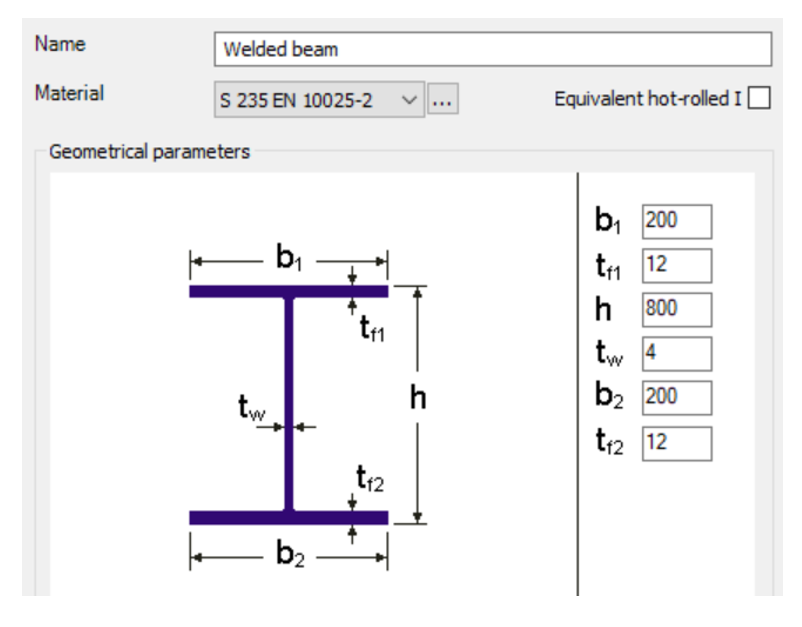
Der Balken wird seitlich horizontal in den Dritteispunkten am Oberflansch starr gestützt. Die Einwirkung besteht aus Eigengewicht plus einer mittig am Oberflansch angreifenden konstanten Linienlast von 10 kN/m.
Die Stabilitätsberechnung mit finiten Balkenelementen und den Bruttoquerschnittswerten (ohne Berücksichtigung der Querschnittsklasse 4 im Steg) führt zu dem kritischen Laststeigerungsfaktor alfa-crit=5,2. Die zugehörige Eigenform zeigt in diesem Fall globales Biegedrillknicken.
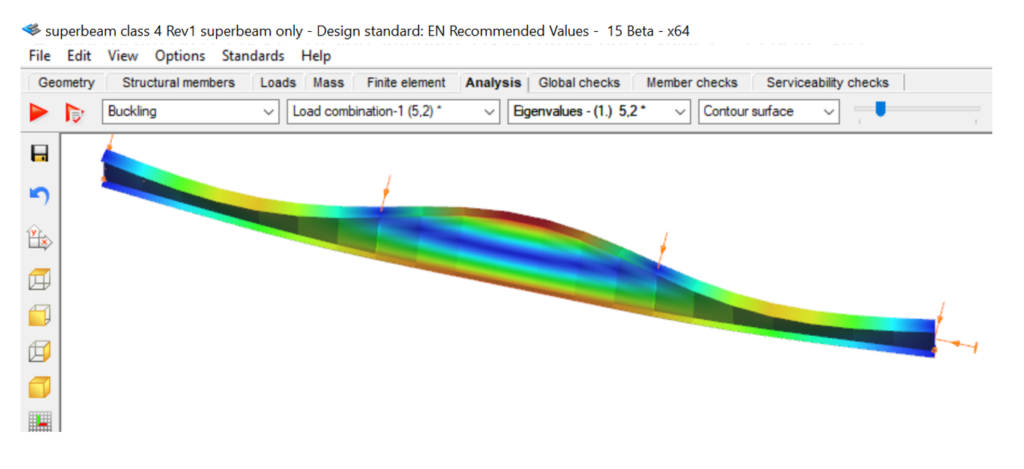
Die Berechnung mit finiten Balkenelementen gibt keinerlei Hinweise für ein mögliches Auftreten lokaler Beulen in den gedrückten Querschnittsbereichen.
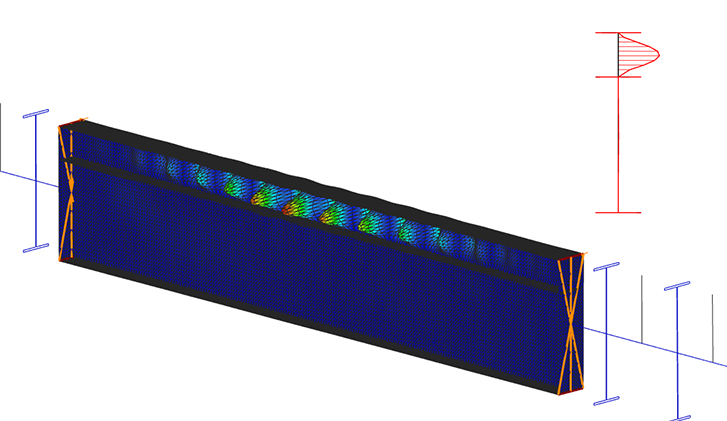
Da das maximale Biegemoment im mittleren Drittel erscheint es sinnvoll, nur diesen Bereich des Trägers mit der Schalenelementierung des Superbalkens zu elementieren. Die lineare Eigenanalyse mit dem gemischt elementierten Modell führt zu dem kritischen Laststeigerungsfaktor alfa-crit=5,22 des globalen Biegedrillknickens, was nahezu identisch zu den Berechnungen mit reiner Balkenelementierung ist. Die zugehörige Eigenform zeigt allerdings Verformungsstörungen im gedrückten Stegbereich der Schalenelementierung.
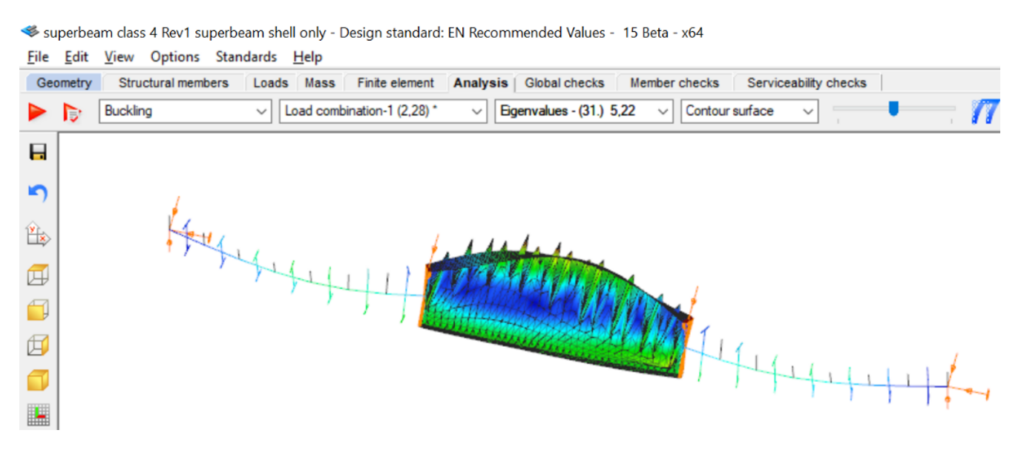
Zusätzlich zu der globalen Eigenform kann das mit dem Superbalken modellierte Modell auch das reale lokale Beulverhalten im mittleren Bereich des Trägers erfassen. Die zum niedrigsten berechneten Eigenwert alfa-crit=2,28 gehörende Eigenform zeigt klar das lokale Beulmuster im Bereich der größten Biegedruckspannungen im mittleren Trägerbereich.
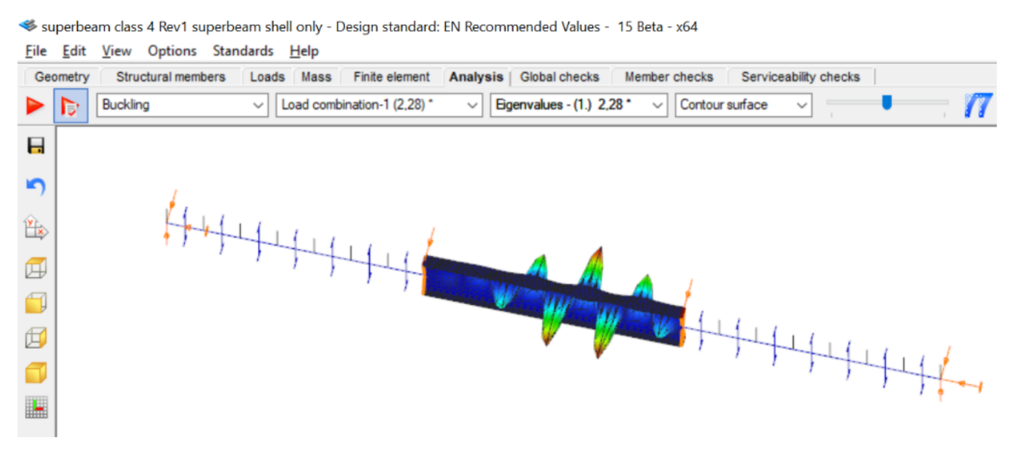
In der folgenden Seitenansicht der Eigenform des Trägers erkennt man sehr gut, dass sich die maximalen Ordinaten der lokalen Beulen ungefähr in der Mitte der oberen Hälfte des druckbeanspruchten Steges befinden.
(Hinweis: die roten Linien stellen die von ConSteel automatisch benutzten Zwangsselemente im Übergangsquerschnitt von der Schalen- zur Balkenelementierung dar).
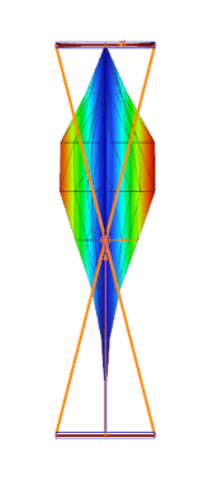
Derartig in der elastischen Eigenform auftretende lokale Beulen bedeuten nicht automatisch, dass der Träger mit seinem schlanken Steg unter Ansatz von effektiven (reduzierten) Querschnitten nachzuweisen ist. Effektive Querschnitte sind zu verwenden, wenn der in DIN EN 1993-1-5 mit Formel (4.2) definierte Reduktionsfaktor ρ für gedrückte Querschnittsbereiche kleiner als 1,0 ist. Dies ist der Fall, wenn die Plattenschlankheit λp (s.o.) Werte größer als 0,673 annimmt.
In unserem Beispiel beträgt die maximale elastisch berechnete Druckspannung an der Stegoberkante 82,52 N/mm2 und damit berechnet sich die niedrigste kritische Spannung im Beulbereich zu 2,28 · 82,52 = 188,15 N/mm2. Das führt zu einer Plattenschlankheit λp=1,12 mit fy=235 kN/mm2 und dem Reduktionsfaktor ρ=0,811.
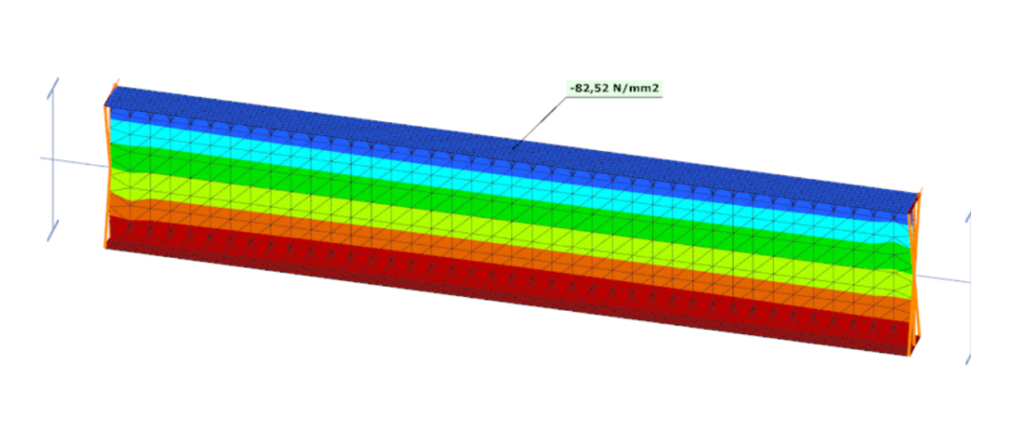
Diese Kontrollrechnung bestätigt einen sehr schlanken Steg, der nicht in der Lage ist, die im Bruttoquerschnitt berechneten Biegedruckspannungen zu ertragen und damit ist der Querschnittsteg in die Klasse 4 einzustufen und muss folglich mit effektiven Querschnittswerten nachgewiesen werden.
Das folgende Bild zeigt den mit ConSteel-Balkenelementen berechneten effektiven Nettoquerschnitt mit Loch im oberen Bereich des Steges.
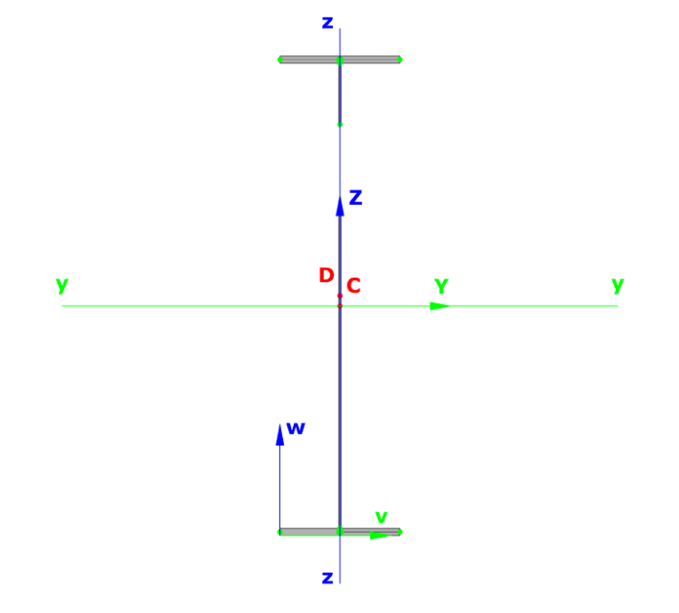
Wie kann eine solche Querschnittsreduktion vermieden werden?
Zum Beispiel kann die Anordnung einer genügend starken Längssteife in etwa in der Nähe der maximalen Ausbiegung der Beule angeordnet werden, mit der Erwartung, dass das Beulverhalten reduziert oder gar vollständig verhindert wird. Zur Steigerung der Effizienz können zusätzliche vertikale Steifen am Ende der horizontalen Steife dienen.
Die Standard-Prozedur des Eurocodes zur Bestimmung der effektiven Querschnittswerte bei Querschnittsklasse 4 kann Längssteifen nicht berücksichtigen. Aber Längssteifen – neben anderen Möglichkeiten – können mit einem zusätzlichen Tool der Superbalkenfunktion (auch zusammen mit vertikalen Steifen an beiden Enden des mittleren Drittes des Balken) angeordnet werden.
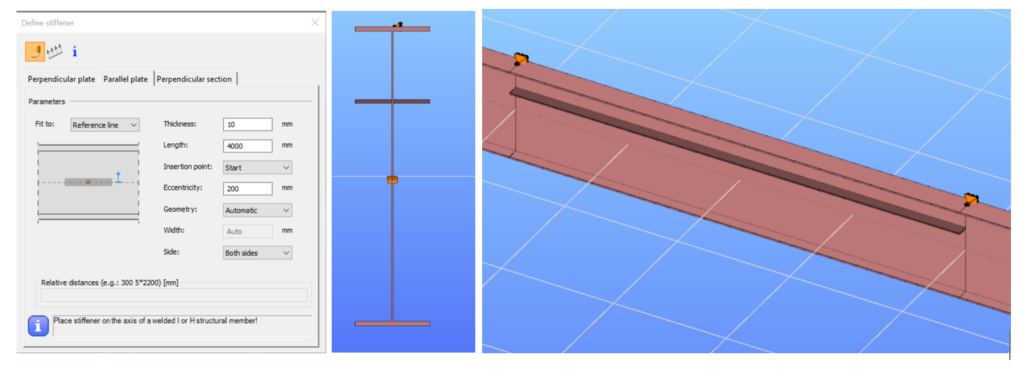
Wenn in unserem Beispiel 10 mm dicke Flachsteifen auf beiden Seiten des Steges etwa im Bereich der maximalen Ordinate der Beulen des Beulmusters angeschweißt werden, führt dies zu einem komplett anderen lokalen Beulverhalten mit alfa-crit=7,72. Das ergibt eine etwa 3,5-fache Steigerung.
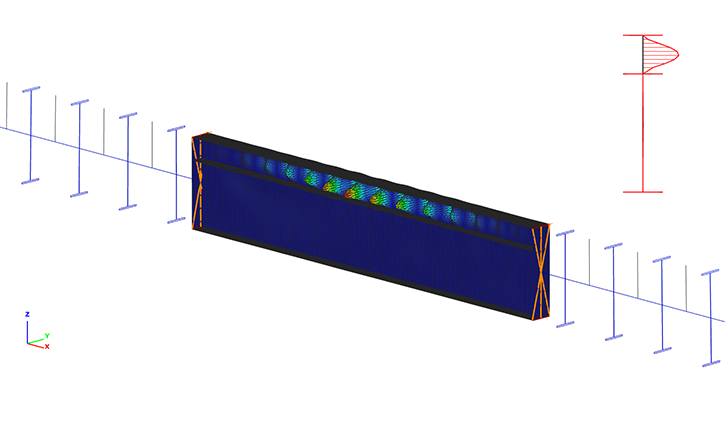
Eine erneute Kontrollrechnung ergibt σcr=7,72 · 82,52 = 637,0 N/mm2 und λp= 0,606 < 0,673. Damit muss kein effektiver Querschnitt gemäß Querschnittsklasse 4 beim Tragfähigkeitsnachweis angesetzt werden.
Es ist hier darauf hinzuweisen, dass die zusätzlich angeordneten Steifen genügend stark ausgebildet sind. In Kapitel 4.5 von DIN EN 1993-1-5 gibt es entsprechende Anweisungen.
Mit dem Superbalken-Analysetool erhält der Tragwerksplaner die Möglichkeit zu vertieften Einsichten in das Tragverhalten seiner Struktur, um möglichst optimale Lösungen stabilitätsbezogener Probleme zu entwickeln.