This study explores how Computational Fluid Dynamics (CFD)–based pressure simulation results can be compared and aligned with wind tunnel experiments and standardized design methods, reflecting the practical process engineers follow when assessing wind loads. The aim is to provide a framework for interpreting and applying simulation outputs with more confidence, supported by a clear workflow. To ensure that the findings are robust and generalizable, the analysis is grounded in a comprehensive parametric dataset: the Tokyo Polytechnic University (TPU) database of isolated low-rise buildings without eaves. This resource contains detailed pressure coefficient data for 116 building models—featuring flat, gable, and hip roofs—tested under eight wind directions, yielding more than 800 individual cases for comparison. To align these wind tunnel tests with the standard procedures the main orthogonal directions were investigated.
Compliance with standards
Before validating CFD results against established references, it is important to set the Eurocode baseline for wind load evaluation. From the wind effect side, a previous article covers how the specific wind profiles are determined and harmonized with the simulations during the preprocess phase, while for wind actions the Eurocode defines two main approaches:
- Wind pressure on surfaces – expressed through pressure coefficients for a range of building geometries.
- Wind forces on special structures – i.e. lattice towers.
Since CFD inherently produces surface pressure distributions, this study focuses exclusively on the first approach—wind pressure on surfaces—applied to closed buildings. For the purposes of this comparison, only vertical walls and simple roof types (flat and duopitched) were considered.
Under Eurocode procedures, building surfaces are subdivided into zones whose dimensions are determined by the building’s proportions. In practice, the characteristic zoning length, e , defines the extent of the regions for which local pressure coefficients are specified.
Therefore, to ensure a coherent comparison between wind tunnel tests and simulation results, the mesh refinement must be adjusted accordingly, for each previously presented geometrical case of the dataset for both principal orthogonal directions, which in turn makes a parametric study indispensable.
Parametric methodology
To support the parametric study, a dedicated script was developed to generate results for all three scenarios simultaneously: wind tunnel tests, simulation outputs, and standard-based approaches.
gateEbben a cikkben egy egyszerű téglatesten alkalmazott nyomásalapú validációt részletezünk a tartószerkezet-mérnöki tervezéshez kapcsolódó szélszimuláció keretében. Az adatfeldolgozásról és a sebességalapú validációról szóló korábbi elemzéseinkre építve célunk, hogy átfogó betekintést nyújtsunk abba, hogyan használhatók a nyomásadatok a szimulációs eredményekből származó szélterhek pontos és megbízható meghatározására.
A nyomásalapú validáció kulcsfontosságú eleme a szélszimulációnak, mivel közvetlenül kapcsolódik a szerkezetekre ható erőkhöz. A korábbi sebességalapú validációk során [1] az eredmények (a sebességvektorok irányváltozásainak átlagos eltérése százalékosan) összehasonlítása a meghatározott referenciaértékekkel azt mutatta, hogy a k-ε turbulenciamodell adta a legjobb eredményeket. Ezúttal viszont ugyanazon szimulációs eredmények felhasználásával nyomásalapú összehasonlítást végzünk.
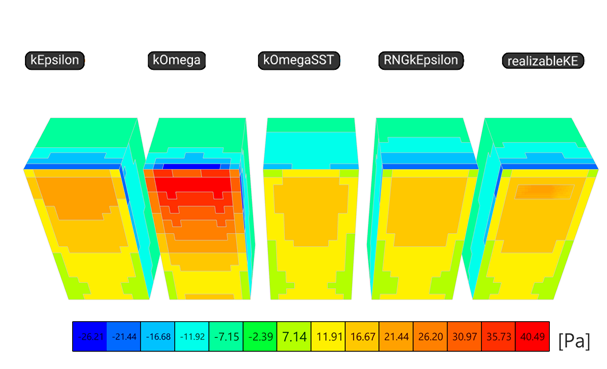
Először is, jelentős különbség van a szimuláció időtartama és az iterációs szám között, amelyet maximum 1000 iterációra volt beállítva. Az alábbi táblázatban látható, hogy a k-ε a leggyorsabb, míg a k-ω SST és az RNGk valójában nem érte el a konvergenciát. A nyomáseredmények alapján számított globális reakciók összehasonlításakor azonban az eredmények viszonylag közel vannak egymáshoz, a felső (Rz) és az oldalfalakon (Ry) lévő szívások esetében több, az Rx esetében (amelyet a széltámadta falon lévő nyomás és a szélárnyékos oldali szívás eredményez) viszont kevesebb, különösen a k-ω esetében.
Megjegyzés: az Ry+ csak a téglatest egyik oldalfalának eredője, mert a másik oldal kioltja, így a globális reakció Ry = 0 kN
| Teher mérete [m] | 4 | ||||
| Turbulencia Modell | k-ε | k-ω | k-ω SST | RNGk | realizable k-ε |
| Időtartam [s] | 135.295 | 392.686 | 707.589 | 663.564 | 440.801 |
| Iteráció [-] | 197 | 413 | 1000 | 1000 | 342 |
| Rx [kN] | 195.63 | 315.59 | 179.88 | 176.23 | 180.22 |
| Ry+ [kN] | 94.54 | 97.75 | 92.98 | 96.95 | 95.73 |
| Rz [kN] | 53.47 | 50.02 | 52.74 | 58.64 | 54.33 |
| ADD [%] | 5.86 | 5.83 | 9.45 | 6.58 | 6.03 |
A megfelelő turbulenciamodellek kiválasztásához és a megfelelő nyomásalapú validáció elvégzéséhez célszerű a témával közvetlenül foglalkozó szélcsatorna-eredmények felhasználása. Ezen a területen Baines egyik legkorábbi, a ma használatos szabványok egyik alapját képező eredménye [2], valamint a Tokiói Műszaki Egyetem viszonylag új, alapos vizsgálata [3] szolgál kiindulópontként.
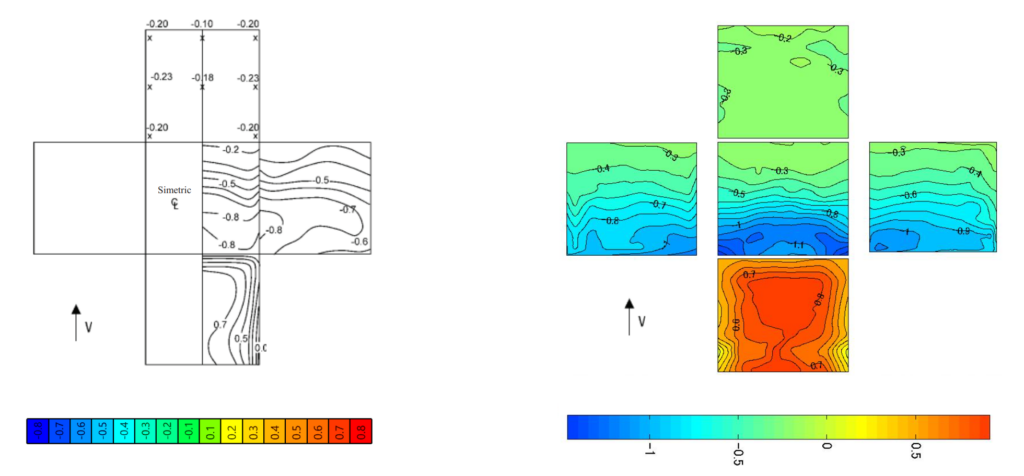
Ezen eredmények feldolgozására speciális eszközök kerültek kifejlesztésre. Baines eredményei adatbázis hiányában az eredeti kép kontúrvonalainak felhasználásával lettek reprodukálva, míg a TPU-kísérlet esetében a tényleges mérési pontok eredményeiből származó átlagos eredményértékeket a Grasshopper parametrikus környezetében lettek feldolgozva.
Megjegyzés: az eredmények megjelenítésének színátmenete nincs harmonizálva a nyomási paraméterek eredményeivel.
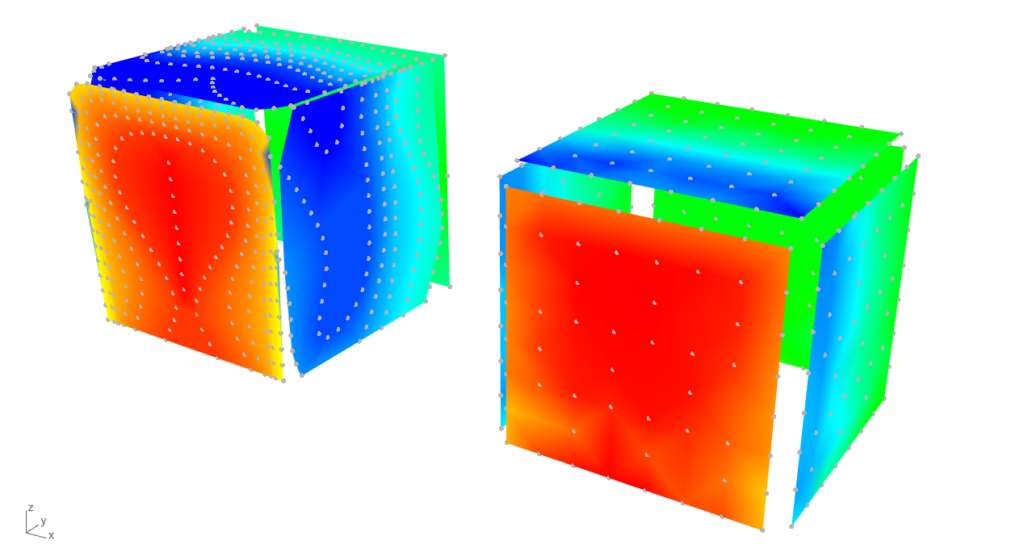
A TPU-eredményekből származó pontok által létrehozott háló átlagos élhosszúságot eredményez a szimulációk végrehajtásának elkezdéséhez. A 16 m x 16 m x 16 m-es kocka esetében a „cellaméret a szerkezeten”, vagyis az élhossz 2,28 m, ami az utófeldolgozásra alkalmas egységes hálót eredményez. A számítási tartomány finomításához r = 2 „hálósűrítéso tényezőt” választottunk, hogy a 16 m-es referenciamagasság alatti bemeneti cellaméretet érjünk el (2,28 x 2r = 9,12 < 16). A szélprofil tekintetében a TPU-kísérlet alapján az Eurocode [4] szerinti III. kategóriájú terepet került kiválasztásra, amely hasonló turbulenciaintenzitású (Iv(zref) = 0,25). A szélsebesség alapértékének vb = 28,3 m/s lett felvéve, hogy qp(zref) = 1 kN/m2 torlónyomást eredményezzen, a nyomási együtthatók (cpe) és a felületi szélterhek (we) közötti könyebb átváltáshoz.
Megjegyzés: az alábbi hat eset eredményére vonatkozó színezés a felületi terhelés eredményei szerint vannak harmonizálva. A félkövér betűvel jelölt értékek a széltámadta, a felső és az egyik oldalsó felületre vonatkozó csúcsértékek (min vagy max), míg a keskeny betűtípus az átlagértéket jelöli. Az elöl lévő tengelyrendszer a felületi terhelések eredőit ábrázolja.
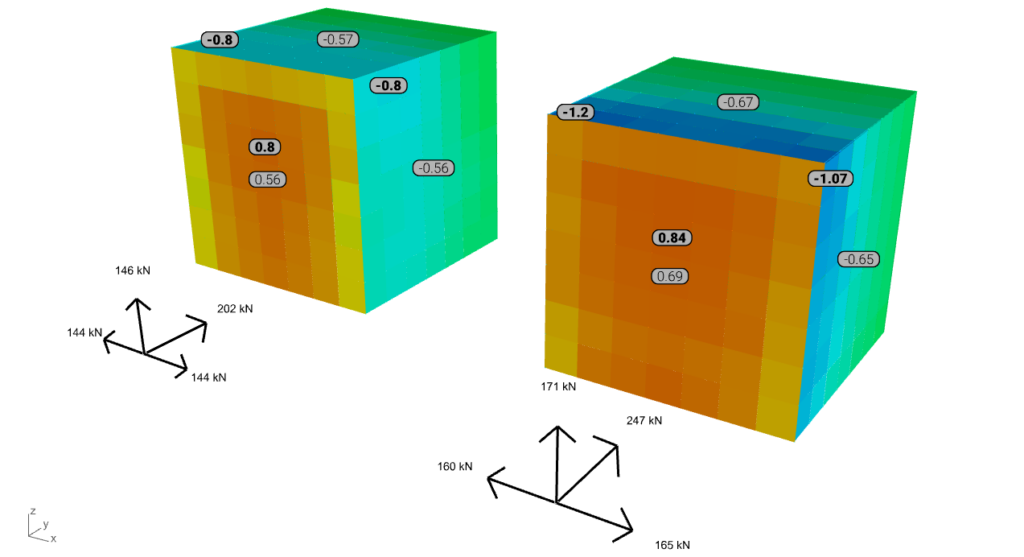
A kísérleti adatokhoz tartozó háló pontjait az utófeldolgozási hálóra közelség alapján történő vetítésekor megfigyelhető volt, hogy a Baines-eredmények általában alacsonyabbak. Ez az eltérés valószínűleg az élek és különösen a sarkok csökkent pontosságának köszönhető. A széltámadta oldalon azonban a maximális nyomástényező megközelítőleg 0,8, míg a szívóerő értékek szintén az Eurocode tipikus értékeihez közelítenek.
A globális reakciók vagy eredők vizsgálatakor a szimulációs eredmények általában megegyeznek a TPU eredményeivel, különösen a széltámadta oldalon. Ezzel szemben a szívott felületek, például az oldalfalak és a tető esetében a szimulációs eredmények átlagosan alacsonyabbak.
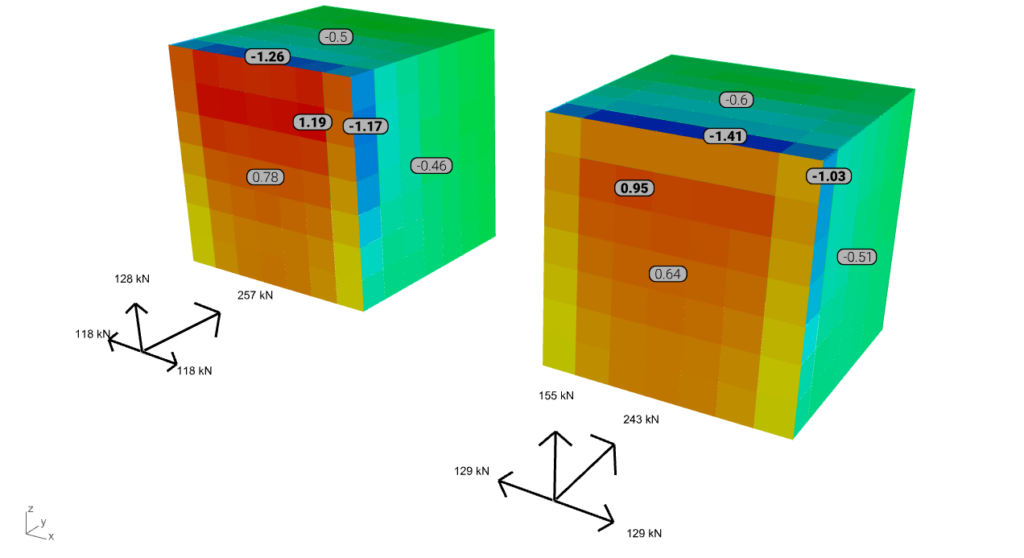
A nyomásalapú validálás szempontjából a k-ω SST nagyobb pontosságot mutat, különösen akkor, ha a szerkezet cellaméretét 1 méterre finomítjuk. Ez a finomítás javítja az eredmények korrelációját, beleértve a szívott oldalakat is. A modell robusztussága azonban megkérdőjelezhető, ami növeli a konvergenciához szükséges számítási időt.
Szerkezeti tervezés szempontjából ezeknek a terheknek a zónázása hatékonyan felhasználható, és a szabványokkal összevethető terheket eredményezhet a szerkezeti elemzés során. Ebből a megközelítésből máris két előnye látható a szimulált terheknek:
- A széltámadta oldalon a szélcsatorna kísérletekhez hasonló megoszlású terhek hozhatók létre, ami egyenletesen megoszló felületi teher helyett csökkentett terhelést eredményez (az Eurocode D zónája).
- Az oldalfalak esetében a terhek magasság menti csökkenése szintén szimulálható, ami az Eurocode A zónáinál kisebb terhelési területekhez vezet.
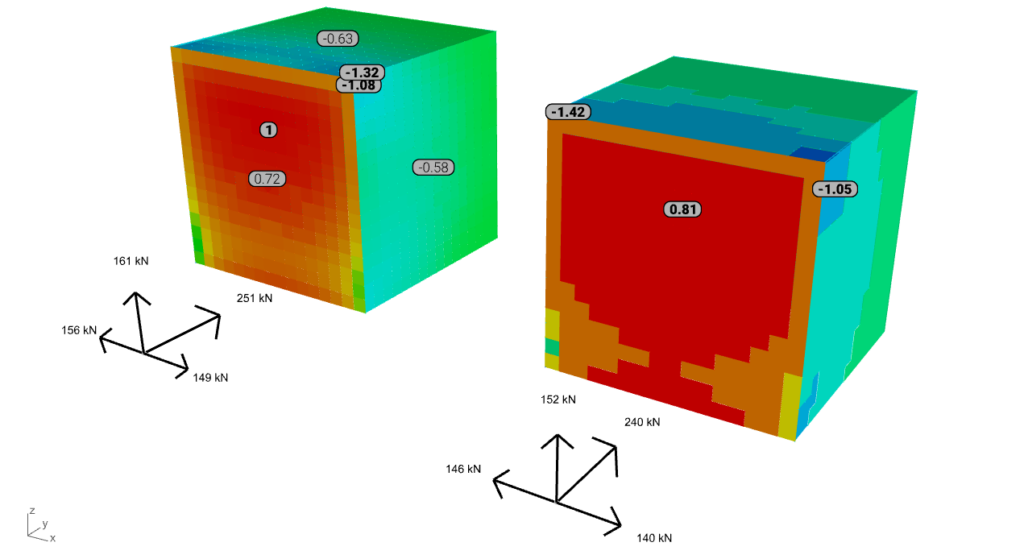
Bár az alapos, kétszeresen ellenőrzött validálás a szélcsatorna-kísérletek limitált háttérinformációi miatt kihívást jelenthet, a jelenlegi validálásaink már rávilágítottak arra, hogy a hálósűrűség és a turbulenciamodellek megfelelő kiválasztása kulcsfontosságú tényezők, amelyek jelentősen befolyásolják a nyomáseloszlást. A pontosság és a számítási hatékonyság közötti optimális egyensúly megtalálása továbbra is a béta tesztelési időszak kihívása marad. Éppen ezért a következő cikkekben tervezzük a validációinkat kiterjeszteni nagyobb léptékű, tipikus geometriájú modellekre. Célunk, hogy megkönnyítsük a használt szabványokkal való érdemleges összehasonlításokat, és átfogó iránymutatásokat nyújtsunk a szimulációs eredményekből feldolgozott hatékony szélteher-generáláshoz.
Referenciák:
[1] Dataprocessing and velocity-based validation on a simple block – https://consteelsoftware.com/ro/knowledgebase/dataprocessing-and-velocity-based-validation-on-a-simple-block/
[2] Baines, W. D., 1963. Effects of velocity distributions on wind loads and flow patterns on buildings, Proceedings, International Conference on Wind Effects on Buildings and Structures, Teddington, U.K., 26–28 June, 198–225
[3] Aerodynamic database for low-rise buildings – https://wind.arch.t-kougei.ac.jp/system/eng/contents/code/tpu
[4] EN 1991-1-4: Eurocode 1: Actions on structures – Part 1-4: General actions – Wind actions
A szél-szimulációval foglalkozó sorozatunk második cikkében a szerkezeti mérnöki tervezéshez kapcsolódó szél-szimuláció két
kritikus témáját tárgyaljuk. Az első az adatfeldolgozás, amely a numerikus áramlástanon alapú szélterhelés-generálás legfontosabb lépéseit foglalja magában, mint például a háló létrehozása, a szimuláció végrehajtása és az elsődleges eredmények kinyerése. A második téma egy előzetes, sebességalapú ellenőrzési példa, amely szélesebb körű magyarázatot nyújt a szimulációs paraméterek hatásairól, hogy biztosítsuk az eredmények pontosságát és hasznosságát a gyakorlati tervezési alkalmazásokban.
Az előző cikkben [1] áttekintettük a szél-szimuláció előfeldolgozási lépéseit, beleértve a geometria beállítását szimulációs felületek és peremfeltételek (szélhatások és irányok) segítségével. Ezek a paraméterek nagyrészt összhangban voltak a szabványok alaplogikájával, így értelmezésük viszonylag egyszerű. Azonban a folytatás érdekében elengedhetetlen, hogy röviden bevezessük a szimulációhoz kapcsolódó paramétereket is, amelyek két kategóriára oszlanak.
Az alapbeállítások közé tartozik a „hálóméret a szerkezeten” és a „hálófinomítási tényező”. Az első a szerkezeten generált hálók, a mechanikai célú véges elem háló és a numerikus áramlástanból származó véges térfogat háló átlagos élhosszát jelenti, amelyeket az előző cikkben ismertettünk. A finomítási tényezőt pedig arra használják, hogy növeljék a véges térfogat cellák élhosszát a szimulációs tartomány határain, mivel ezeket elég távolinak tekintjük az épülettől. Ezért nem szükséges olyan sűrűn számítani a mezőértékeket, mint az épület körül, ahol a „hálóméret a szerkezeten” paraméter alapján történik a sűrűbb hálóképzés, ami gyorsabb szimulációkat eredményez.
Megjegyzés: A nagyobb hálóméret a szerkezeten és a magasabb finomítási tényező durvább hálót eredményez, ami gyorsabb szimulációt, de kevésbé pontos eredményeket ad!
A haladó beállítások egy sor olyan paramétert tartalmaznak, amelyek a szimuláció hátterét szabályozzák. Az alapértelmezett értékek általában megfelelő eredményekhez vezetnek, de ennek a cikknek a célja, hogy betekintést nyújtson ezen paraméterek hatásába.
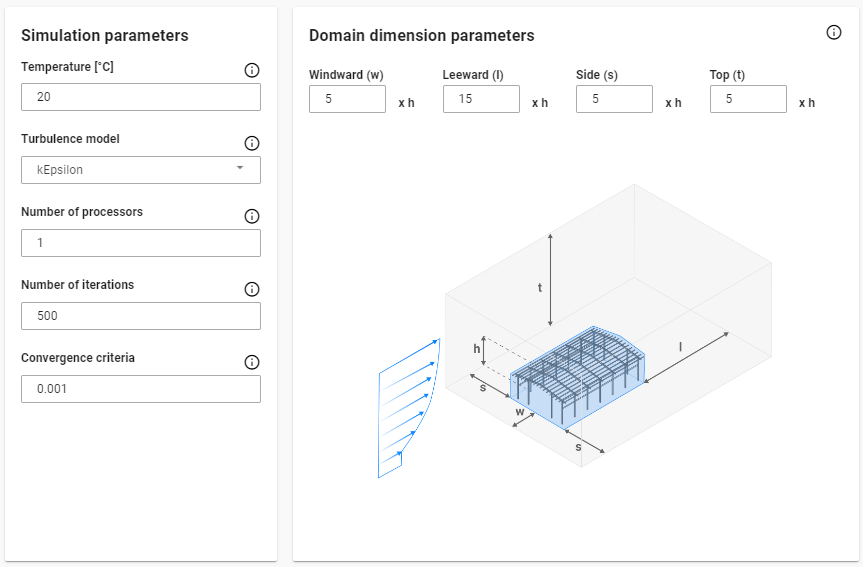
A megbízható validáció érdekében egy szélcsatorna tesztet reprodukáltunk, az Architectural Institute of Japan (AIJ) Benchmarkjai [2] által biztosított kísérleti adatok és számítási paraméterek felhasználásával. A kísérletet a Shimizu Corporation Műszaki Kutatóintézetének kis keringtetésű szélcsatornájában hajtották végre. A tesztmodell egy akril téglatestből állt, amelynek magassága 160 mm, szélessége pedig 80 mm volt. A beáramló szél sebességét 6,75 m/s-ra állították be, a mért turbulencia-intenzitás pedig körülbelül 0,5% volt.
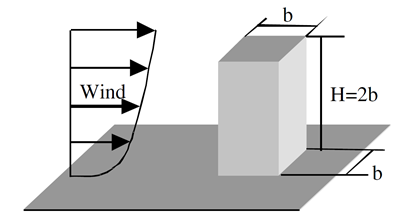
épületforma esettanulmányának beállításai
Megjegyzés: Ezeket a validációkat a Grasshopper környezetben a fejlesztési verziójában végeztük el az eszközünknek. A Consteel-ben az eszköz a szélterhelések generálására összpontosít, így a nyomásértékek kinyerésére is felhasználható.
A teljes elemzési folyamat során számos kulcsfontosságú szempontot figyelembe vettek az esettanulmány során. Mivel a modell a gyakorlatban előforduló egyik legegyszerűbb geometriát képviseli, és a szerkezeti viselkedése az irányelvek keretein belül könnyen értelmezhető, ez az eset több célra is szolgált. Elsősorban arra használták, hogy hangsúlyozza a hálófüggetlenségi tesztek elvégzésének fontosságát a tényleges szimuláció előtt. Az alábbi táblázatban látható, hogy még egy egyszerű geometria esetén is a hálósűrűség hatása jelentősnek bizonyult – nemcsak az eredmények pontossága, hanem a teljesítmény szempontjából is. A további vizsgálatokhoz a „2000-4” hálókonfigurációt választották, ahol az eredmények konvergenciája nyilvánvalóvá vált.
| Mesh size on structure [m] | 8000 | 4000 | 2000 | 1000 |
| Mesh refinement factor | 2 | 3 | 4 | 5 |
| Meshing runtime [s] | 18.3 | 65.3 | 61.2 | 108.9 |
| Cell number [-] | 136432 | 150881 | 264786 | 495694 |
| Simulation runtime [s] | 65.3 | 57.9 | 151.1 | 343.4 |
| Iterations [-] | 264 | 182 | 260 | 314 |
| Fx+ [kN] | 197 | 203.0 | 205.6 | 203.5 |
| Fy+ [kN] | 94.4 | 94.5 | 89.9 | 89.7 |
| Fy- [kN] | 94.5 | 94.4 | 89.8 | 89.8 |
| Fz+ [kN] | 53.6 | 52.4 | 47.7 | 48.2 |
A következő szempont a hálófinomítás jelentőségének hangsúlyozása volt, különösen az élek mentén. Például a finomabb hálófelbontások nagyobb szívóértékeket rögzítenek az oldalfalakon, bár kisebb lokalizált területeken. Ennek következtében elengedhetetlen a globális reakciók figyelemmel kísérése az adott hálókonfiguráció által befolyásolt nyomások hatására, ahogy azt a fenti táblázat is bemutatja.
A kezdeti kalibrálási teszteket követően öt különböző turbulencia modellt (k – ε, k – ω, k – ω SST, RNG k – ε, Realizable k – ε) hasonlítottak össze a saját sebességi mezőik alapján.
Ezeket az eseteket egy időben hajtották végre, hogy felmérjék a teljes processzorhasználat hatását. A hálózási folyamat során majdnem minden esetben ugyanazt a hálót alkalmazták; azonban a futási idő körülbelül 250 másodpercre nőtt, ami négyszer hosszabb, mint amikor az eseteket külön futtatták. Ez világosan jelzi, hogy az előzőleg jelentett futási időket jelentősen befolyásolta a párhuzamos folyamatok egyidejű végrehajtása.
Megjegyzés: Lehetséges egyetlen szimulációs eset párhuzamos futtatása is, amely magában foglalja a számítási tartomány lebontását, majd annak újbóli rekonstrukcióját. Ez a lebontási folyamat azonban szintén számítási erőforrásokat igényel, ami azt jelenti, hogy a párhuzamos szimulációk futtatása nem mindig eredményez gyorsabb végrehajtási időket.
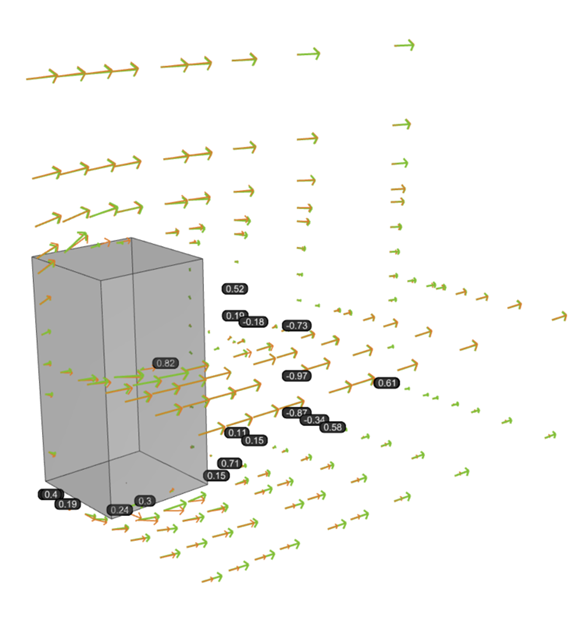
Az egyes esetekhez használt elsődleges metrikus az átlagos irányeltérés volt, amely a szimulációból származó sebességvektorok és a referencia kísérleti sebességvektorok közötti eltérést méri, ahol a 0 párhuzamos vektorokat, míg az 1 merőleges vektorokat jelöl. Az összes szcenárió során hasonló viselkedést figyeltek meg az épület mögötti áramlási területen, amely hangsúlyozza a RANS-típusú turbulenciamodellek egyik fő korlátját. Ezek a modellek jellemzően csak egyetlen domináns örvényt képesek rögzíteni az áramlás leválásakor, ami a legnagyobb eltérésekhez vezet az épület mögött, valamint a talaj közelében.
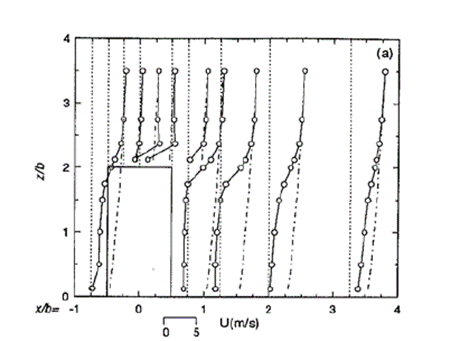
cikkéből származó eredeti adatok
A releváns és átlátható validációk biztosítása érdekében az eredeti AIJ benchmark eredményeket összehasonlították a különböző turbulenciamodellek alkalmazásával nyert eredményekkel hasonló módon. A számítási tartományon belül az épülethez közeli pontok halmazát figyeltük meg.
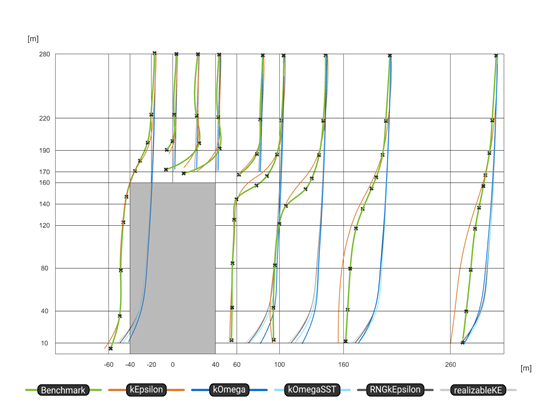
Összegzésül elmondható, hogy bár ezek a sebességi mezőkön alapuló validációk korlátozott közvetlen relevanciával bírnak a szerkezeti mérnöki szempontból, a széláramlás viselkedésének megértése az épületek körül és a szimulációk megfelelő kalibrálása továbbra is kulcsfontosságú. Nyilvánvaló, hogy még a legegyszerűbb geometriák esetén is a szimulációs eredmények rendkívül érzékenyek a paraméterváltozásokra, ami hangsúlyozza az iteratív megközelítés szükségességét a hálófüggetlenség és az eredmények konvergenciájának biztosítása érdekében.
A vizsgálat során a cél egy általános iránymutatás kidolgozása volt a jobb kezdőértékek érdekében. Ennek megfelelően a javasolt hálóméret a szerkezeten e/12 és e/20 között legyen, ahol „e” a szerkezet keresztirányú szélessége és kétszeres magassága közötti minimum értéket jelenti, ahogy azt az EC 1991-1-4 [3] definiálja. Ezt kiindulási pontként használva ajánlott egy iteratív szimulációs folyamatot alkalmazni, amelynek finomítási tényezője 5 és 0 között mozog, miközben folyamatosan figyelemmel kísérjük a nyomás eredmények konvergenciáját. Ez az iteratív módszer képezi az alapját a terhelésgenerálási eljárásnak a posztfeldolgozási fázis során, amelyről további részletek lesznek olvashatók a következő tudásbázis anyagokban.
Irodalomjegyzék:
[1] Szél-szimuláció előfeldolgozása szerkezeti mérnöki célokra
[2] CFD előrejelzések útmutatója a városi szélkörnyezethez – Japán Építészeti Intézet
[3] EN 1991-1-4: Eurocode 1: Terhelések szerkezetekre – 1-4. rész: Általános terhelések – Szélhatások
A szélszimulációs és tehergeneráló eszközünknek közzétételére készülve, fedezzük fel azokat az elméleti és technológiai háttéreket, amelyek egyedivé teszik. A fejlesztési folyamat során jelentős eltéréseket azonosítottunk a numerikus áramlástan és a szerkezeti mechanika világa között, emiatt jelentős szaktudásbeli felzárkózásra van szükség. Elkötelezettek vagyunk amellett, hogy felelősségteljes fejlesztői-felhasználói közösséget támogassunk, ezért úgy döntöttünk, hogy az elkövetkező hónapokban több tudásbázis anyagot publikálunk, amelyek elmagyarázzák azokat a kulcsfontosságú jellemzőket, amelyek elsősorban a Consteel tervezési munkafolyamat mögött működnek. Az első lépés az eszköz előfeltételeinek megértése és annak meghatározása, hogyan törekszünk a véges elemes, szabvány alapú tartószerkezet mérnöki megközelítés összehangolására a numerikus áramlástanban véges térfogatos módszerekkel. Röviden, ezt nevezzük előfeldolgozásnak. Nézzük meg, mit is jelent ez pontosan.
A tartószerkezeti mérnöki gyakorlatban a szél által okozott terhelések értékelése általában olyan szabványos eljárásokkal történik, amelyek különböző módokon egyszerűsítik a tényleges jelenséget. Azonban amikor fejlettebb módszereket, például numerikus áramlástant alkalmazunk, ezek a szabványok elkerülhetetlenül mérceként szolgálnak, alapot adva a szimuláció által generált nyomási eredmények összehasonlításához.
A teljes fejlesztési folyamat a szabványos eljárásokkal meghatározott szélprofilokra összpontosított . Az első megvalósítás az Eurocode 1-4 alapján készült, amely egy sor paraméterre épül, hasonlóan a Consteel-on belüli meteorológiai hatások meghatározásához.

A torlónyomási paraméterek magukban foglalják a szélsebességet alapértékét (vb), amelyet a különböző országok földrajzi zónái alapján lehet kiválasztani, valamint a beépítettségi osztályt. A beépítettségi osztály, amelyet a kiválasztott nemzeti melléklet ad meg, különböző további értékeket határoz meg, mint az érdességi hossz (z0), a legkisebb magasság (zmin) és a beépítettségi tényező (kr). A beépítettségi tényező lehet rögzített érték, ahogy azt több nemzeti melléklet is meghatározza, vagy lehet kiszámítandó egy javasolt képlet alapján, amely az érdességi hosszt és a legkisebb magasságot veszi figyelembe. Ezenkívül a kiválasztott nemzeti melléklet alapvető értékeket biztosít a levegő sűrűségre (ρ), a domborzati tényezőre (co(z)) és az örvénylési (turbulencia) tényezőre (kI) is.
A belső nyomási paraméterek olyan együtthatókat tartalmaznak, amelyek módosítják a szélterheket egy adott szélirány esetén, így véve figyelmbe a a belső nyomások hatásait, az Eurocode alapján.
Megjegyzés: A fejlesztés jelenlegi szakaszában erősen ajánlott az eszközt kizárólag zárt, „légmentes” épületek külső nyomásának meghatározására használni.
A geometriai paraméterek közé tartozik az alap szélirány meghatározása a globális koordinátarendszer szerint (θ = 0°), a talajszint (Z), valamint egyéb méretparaméterek. Ezek a paraméterek felhasználhatók zónázott terhelések létrehozására, lehetővé téve olyan terhelési felületek kialakítását, mint amilyeneket az Eurocode meghatároz.
Végül a szél szimulációs felületek a vizsgált épületet körülvevő felületek, amelyek teher átadó felületként szolgálnak a későbbi statikai számításokhoz.
Megjegyzés: Jelenleg a szimulációk csak felületeken végezhetők el, és nem alkalmazhatók rúd elemekre.
Miután az összes szükséges, a szabványok alapvető logikájával összhangban lévő paraméter megadásra került, a tényleges előfeldolgozás egy külön dialógból indítható el. Ez a kezelőfelület további áramlástannal kapcsolatos bemeneteket igényel, amelyekről a következő tudásbázis anyagokban lesz szó.
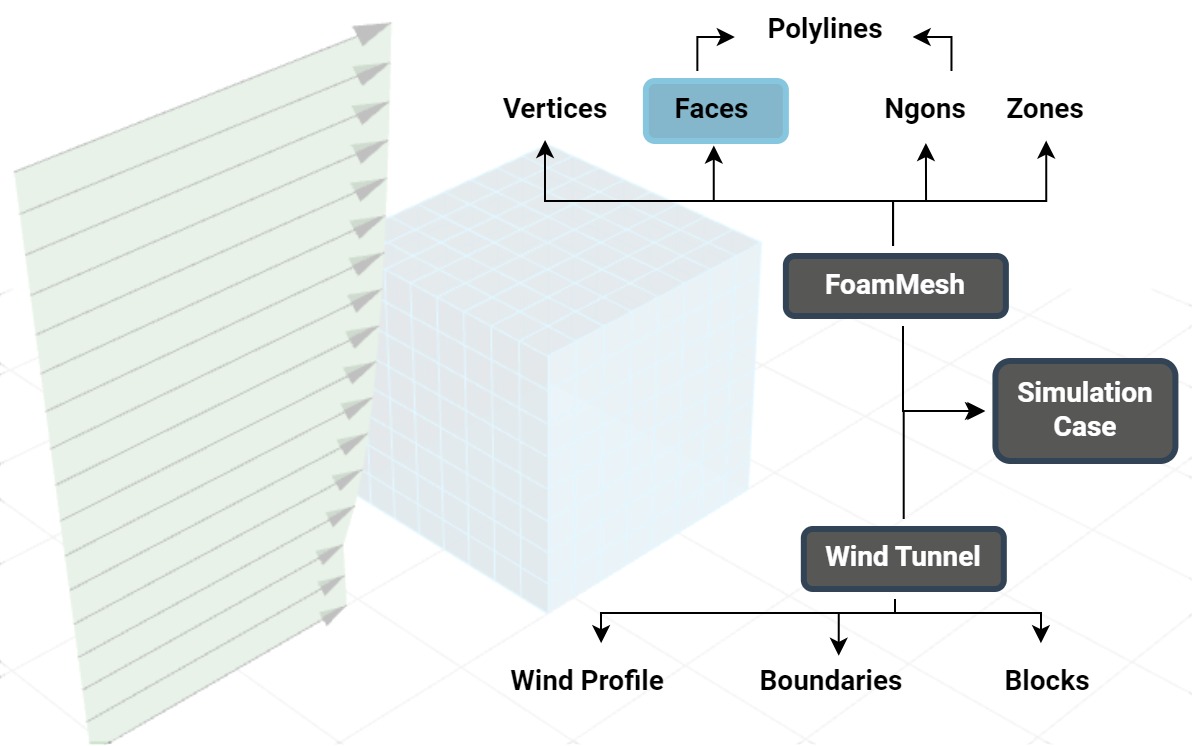
Az előfeldolgozás egy fő fázisként is értelmezhető, két fő feladattal, amelyek a korábban összegyűjtött paraméterek alapján hajtódnak végre. Az első feladat az, hogy a bemeneti geometriát egy speciálisan kifejlesztett hálóformátumba (FoamMesh) alakítsa át. Ez a formátum egy hagyományos véges elemes hálóra hasonlít, háromszög vagy négyszögletű sík felületekkel és csúcsokkal rendelkezik, és képes a szimulációs eredmények tárolására. Ezenkívül a FoamMesh képes értelmezni az OPENFOAM® által generált, sokszögletű felületeket (’Ngon’), amelyek gyakran nem sík felületekből állnak. A felületek eredményeik alapján zónákat is alkothatnak.
Megjegyzés: A szimulációhoz használt véges elemes háló eltér attól a hálótól, amelyet a statikai számítások során a teherelosztásra szolgál. A szimuláció specifikus háló belső hálópontjait a felületi kontúr iteratív eltolásával kapjuk, és elsősorban négyszögletű felületek létrehozására törekedve. Ezek a négyszögletű felületek előnyösek a zónázott terhelések létrehozásához az utófeldolgozási fázisban.
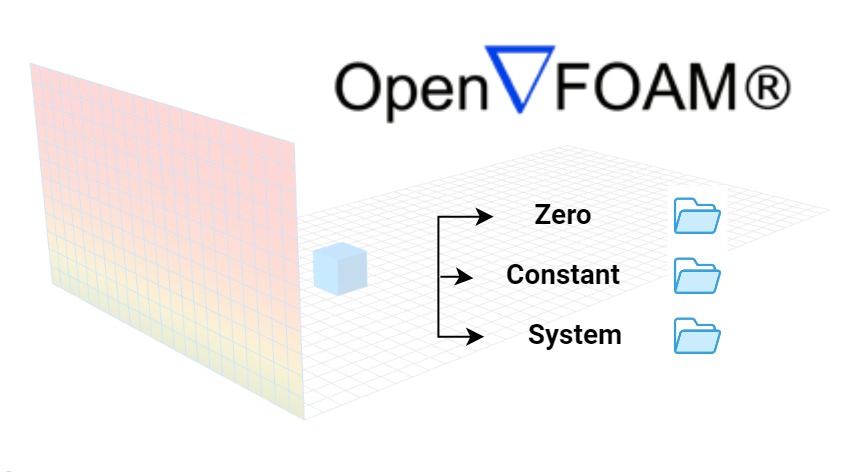
A másik fő feladat egy virtuális szélcsatorna létrehozása, amely a paramétereknek megfelelő szélprofilból, valamint a szimuláció során használt, határokkal és belső cellákal (véges térfogatok) definiált zárt tartományból áll. Ez alapján lehetséges a szimulációs esetek tartalmának létrehozása az OPENFOAM® speciális hierarchiájának megfelelően. A széláramlási paraméterek a „zero” mappában tárolódnak, a háló generálása a „constant” és „system” mappákban, míg a megoldási és eredménylekérdezési paraméterek a „system” mappában kerülnek.
Megjegyzés: Minden szélirányhoz külön szimulációs eset tartozik, amely saját, független véges térfogat háló alapú szélcsatornával rendelkezik. Az épület véges elemes hálója azonban azonos marad, függetlenül az iránytól.
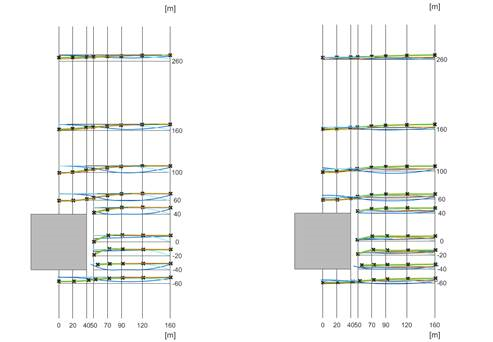
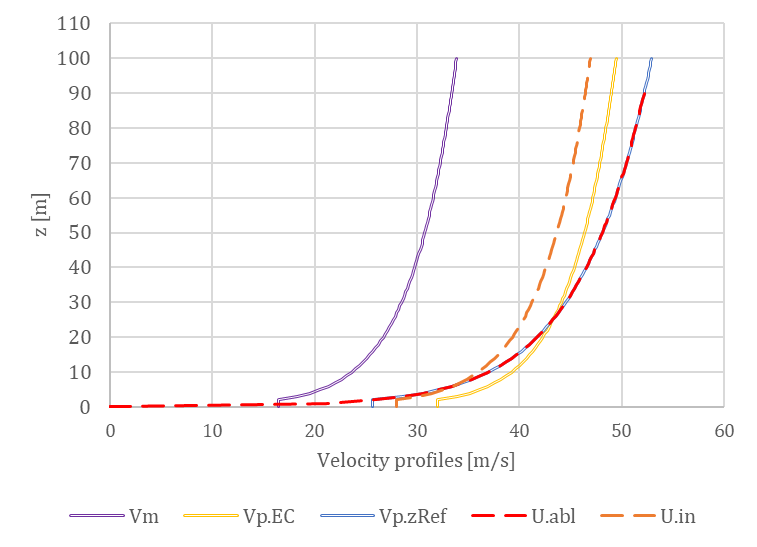
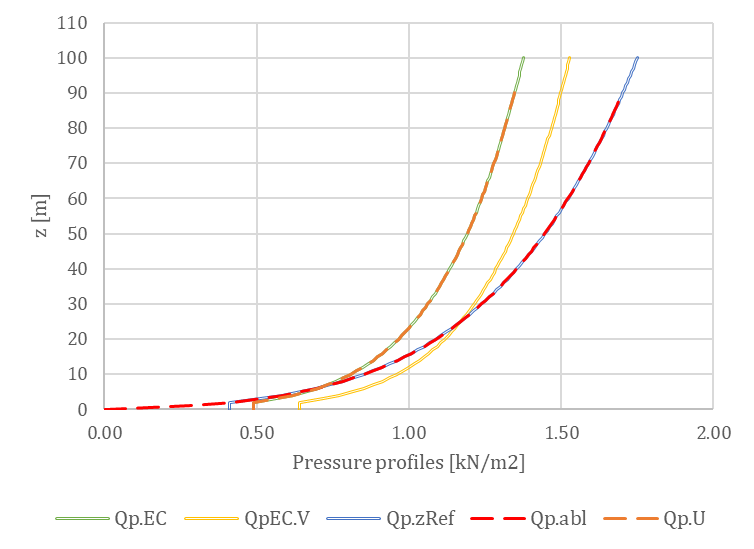
A szélprofil tekintetében az egyértelmű cél az, hogy olyan szélsebesség-profilt vezessünk be, amely a szabvány által meghatározott torlónyomás profilt képez. Azonban ennek a profilnak a definiálása nem egyértelmű feladat. Az alábbi ábrák különböző megközelítéseket szemléltetnek, a QpEC függvény pedig az Eurocode által meghatározott általános „cél” profilt mutatja.
Mivel az Eurocode általában elhanyagolja a turbulencia intenzitás másodrendű tagját (csak az 1 + 7Iv(z) tagot veszi figyelembe) a QpEC kiszámításánál, jelentős különbség adódik, ha a torló sebességprofilt használjuk a sebességnyomás (QpEC.V) kiszámításához (az 1 + 3.5Iv(z) tagokat alkalmazva a turbulencia intenzitásra). Ennek következtében a VpEC közvetlen implementálása az OPENFOAM®-ban nem célszerű.
A szabványokon kívül az OPENFOAM® egy alapértelmezett megközelítést is kínál a logaritmikus atmoszférikus határrétegekhez (Uabl), amely a súrlódási sebességből (U*) indul ki, ami egy referencia magasságon számolódik. Az így kapott Qp.abl szintén jelentős eltérésekhez vezethet, mivel hiányzik a zmin alatti állandó szakasz. Ettől eltekintve egyébként ez a profil hasonló a szabványos Vp(zRef) profilhoz, amely a magasság mentén egyetlen konkrét turbulencia-intenzitás szerint értékelődik, ami a referencia magasságon (Iv(zref)) van számolva.
Az OPENFOAM® által alkalmazott logaritmikus profil az atmoszférikus határréteg megközelítéssel a következőképpen értékelhető:
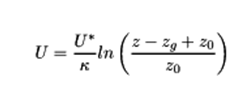
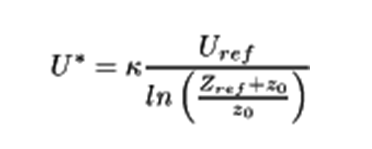
Ezért szükséges volt egy egyedi megoldás kifejlesztése az OPENFOAM®-on belül az Uin bemeneti sebességprofil meghatározásához, amely az elvárt QpEC értéket produkálja. Ehhez a következő képlet van alkalmazva:
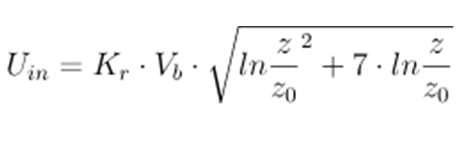
Egy bemeneti szélprofil esetén, amely a k-ε turbulencia modellt használja, a k (turbulens kinetikus energia) és ε (turbulencia disszipációs ráta) mezők kezdeti értékeinek beállítása is szükséges. Ehhez különböző megközelítések léteznek. Az OPENFOAM® alapértelmezett atmoszférikus határrétege automatikusan konstans értéket számít a magasság mentén, a következőképpen:
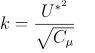
Azonban a bemeneti turbulens kinetikus energiát (k) általában a bemeneti referenciasebesség és a turbulenciaintenzitás alapján számítják, amelyet az Eurocode a terepparaméterek alapján határoz meg, ahogyan azt korábban bemutattuk. Ez alapján a turbulens kinetikus energia számítható:
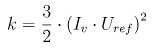
Hasonlóképpen, a bemeneti ε (turbulencia disszipációs ráta) értékének meghatározására az OpenFOAM alapértelmezett automatikus módszert használ, amely a súrlódási sebességen alapul. Ez az alábbi képlettel számítható:
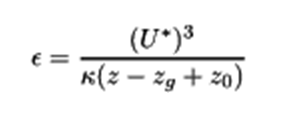
Ezen kívül van egy számítható megközelítés, amely az Eurocode-os eljárás szerint értékelhető örvénylési hossz alapján történik, a következőképpen:
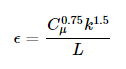
Ezek a megközelítések összehasonlításra kerültek mind a középsebesség, mind a csúcssebesség profilok esetében, ahogyan az alábbi ábrán is látható. A torlónyomások egy egyszerű 8 m x 8 m x 8 m kocka széltámadta falán számított értékeknek felelnek meg. A profilok elnevezési konvenciói a következőképpen van: bemeneti sebesség profil (átlag – m vagy csúcs – p) – bemeneti turbulens kinetikus energia ( automatikus – a vagy számított – c) – bemeneti turbulencia disszipációs ráta (automatikus – a vagy számított – c).
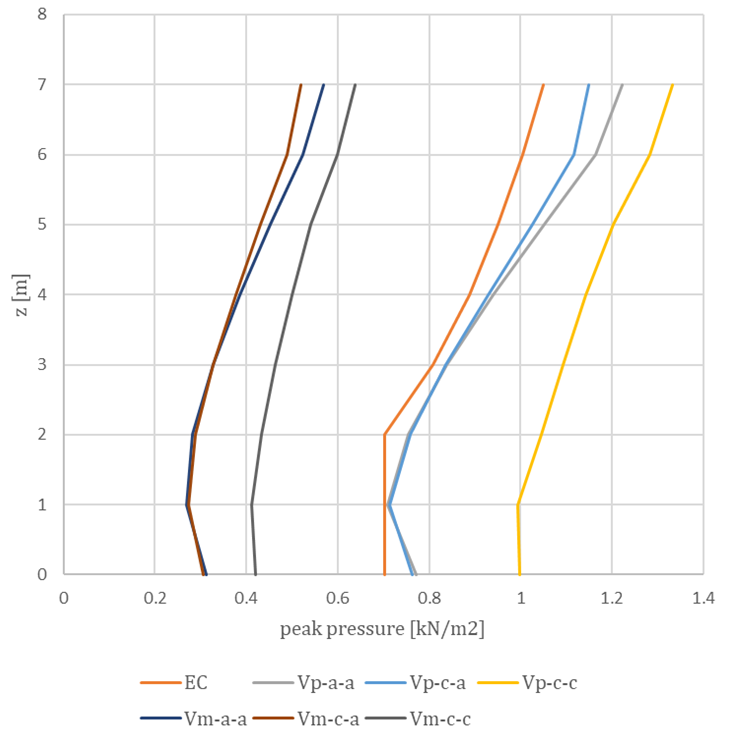
Ezek alapján tehát a U.in sebességprofil került kiválasztásra, mind a bemeneti turbulens kinetikus energia (k), mind a bemeneti turbulencia disszipációs ráta (ε) pedig az automatikusan módszer szerint értékelődik. A különböző turbulenciamodellek hatásait, valamint a különböző paraméterezés szerint generált véges térfogat hálók befolyását, ami már az adatfeldolgozási fázishoz tartozik, a következő tudásbázis anyagokban fogjuk tárgyalni. Validációs példákon keresztül fogjuk felfedezni ennek az újonnan kifejlesztett eszköznek a használatát, érdemes velünk tartani.
Program verzió: Consteel 17; Build 3303
Tervezés célja, tervezési szabvány kiválasztása
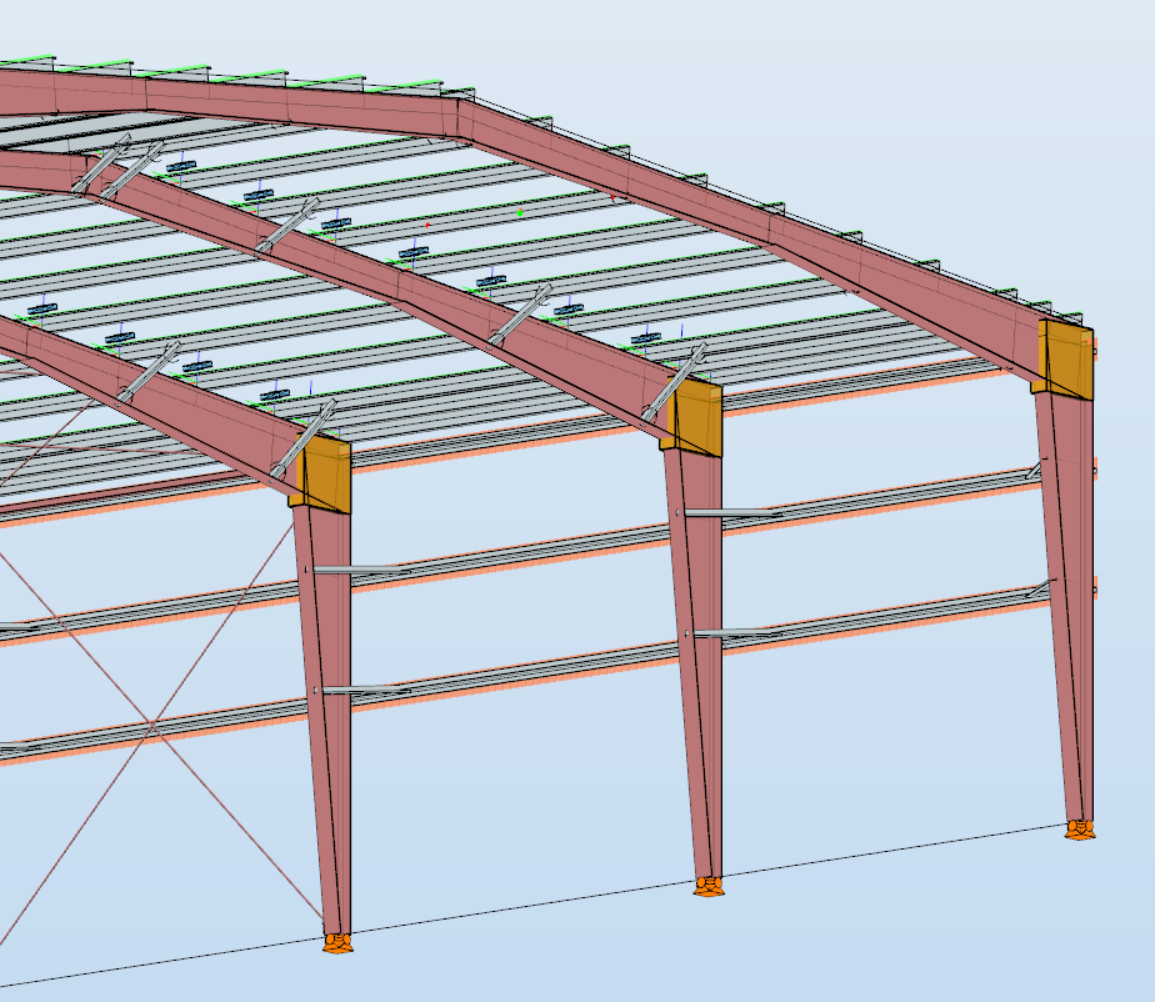
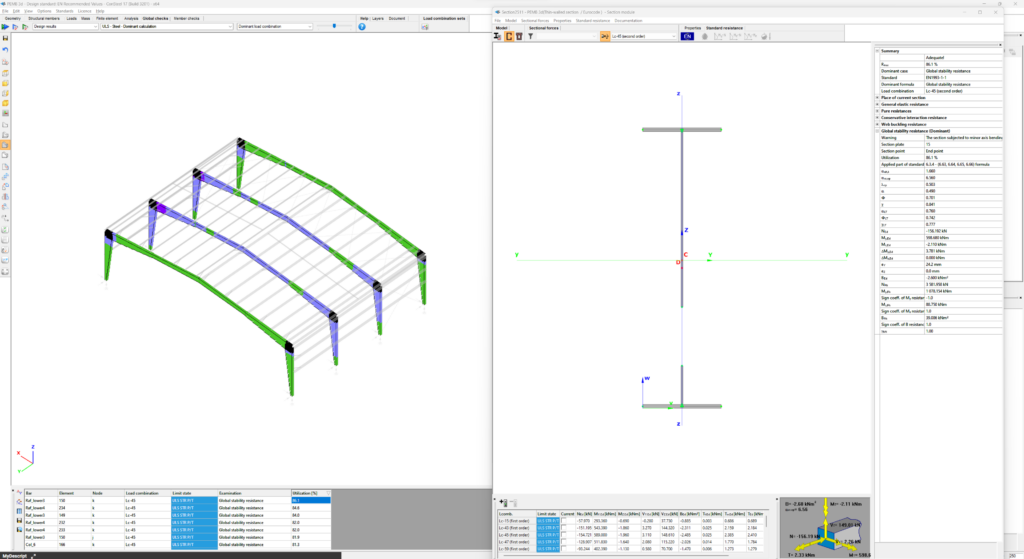
A jelen tervezési segédlet a kezdő ConSteel 17 felhasználó számára egy kéttámaszú rácsos tartó tervezését mutatja be, lépésről lépésre. Az építészeti koncepcionális tervből ismert a megtervezendő rácsos tartó geometriai kialakítása (1. ábra). A koncepció szerint a rácsos tartó övei HEA120 típusú melegen hengerelt szelvényből készülnek, míg a rácsrúdjai hidegen alakított SHS80x4 szelvényből. A jelen segédletnek a csomópontok tervezése nem része.
Ismert, hogy a szerkezettervezés mindig valamely szabvány, illetve annak változata szerint történik. A szabvány kiválasztása új modell létrehozásakor a Project centerben a Tervezési szabvány menüből választható, vagy később a Szabványok rendszerfül [S1] kiválasztó paneljében módosítható (2. ábra).
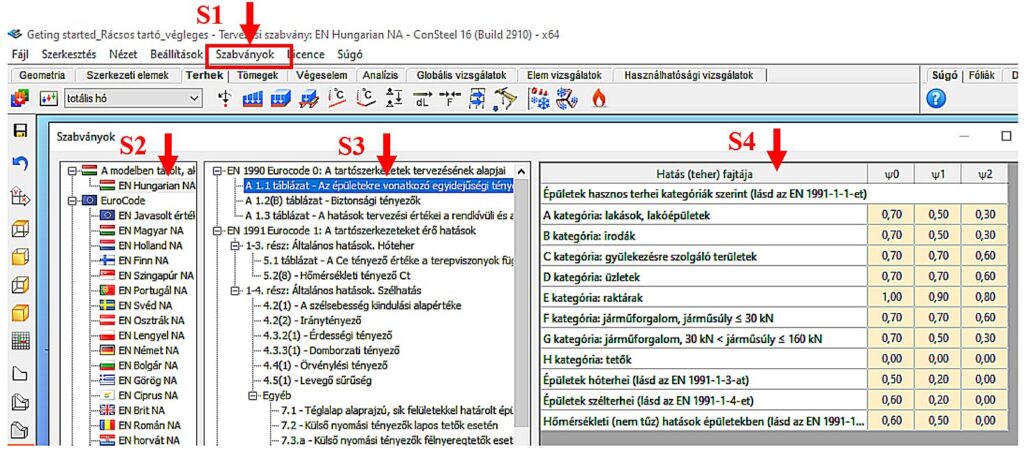
Az alkalmazni kívánt tervezési szabvány a panel bal oldali listájából választható ki. Jelen esetben az EN Hungarian NA opciót [S2] választjuk (MSz EN Magyar Nemzeti melléklet). A kiválasztott szabvány által alkalmazott paraméterek a középső tartalomjegyzék megfelelő sorának kiválasztásával érthető el, a jobb oldali táblázatban [S4]. A 2. ábrán az EC0 szabvány 1.1 táblázatának megfelelő egyidejűségi tényezők kerültek kiválasztásra, amely paramétereket a jobb oldali táblázat mutatja meg.
Szerkesztő raszter beállítása
Először állítsuk be a raszter méretét a szerkezet fesztávjának megfelelően. Ehhez alkalmazzuk a baloldalon található eszközcsoport megfelelő gombját [1], amelynek hatására megjelenik a Raszterháló és koordinátarendszer beállító panel (2. ábra).
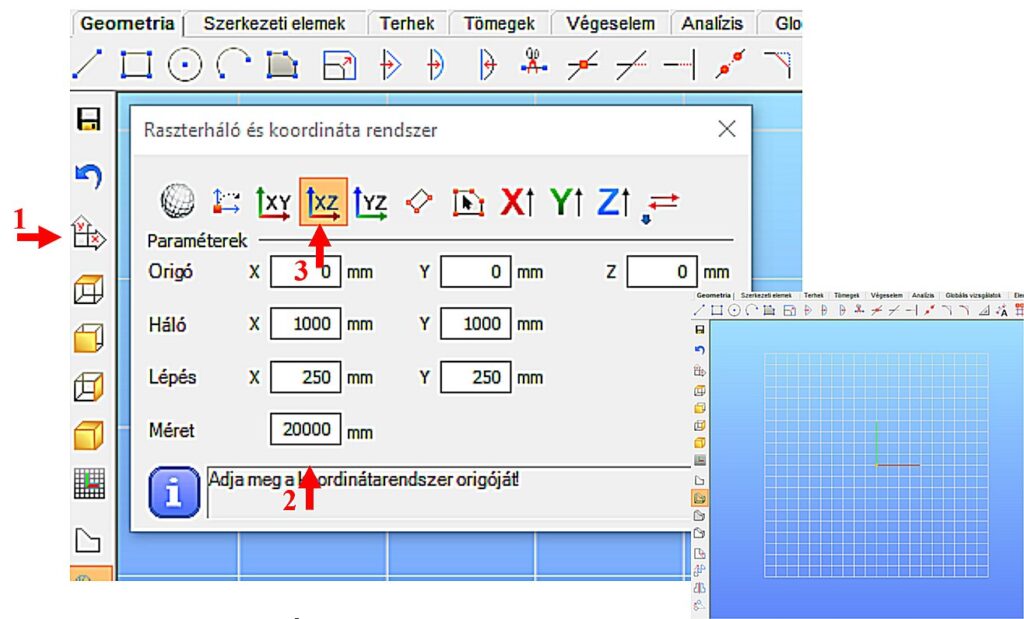
Például a 19.6m hosszú tartó esetén a Méret ablak tartalmát 20000 milliméterre állíthatjuk [2]. A beállítás aktualizálásához nyomjuk meg az Enter-t, vagy zárjuk be az ablakot. A fenti beállítás esetén a raszter X és Y irányban 20 méter széles lesz, a raszter vonalak sűrűsége 1000 mm, a lépésközök 250 mm. A rácsos tartó modellt célszerű az X-Z globális koordináta síkban felvenni, tehát a szerkesztő rasztert el kell fordítanunk az X-Z síkba. Ehhez válasszuk XZ sík opciót [3].
gateDid you know that you can use Consteel to design a pre-engineered Metal Building with all its unique characteristics, including web-tapered welded members, the interaction of primary and secondary structural elements, flange braces, shear and rotational stabilization effect provided by wall and roof sheeting?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free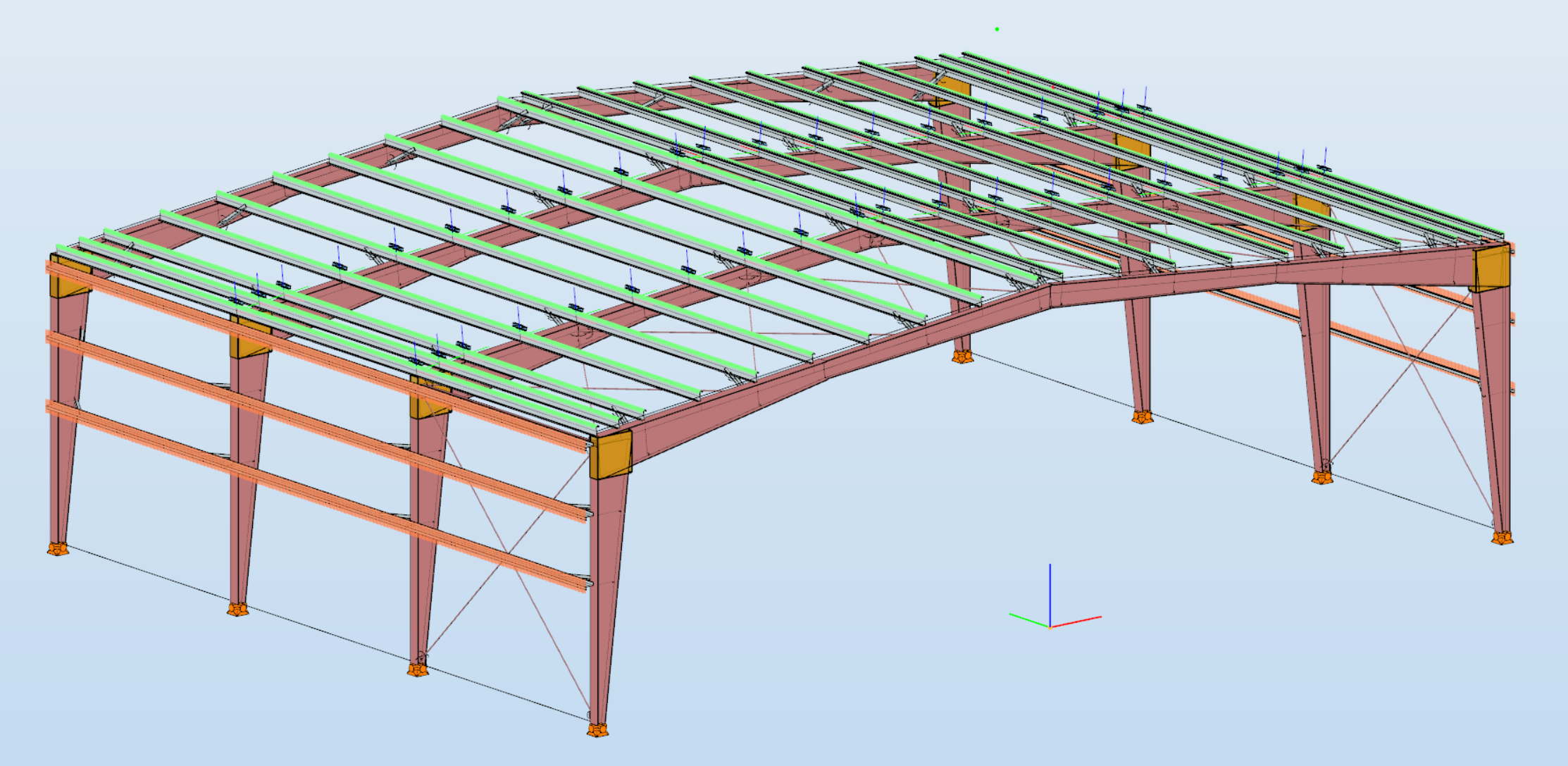
Ez a rövid áttekintés mélyebben ás a Consteel megoldásába, egy alternatív szemléletet nyújtva az effektív keresztmetszeti tulajdonságok kiszámításához, és formálva a hagyományos megközelítéseket a szerkezeti elemzés és tervezés területén.
Határozzuk meg a 384-4 gerinclemezű és 300-8 övlemezű kétszersen szimmetrikus hegesztett I keresztmetszet szilárdsági kihasználtságát, amennyiben a keresztmetszet igénybevételei az NEd=500kN nyomóerő és az My,Ed=100kNm hajlító nyomaték. A keresztmetszet anyaga S235 minőségű.
Keresztmetszeti jellemzők számítása
Először vegyük fel a keresztmetszet adatait (szimmetrikus hegesztett I szelvény), amely alapján a Consteel software generálja az EPS (és GSS) (Online Kézikönyv/10.1.1 EPS (vékonyfalú szelvény) modell) keresztmetszeti modellt (1. ábra):
Amennyiben a keresztmetszet 4. osztályba tartozik, az effektív keresztmetszeti modellt a feltételezett normálfeszültségi eloszlás határozza meg. Az EC3-1-1 szerint a 4. keresztmetszeti osztályú szelvény EPS keresztmetszeti modellje kétféleképpen határozható meg:
- A módszer: tiszta igénybevételi állapotok alapján,
- B módszer: összetett igénybevételi állapot alapján.
Először az A módszerrel számoljuk ki a keresztmetszeti tulajdonságokat, majd a B módszerrel.
Keresztmetszeti jellemzők az A módszer alapján
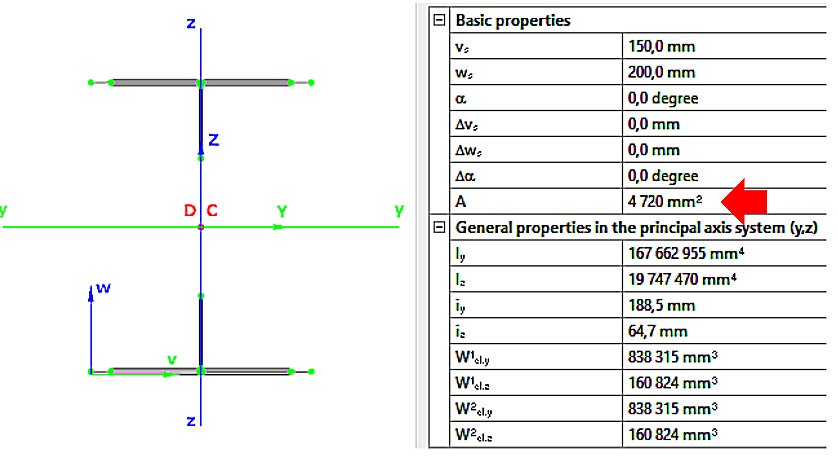
- NEd nyomóerő esetén (2. ábra):
- Aeff=4720mm2
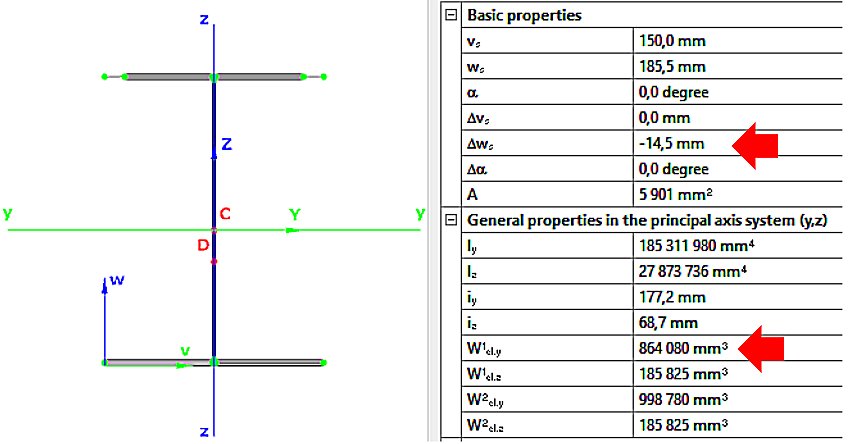
- My,Ed hajlító nyomaték esetén (3. ábra):
Weff,y,min=864080mm3
ez=14.5mm
Keresztmetszeti jellemzők a B módszer alapján
GATEThe latest version, Consteel 17 is officially out! In 2023, our main focus for Consteel development is improving usability. New features prioritize efficient model manipulation, easy modification, and clear information presentation across Consteel, Descript, and our cloud-based platform, Steelspace. In this comprehensive video, we walk you through a step-by-step workflow guide, demonstrating how to leverage Consteel 17 to its full potential.
If you would like to delve deeper into the new features, check out our detailed blog post for an in-depth exploration of Consteel 17’s capabilities.
A Consteelben a 3. és 4. osztályú szelvények keresztmetszeti interakciós ellenállása az EN 1993-1-1 6.2 képlet módosított változatával kerül kiszámításra, az öblösödés és a komponens ellenállások előjelhelyes figyelembevételével. Lássuk, hogyan…
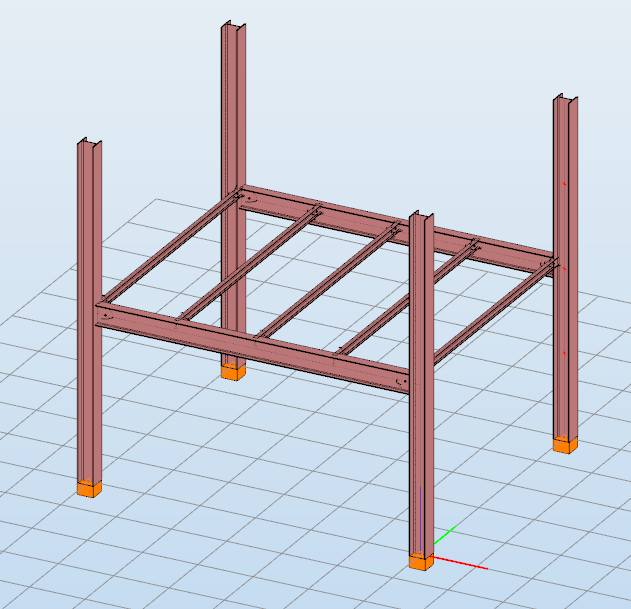
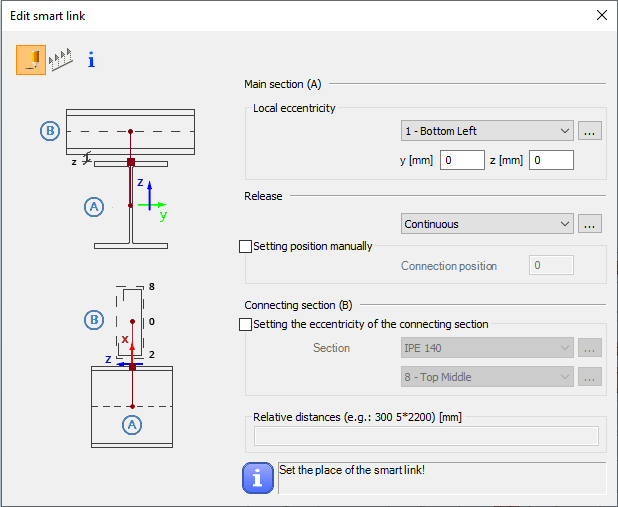
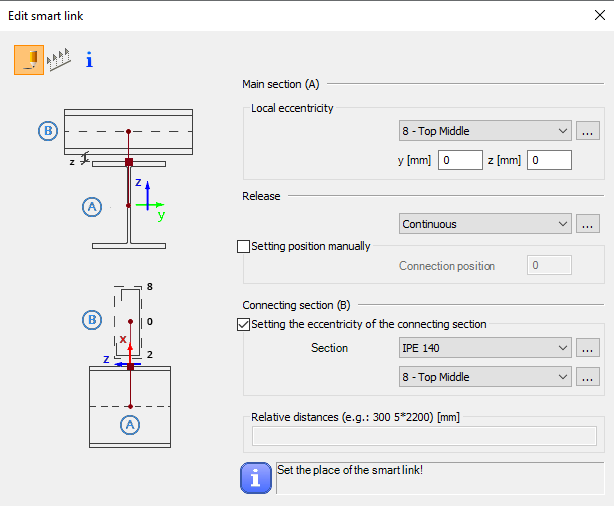
GATEDid you know that you could use Consteel to build 3D models with smart link elements which automatically adapt the model when profiles are changed?
Download the example model and try it!
Download modelIf you haven’t tried Consteel yet, request a trial for free!
Try Consteel for free