Vasbeton oszlopok tervezése - a Névleges Görbületi Módszer alkalmazása

Bevezetés

A vasbeton oszlopok az építőipar alapvető szerkezeti elemei. Előfordulnak például keretvázas épületekben, csarnokokban, családi házakban, de hidaknál is. Alkalmazzák mind monolit, mind előregyártott változatban is.

A tervező célja biztonságos és gazdaságos szerkezetek tervezése. A technológia fejlődésével építőanyagaink is változnak, egyre jobb minőségű betonokat lehet előállítani kedvező költségek mellett. Ennek következtében előnyössé válhat kisebb keresztmetszetű oszlopok alkalmazása.

Ahogy az oszlopok karcsúbbak lesznek, előtérbe kerülnek a stabilitási kérdések és a másodrendű igénybevételek számítása. A ConSteel végeselemes program acélszerkezetekre van specializálódva, ebből kifolyólag pedig gyors és jól automatizált megoldásai vannak stabilitási problémákra.

Kihasználva a szoftverben meglévő lehetőségeket, a ConSteel szoftver 16-os verziójában elérhetővé vált a vasbeton oszlopok tervezésére egy újfajta, ConSteel által továbbfejlesztett módszer alkalmazása. Ez az Eurocode 5.8.8 [1] -ben leírt Névleges görbület módszeren alapszik.

A Névleges görbület módszere alkalmazásához sok információt kell megadni, különféle anyagi-és geometriai paramétereket. A dokumentum célja bemutatni, hogy a ConSteel 16-ban kiterjesztett Névleges görbület módszer választ ad az összes tervezés közben felmerülő kérdésre, és mentes az eredeti módszer több hiányosságától is.

Az Eurocode 2 áttekintése - vasbeton oszlopok tervezése

Ebben a fejezetben az Eurocode 2, Névleges görbület módszerén alapuló vasbeton oszlopok tervezését mutatjuk be nagyvonalakban, összpontosítva a hangsúlyosabb részekre.

Anyagi paraméterek

Parciális biztonsági tényezők:

• Beton rugalmassági modulusa
  𝛾_cE = 1.20
  
• Beton
  𝛾_c = 1.50
  
• Acélbetét
  𝛾_s = 1.15

A beton anyagi tulajdonságaival az Eurocode 1992-1-1 3.1. fejezete foglalkozik.

Rugalmassági modulus:

• Tervezési érték
  
  • 𝐸_cd = 𝐸_cm/γ_cE
    
  • A várható érték csökkentése γ_cE biztonsági tényezővel
    
  • Teherbírási vizsgálat esetén alkalmazandó
    
  • Abban az esetben, ha a kúszást nem kell figyelembe venni, vagy máshol vesszük figyelembe
    

Kúszás

A kúszási tényező számításáról az EN 1992-1-1 3.1.4 fejezet beszél. Itt különböző tényezők segítségével meg lehet határozni a kúszási tényező végértékét, betonszilárdság függvényében, diagramok segítségével. Az értékek meghatározhatóak az EN 1992-1-1 B Melléklete szerint is. A két számítás közel azonos eredményhez vezet.

Imperfekciók

Az imperfekciók figyelembevételét az Eurocode 1992-1-1 5.2-es fejezete taglalja. Az imperfekciók figyelembevételét alapvetően két részre bontja. Az egyik a globális ferdeség, ez látható a 1. ábra b) részén. A másik rész amikor a hálózati pontok nem mozdulnak el, de közte az elemek görbültek. Ez a kezdeti görbület (vagy más néven alakhiba), a 1. ábra c) része szemlélteti.

Ferdeség

A ferdeségből származó imperfekció hatását figyelembe lehet venni fiktív keresztirányú erők számításával. Ehhez az alkalmazott ferdeség értékét a következőképpen kell számolni:

• ferdeség alapértéke
  θ₀ = 1/200
  
• magasságtól függő csökkentő tényező
  α_h = 2/√𝐻
  
  ahol 𝐻 a magasság
  
• szerkezeti elemek számától függő csökkentő tényező
  α_m = √0.5(1 + 1/𝑚)
  
  𝑚: teljes hatás felvételében szerepet játszó függőleges szerkezeti elemek száma
  
• alkalmazott ferdeség
  θ_i = θ₀α_hα_m                   

Ezek után az 2. ábrán látható módon az  normálerőkből merevítetlen estben a fiktív keresztirányú erők számolhatóak: 𝐻_i = θ_i𝑁 módon..

Merevített esetben, például egy csuklós-csuklós oszlopnál a 𝐻_i  erőt nem a rúd tetőpontjába, hanem a rúd középpontjába kell definiálni, és nagysága: 𝐻_i = 2θ_i𝑁.

Másodrendű hatások

Az EN 1992-1-1 szabvány 5.8.8 fejezetében bemutatott módszer alapértelmezés szerint elkülönített, állandó keresztmetszetű és konstans normálerővel terhelt oszlopokra alkalmazható.

A méretezési módszer az oszlop másodrendű hatások következtében legnagyobb görbületet szenvedő pontjában egy maximálisan elképzelhető határgörbület segítségével meghatározott maximális másodrendű nyomatékot (𝑀₂) eredményez, aminek a hossz menti lefutását közvetlenül nem határozza meg. A biztonság és egyszerűség szempontjából szokás ezt a nyomatékot egyenletesen feltételezni a hossz mentén, de a szabvány megengedi a szinuszos vagy a parabola-szerű lefutást is.

Görbületeloszlásra vonatkozó reális feltételezések esetén az Eurocode megengedi a módszer használatát teljes szerkezetek esetén is (EN 1992-1-1 5.8.5 (3)), azonban ez kézi módszerek esetén általában nem lehetséges, az egyes elemek közötti interakciók miatt.

A módszer használatához elengedhetetlen a kihajlási hossz megadása, a másodrendű nyomaték nagysága függ tőle. Ehhez a szabvány megengedi a rugalmas elmélet során alkalmazott tényezők használatát (konzol esetén 𝑙₀ = 2𝐻, alul befogott - felül megtámasztott esetben 𝑙₀ = 0.7𝐻, stb.).

A hajlítónyomaték számítása:

𝑀_Ed = 𝑀_0Ed + 𝑀₂

ahol

𝑀_0Ed elsőrendű nyomaték, amely tartalmazza a méreteltérések (imperfekciók) hatását

𝑀₂ névleges másodrendű nyomaték (tartalmazza mindennemű görbület hatását).

Görbületből származó másodrendű nyomaték számítása

A másodrendű nyomaték számításához először a névleges görbületet kell meghatározni:

1/𝑟 = 𝐾_r𝐾_φ1/𝑟₀

ahol

• 𝐾_r normálerőtől függő csökkentő tényező
  
• 𝐾φ kúszás hatását figyelembe vevő növelő tényező
  
• 1/𝑟₀ tönkremenetelhez tartozó elméleti (fizikai) görbület

1/𝑟₀ = ε𝑦𝑑/0,45𝑑

A görbület ahhoz a ponthoz tartozik, amikor a beton eléri a határösszenyomódását ( ε𝑦𝑑 ) és a húzott betonacél éppen megfolyik, vagyis az úgynevezett „kiegyensúlyozott” eset.

Azt, hogy a teherbírási vonal melyik részén vagyunk a normálerőtől függő csökkentő tényező veszi figyelembe:

𝐾_r = (𝑛_u − 𝑛)/(𝑛_u − 𝑛_bal)

ahol

• 𝑛 = 𝑁_Ed / A_c𝑓_cd
  fajlagos normálerő
  
  • 𝑁_Ed
    normálerő tervezési értéke
    
• 𝑛_u=1+ω
  • ω = A_s𝑓_yd / A_c𝑓_cd
    mechanikai vashányad
    
  • A_s
    betonacélok teljes keresztmetszeti területe
    
  • Ac
    betonkeresztmetszet teljes területe (külső befoglaló méret)
    
• 𝑛_bal =0.4
  n értéke a legnagyobb nyomatéki teherbírásnál
  
• (0.4 alkalmazható bővebb információ hiányában)

A kúszást figyelembe vevő csökkentő tényező:

𝐾_φ = 1 + βφ_ef ≥ 1

ahol

• φ_ef = φ(∞,0) 𝑀_0Eqp / 𝑀_0Ed
  hatékony kúszási tényező
  
  • 𝑀_0Eqp elsőrendű hajlítónyomaték kváziállandó (használhatósági határállapot) kombináció alapján
    
  • 𝑀_0Ed elsőrendű hajlítónyomaték (teherbírási határállapotnak megfelelő) tervezési kombináció alapján
    
• β=0,35 + 𝑓_ck/200−λ/150
  
  • λ = 𝑙₀ / 𝑖
    karcsúság
    
  • 𝑙₀
    kihajlási hossz
    
  • i = √𝐼_c/𝐴_c
    repedésmentes betonkeresztmetszet inerciasugara

A másodrendű nyomaték

𝑀₂=𝑁_Ed𝑒₂

ahol

másodrendű külpontosság, ahol c a görbületeloszlástól függő tényező. Állandó keresztmetszet esetén 𝑐=𝜋² használható. Ez szinusz alakú görbületeloszlásnak felel meg. Állandó görbület esetén 𝑐=8 használható.

Méretezés

Teherbírási vonal

A teherbírási vonal értelmében a vasbeton oszlop nyomás-hajlítás interakciója során a tönkremenetel mindig akkor következik be, amikor a beton eléri az alakváltozási kapacitását (általában 𝜀_cd = 0,35%).

Ebben a pillanatban attól függően hol vagyunk a teherbírási görbén, a másik oldali acélbetét:

• húzott és már egy ideje folyik,
  
• húzott és éppen megfolyik,
  
• húzott, de rugalmas
  
• nyomott és rugalmas

A továbbfejlesztés elméleti háttere

A méretezési eljárás a 2. fejezetben ismertetett szabványos eljárás kiterjesztése. A kihajlási hosszok kézi megadását automatizálja, illetve megadja a másodrendű igénybevételek lefutását.

A számítás alapját szolgáló görbületeloszlás kiinduló értékét a globális szerkezeten végzi és nem egy elkülönített oszlopon. A görbületeloszlást a teljes szerkezeten számolt rugalmas kihajlási alakokból kiindulva határozza meg (Lineáris kihajlásvizsgálat - LBA).

Ez egy reális görbület eloszlásnak tekinthető a szerkezetre nézve, mert a teljes szerkezetre számolunk kihajlási alakokat, így figyelembe vesszük a szerkezetei elemek kölcsönhatását is. Ezzel a módszer kiterjeszthető, az oszlop már nemcsak elkülönített elemként, hanem a teljes szerkezet egy részeként lesz vizsgálható az Eurocode értelmében (EN 1992-1-1 5.8.5 (3)).

A végső lépést, a másodrendű nyomatékok (𝑀₂), meghatározását már elkülönített modellen végzi a szabvány szellemében, de ehhez a görbületi alaknak felhasználja a teljes modellen számított megfelelő kihajlási alaknak az adott oszlop mentén kapott értékeit.

A kihajlási alak maximum értékét a szabvány által előírt görbületre (1/𝑟) nagyítja, a többi értéket pedig ezzel arányosan változtatja.

A megfelelő sajátalak hozzárendelést egy Kihajlás-érzékenység vizsgálat nevű eljárás végzi. A nagyítást a sajátalak oszlop hossza mentén talált legnagyobb görbületi pontjában végzi el.

Ezzel a módszerrel elméletileg bármilyen szerkezeti elemre és a teljes szerkezetre képesek lennénk másodrendű nyomatékok számítására. Jelen fejlesztési fázisban azonban még csak vasbeton oszlopként definiált, egyenes tengelyű rúdelemeknél vesszük figyelembe.

Később, amennyiben igény mutatkozik rá, megfelelő tesztelés és verifikálás után, általános érvényűvé fejleszthető az eljárás. Ez igen hasznos funkció lehetne például vasbeton ívek, vagy nyomatékbíróan vasalt vasbeton keretállások esetén.

Kihajlás-érzékenység vizsgálat

A módszernél a legnagyobb nehézség, hogy egyes rúdelemeknek legyen mértékadó kihajlási alakja mindkét irányban (ha z a függőleges, akkor x és y irányban). A szerkezetnek a felhasználó által meghatározott számú sajátalakja kerül meghatározásra.

Minden egyes alakot, mint elmozdult alakot feltételezvén a szerkezet minden rúdeleme mentén kiszámoljuk rúdelemenként az összegzett deformációs energiát.

Az éppen vizsgált kihajlási hossz alapján számított legnagyobb deformációs energia értéket mutató elemhez 100% értéket rendelünk, a többi elemhez arányosított értéket. Az éppen vizsgált kihajlási alakot az annak megfelelő rúdelemhez rendelünk.

Mivel egy oszlop általánosságban a két merőleges irányban is kihajolhat, a vizsgálatot mindkét lokális irányban elvégezzük és egyetlen oszlophoz 2 sajátalakot rendelünk (irányonként 1-1).

Másodrendű nyomaték meghatározása

Az Eurocode szerint:

𝑀₂ = 𝑁_Ed𝑒₂

ahol 𝑐 = π₂

A ConSteel hasonlóképpen számol. A vasbeton oszlop minden végeseleméhez számolunk másodrendű nyomatékot. Ehhez három értéket használunk fel. Az első a végeselem pontban a normáligénybevétel (𝑁_Ed). A második az Eurocode szerint meghatározott másodrendű külpontosság (𝑒₂).

Ezek után a harmadik érték az adott végeselem pontban a kihajlási alak ordinátája, úgy, hogy a kihajlási alak maximumát egységnyire normáltuk. Ezzel a harmadik értékkel felszorozva az első kettőt kapjuk meg a vasbeton oszlop adott végeselem pontjában a másodrendű nyomatékot. Ez egy pontosított nyomatéki eloszlást eredményez.

Különbségek a szabványos eljáráshoz képest

Egyszerűsítés a hatékony kúszás számításánál:

φ_ef = φ(∞,𝑡₀)

konzervatív módon a hatékony kúszást egyenlővé tesszük a kúszási tényező végértékével, csökkentés nélkül. Ezzel elkerülve olyan hibákat, mint például, ha kváziállandó teherkombinációban nincs nyomaték, akkor a hatékony kúszási tényező értéke definíció szerint zérus.

Kúszási tényező értéke ConSteelben

A ConSteel-ben szereplő értékek a Vasbeton Szerkezetek Eurocode segédlet [6] 1. Táblázatából származnak.

Ez az EN 1992-1-1 3.1.4 fejezetét veszi alapul. Itt különböző tényezők segítségével meg lehet határozni a kúszási tényező végértékét, betonszilárdság függvényében, diagramok segítségével.

Karcsúság számítása kihajlás-vizsgálat alapján

Euler rúd kritikus ereje. A képletet átrendezve:

ahol

Nincs szükség a kihajlási hossz megadására, a karcsúság számítása automatizált.

Másodrendű nyomaték eloszlása kihajlási alak alapján

A másodrendű nyomaték eloszlása megegyezik a kihajlási alakéval, ezzel figyelembe véve az oszlopok közötti interakció is.

A módszer bemutatása konzolos példán keresztül

A modell létrehozásához szükséges információkat a Vasbeton oszlopok tervezése - Áttekintés című cikkünkben találod.

Vagy töltsd le a modellcsomagot a cikk végén található gombra kattintva és nyisd meg a "separate_circle_column_cantilever.csm" fájlt.

Elsőrendű analízis

Elmozdult alak: az értékek reálisnak tűnnek:

• kis mértékű függőleges elmozdulás
• abban az irányban, ahol nagyobb vízszintes terhet tettünk rá nagyobb elmozdulás
• másik irányban a rárakott imperfekció miatt kis elmozdulás
• az elmozdult alak a vártnak megfelelően a vízszintes teher irányában görbült

Ezután érdemes ellenőrizni az igénybevételeket

N

• függőleges teher értéke végig (nincs önsúly most)

negatív előjel -> nyomás

Vy+Mz

• normálerőből számoluk az imperfekciót
• 675*0,005 = 3,375 kN
• 3,38*3 = 10,14 kNm
• az alakok és az értékek is stimmelnek
• igénybevételből nincs Vy+Mz, csak imperfekcióból

Vz +My

• normálerőből számolunk az imperfekciót
• 675*0,005 = 3,375 kN
• 3,38*3 = 10,14 kNm
• Ezek az imperfekcióból számolt igénybevételek
• plusz hozzájön 20*1,5 = 30 kN teher
• 30+3,375 = 33,375 kNm
• 33,375*3 = 100,125 kNm
• ezek az igénybevételek is stimmelnek,
• elsőrendű igénybevétel terhekből + ferdeség

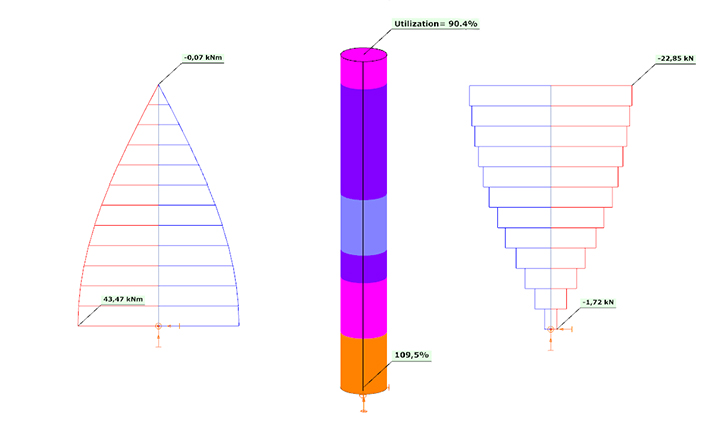
Kihajlás számítás és Kihajlás érzékenység

A koordinátákból látható, hogy síkbeli kihajlási esetről van szó.

Egy oszlop esetén viszonylag könnyű ellenőrizni, hogy van-e mindkét irányban mértékadó sajátalak. Itt most csak egy darabot sikerült számolni, úgyhogy biztos nincs.

Módosítani kell a kihajlásszámítás paramétereit. Érdemes növelni a releváns kihajlási sajátértékek felső határértékét, illetve a számolt kihajlási alakok számát.

Töltsd le a cikk végén található modellcsomagot és nyisd meg a módosított "separate_circle_column_cantilever_MoreBucklingShape.csm" modellfájlt.

Több kihajlási alakot számítva már van mindkét irányban.

Teherbírás számítás - EN 1992 szerinti feltétel

Most minden szimmetrikus.