Introduction

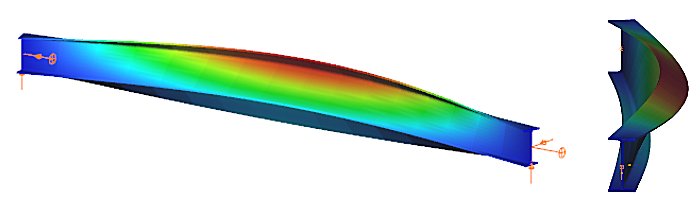
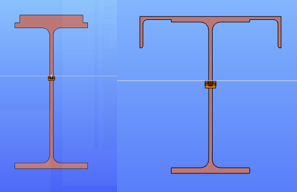
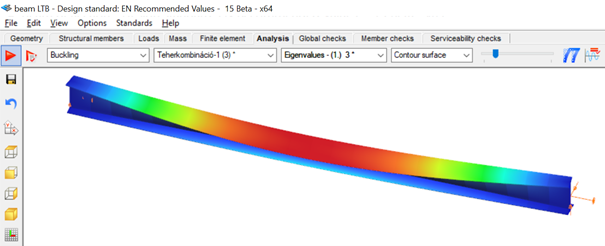
When a beam, bent in a plane, is allowed to move and twist freely between its two support points, in addition to bending, sudden perpendicular displacement and twisting may occur: causing the beam to deviate out of its original plane. This phenomenon is illustrated in Figure 1, showing a single supported beam with I-section bent around the strong axis. As the bending moment in the vertical plane increases, reaching a critical value, the beam undergoes abrupt lateral movement and twisting between the supports. This phenomenon is called lateral torsional buckling (LTB), which is a loss of stability mode that can apply to both perfect beams and real beams.

The design of the beam against LTB is fully analogous to the design of a compressed column against flexural buckling. The analogy is illustrated in Table 1, where the corresponding parameters are shown that affect the two buckling resistances:

Flexural (column) buckling	Lateral torsional buckling
design force ($N_{Ed}$)	design moment ($M_{Ed}$)
critical force ($N_{cr}$)	critical moment ($M_{cr}$)
column slenderness ($\frac{}{\lambda}$)	beam slenderness ($\frac{}{\lambda}_{LT}$)
buckling reduction factor ($\chi$)	buckling reduction factor ($\chi_{LT}$)
buckling resistance ($N_{b,Rd}$)	buckling resistance ($M_{b,Rd}$)

The critical moment of the perfect beam is determined at the location of the maximum value of the M_y,Ed design bending moment diagram. For a doubly symmetrical I cross-section:

$$M_{cr}=C_1\frac{\pi^2EI_z}{(k_z⋅L)^2}\left[\frac{I_\omega }{I_z}+ \frac{(k_zL)^2GI_t}{\pi^2EI_z}\right] ^{0.5} $$

where k_z is the coefficient of restraint about the weak axis of the cross-section, G is the shear modulus, and I_t and I_ω are the pure (St. Venant) and warping torsional moments of inertia of the cross-section. The value of the factor C₁ depends on the shape of the bending moment diagram and its value can be found in appropriate tables and manuals. For a constant moment diagram, C₁=1.0. The formula for the other design parameters, in particular the buckling reduction factor $\chi_{LT}$, depends on the design standard considered.

Lateral torsional buckling resistance by EN1993-1-1  

The design of the beam against LTB (load capacity check) according to EC3-1-1 shall be carried out in the following steps:

gate

Designing a lattice girder

The design of the bars of a truss (lattice girder) structure does not require any special theoretical knowledge: normally, the truss bars are designed as compressed and/or tensioned bars, neglecting bending moments and shear forces. The dimensioning of compression bars is nowadays carried out using a model-based computer procedure. For details, see the knowledge base material Design of columns against buckling. Here, only the determination of the deflection length of the compressed bars is presented.

The most important parameter for the dimensioning of a compressed bar is the slenderness:

$$\overline{\lambda}=\sqrt\frac{Af_y}{N_{cr}}$$

where

$$N_{cr}=\frac{\pi^2El}{(kL)^2}$$

where the buckling length factor k is recommended by EN1993-1-1 to facilitate manual calculations:

Type of the bar	Direction of buckling	k
chord	– in-plane – out-of-plane	0.9 0.9
bracing	– in-plane – out-of-plane	0.9 1.0

Software using model-based computational methods (e.g. Consteel software) determines the elastic critical force N_cr directly by finite element numerical methods, taking into account the behaviour of the entire lattice girder, instead of the above conservative formula. The following example is intended to illustrate the relationship between the manual design procedure proposed by the standard and the results of the modern model-based numerical procedure.

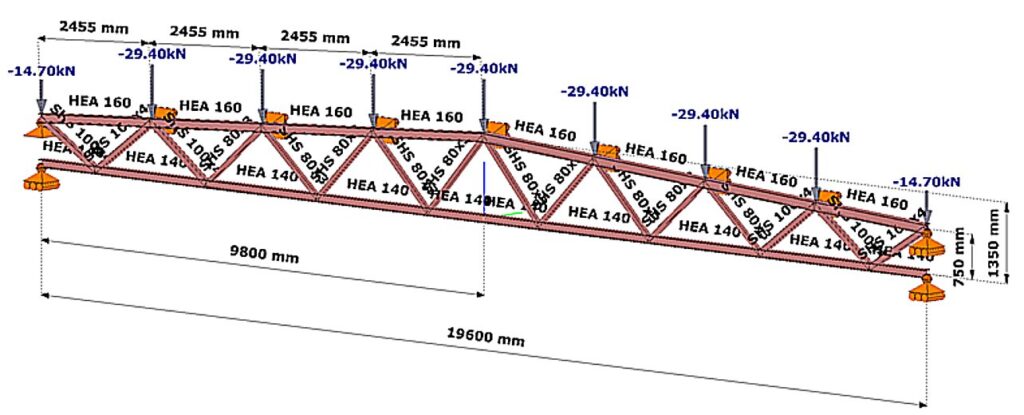
• Let the structural model of the lattice girder under consideration be the Consteel model shown in Figure 1.
• Let the load shown correspond to the design load combination of the girder.
• Determine the deflection length of the most stressed compressed chord member using finite element numerical stability analysis.

Relationship between procedures

The steps of the calculation are:

Buckling stability analysis

The stability analysis of the elastic model shows the governing buckling mode of the lattice structure and the corresponding elastic critical load factor α_cr (Figure 2).

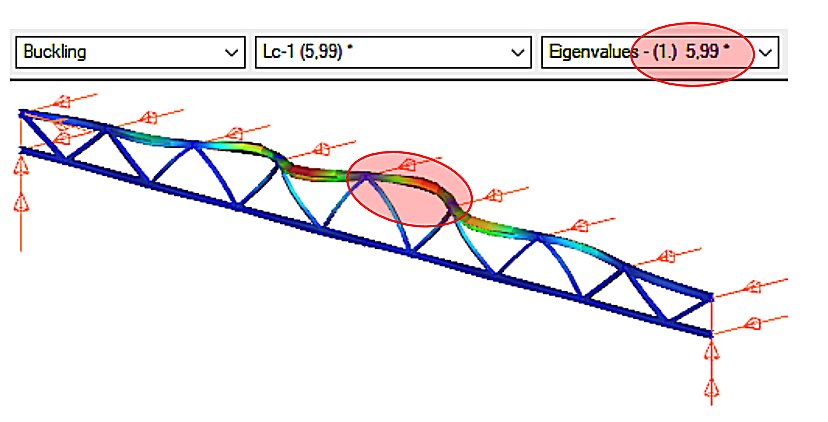
We can see that the upper chord of the perfectly elastic model is deflected laterally under load. The load that causes this elastic buckling is the critical load, whose value is given by the product of the design load and the critical load factor α_cr=5.99.

gate

This overview delves into Consteel’s solution, offering an alternative approach to calculating effective cross-sectional properties and reshaping conventional methodologies in structural analysis and design.

Determine the strength utilization of a double symmetric welded I cross-section with 384×4 web and 300×8 flanges, if the internal forces on the cross-section are N_Ed=500kN compressive force and M_y,Ed=100kNm bending moment. The material grade of the cross section is S235.

Calculation of cross-sectional properties

First, take the cross-section data (symmetric welded I-section), from which the Consteel software generates the EPS (and GSS) (see Online Manual/10.1.1 The EPS model) cross-section model (Fig. 1).

If the cross-section is class 4, the effective model is determined by the assumed normal stress distribution. According to EC3-1-1, the EPS model of a class 4 cross-section can be defined in two ways :

– method A: based on pure stress conditions,

– method B: based on complex stress condition.

In order to compare the results, the cross-section properties will be calculated by method A at first and then by method B.

Cross-sectional properties by method A

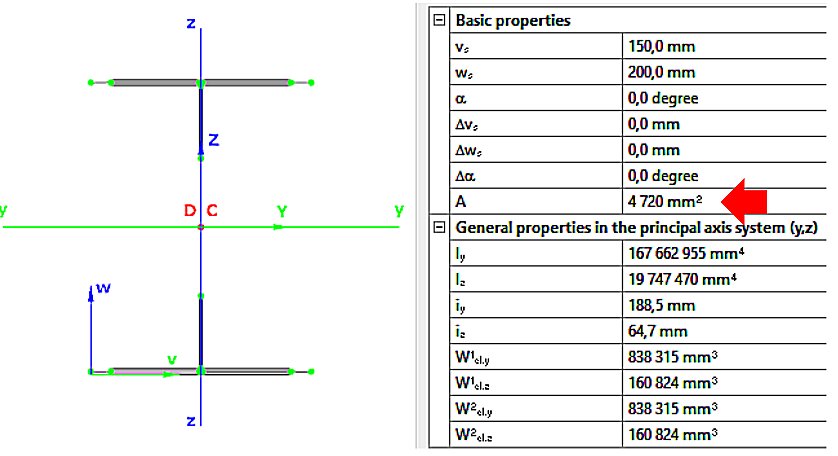
• pure compression N_Ed  (Fig. 2): 

A_eff=4720mm²   

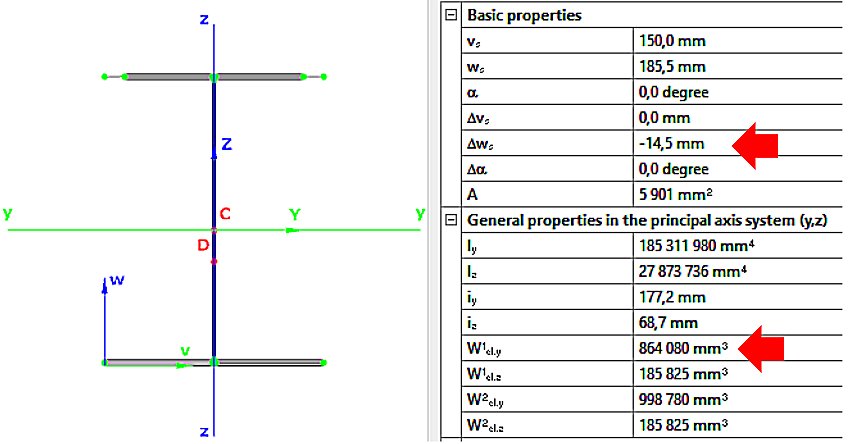
• pure bending M_y,Ed  (Fig. 3): 

W_eff,y,min=864080mm³

e_z=14.5mm 

Cross-sectional properties by method B

GATE

Introduction

During the lifetime of a steel structure changes often happen. These changes usually result an increase of loads acting on some of its elements which therefore may need to be strengthened.

Strengthening is usually done by welding additional steel plates to the existing members. In the case of I sections, usually, the flanges are reinforced to increase the bending moment capacity or the web is stiffened to avoid local buckling or crippling at support regions.

This paper will focus on the increase of bending moment capacity.

Lateral-torsional buckling resistance

The usual practice is to either increase the compression flange thickness by adding additional plates to it, or by widening it with the help of angles, as can be seen in the pictures below.

Although these can be very efficient ways to increase the bending moment capacity of a beam, welding on site is a complex process and might require the temporary removal of structural or non-structural elements connected to the flange of the beam. Welding especially “above the head” is difficult, the quality of weld seam needs to be properly checked.

Bending moment capacity of a beam might be limited by lateral-torsional buckling. If the section is not sufficiently restrained laterally against torsion, its actual load-bearing capacity will be lower than the value which depends purely on its section resistance.

In such cases, if the LTB behaviour could be directly improved, there would be no need to strengthen its cross-section along its full length. Here comes the Superbeam as a possible help.

Additional lateral restraining elements are often difficult to be added, therefore this is often not an option.

If we look at what LTB resistance of an I section depends on, we can see, that if we don’t want to change its cross section along its full length, it depends on the value of the reduction factor responsible to consider lateral-torsional buckling χ_LT.

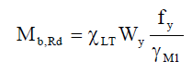
This reduction factor is calculated from the slenderness value of the beam, which needs to be improved (reduced) to result a lower, more favourable reduction factor.

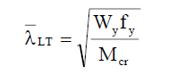
Without changing the cross section, the only way to do this is by improving the critical moment value. Increasing this value can be made not only by changing the cross-section but also by changing the boundary conditions.

The value of parameters ‘k’ and ‘kw’ depend on the boundary conditions, where ‘k’ means a factor which depends on how the section is fixed against weak axis bending at its ends and ‘kw’ means a factor which depends on how the section is fixed against warping. Warping is the phenomenon when the upper and lower flange of an I section twist in opposite directions.

To change the end conditions is typically difficult, but a certain limitation of the twist of flanges relative to each other ie. preventing or limiting warping might be possible. Limitation of this twist can be obtained by connecting the flanges by an additional element which has non-zero torsional stiffness. This torsional stiffness will prevent the counter-rotation of the flanges and therefore the warping and allowing to consider a ‘kw’ value different than 1.0 in this formula.

Consteel supports several such strengthening profiles and can determine the torsional stiffness to be considered in preventing or limiting warping.

Analysis with Consteel Superbeam

Let’s take the following case. We have a simple supported 5 m long beam loaded by a uniform load of 20 kN/m acting at the top flange, on top of its self weight, without any intermediate lateral support. Its section is a welded I profile, made of S235, 10 mm thick plates, flange width of 200 mm and total section depth of 320 mm.

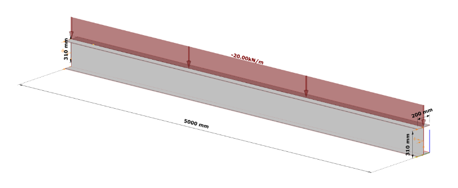
As we can expect, in the case of such a large unbraced length, the bending moment resistance would be strongly limited by lateral-torsional buckling, and therefore we can expect that strengthening by the proposed method is viable.

The critical moment of this beam is obtained in Consteel using linear buckling analysis with 7DOF beam elements option of the Superbeam, which has found the critical multiplier of 2.88.

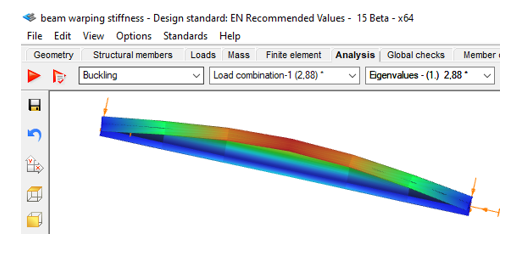
This results M_cr = 2.88*64.18=184,84 kNm and a slenderness λ of 1,036 and reduction factor of 0,519.

The final bending moment resistance is 103 kNm.

Let’s further assume that this resistance needs to be increased by 30% due to new requirements. Let’s see whether a successful strengthening without modifications of the cross-section would be possible.

gate

Introduction

Beam with welded I sections are often executed with slender webs. This is mainly due to the recognition that the main contributors to bending stiffness of a beam are the flanges. The web plate’s main role is to safely keep these flanges away from each other and carry the shear stresses which might be present. Significant weight saving can be achieved with the use of slender webs, but there are some aspects to take care about.

When slender web plates are exposed to longitudinal, uniform normal stresses, above a certain stress level its distribution will no longer remain uniform. A compressed region of a plate distant from its lateral supports may buckle in a direction perpendicular to the acting external normal stresses, causing a subsequent transfer of stresses from the affected region to other neighbouring regions remaining in their unbuckled position.

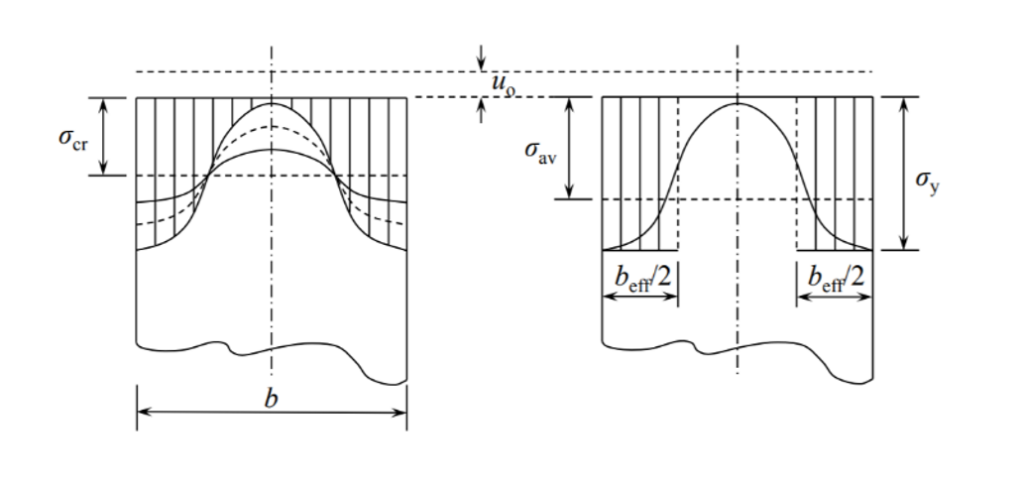
This buckling remains limited to a part of the plate keeping other parts intact and therefore is called as local buckling. Local buckling usually does not result an immediate collapse of the structure, due to possibility of the stresses to redistribute and often even a substantial amount of further load increases are possible.

The tendency of a compressed plate to suffer local buckling is characterized by its slenderness value defined by the following formula

where σ_cr is the critical stress level above of which the stress redistribution and local buckling starts to appear. A higher critical stress will result in lower slenderness value which indicates that the plate can carry higher compressive stresses without the initiation of local buckling.

Analysis of cross-sections with beam finite elements

The well-known beam finite elements used by usual structural design software do not “see” the internal composition of the cross-section. During structural analysis the sections are represented by certain integrated cross-sections properties assuming the validity of several assumptions including the Bernoulli-Navier Hypothesis and the non-deformability of the cross-section. A local buckling of any of its internal plates would violate these assumptions making hard to create the equivalent cross-sections properties.

In the modern design practice followed by Eurocode the phenomenon of local buckling is handled by the use of effective section properties. Regions subject to possible local buckling of compressed plates of a cross-sections are “eliminated” and the section properties are calculated based on the remaining parts of the cross-sections.

Design verifications use these effective cross-section properties to calculate the resistance of cross-sections exposed compressive forces. When required by Eurocode, the effect of appearance of local buckling can also be reflected in a structural analysis using beam finite elements with the use of effective cross-section properties, instead of the original gross section properties. This is mainly required to prove serviceability criteria.

Analysis of cross-sections with Consteel Superbeam

The Consteel Superbeam function makes possible to confirm directly the presence of local buckling using the same beam element based model, but using a mixed beam and shell finite element modelling and analysis approach. Using the Superbeam tool, complete structural members or parts of them can be alternatively modelled with shell elements and the rest can still be modelled with beam finite elements. Using this technique, the total degrees of freedom of the model can be kept as low as possible. When using Superbeam, the designer has the choice whether to use beam or shell finite elements, as appropriate.

Contrary to beam finite elements, modelling with shell finite elements doesn’t have the previously mentioned limitations. This approach can fully consider the shape and location of the cross-section’s internal components instead of the use of an integrated overall section property. When a linear buckling analysis (LBA) is performed, the critical stress multipliers corresponding to the actual stress distribution can be obtained. Additionally to the load multipliers, the corresponding buckling shapes are also available, giving direct indication on the location, shape and appearance of local buckling within the compressed parts of the cross-section.

The use of effective cross-section concept is very convenient but there might be cases when more insight view is desired. The following example gives an idea where the Superbeam function can be helpful.

Demonstrative example

Let’s consider a 12 m long simple supported welded beam with the following parameters

The beam is laterally restrained at third points at the level of its upper flange. The beam is loaded with its self-weight plus a uniformly distributed load of 10 kN/m acting at the level of upper flange.

When the beam is analysed with 7DOF beam finite elements, one can obtain the critical load multiplier of 5.2 of the global buckling mode, which is lateral-torsional buckling (LTB) in this case.

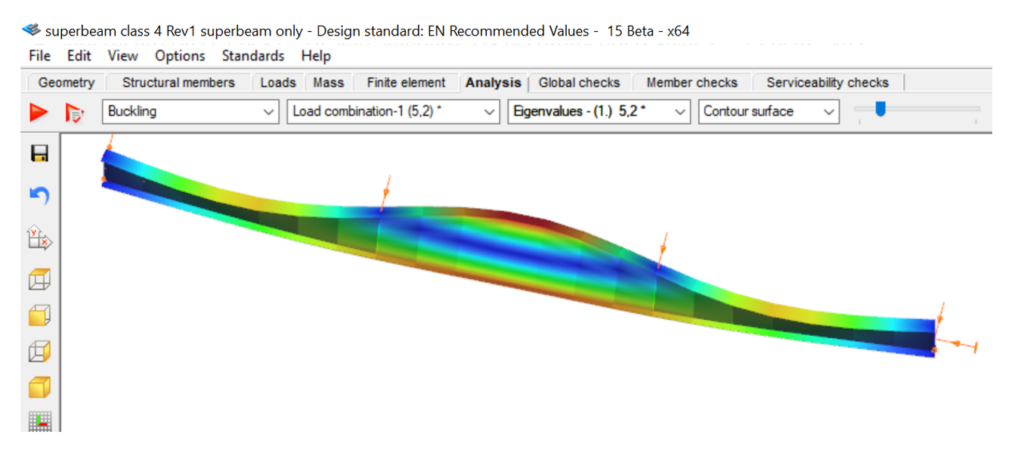
The beam finite element cannot give any visible indication about possible local buckling in compressed plates of the cross-sections.

As the maximum bending moment occurs in the middle third of this beam, it seems enough to analyse this part mode deeply with the Superbeam function. An LBA with the mixed beam and shell model gives comparable critical multiplier of 5.22 with some numeric perturbances in the part modelled with shell elements.

gate

Introduction

Are you wondering how a web opening would influence the lateral-torsional buckling resistance of your beam? Check it precisely with a Consteel Superbeam based analysis

It is often required to let services pass through the web of beams. In such cases the common solution is to provide the required number of opening in the webplate. Such an opening can have a circular or rectangular shape, depending on the amount, size and shape of pipes or ventilation or cable trays.

Beams must be designed to have the required against lateral-torsional buckling. The design procedure defined in Eurocode 3 is based on the evaluation of the critical bending moment value which provides the slenderness value, needed to calculate the reduction factor used for the design verification.

There is no analytical formula provided in the code for beams with web openings. Would the neglection of such cutouts cause a miscalculated and unsafe estimation of the critical moment value?

The following demonstration will be made with a 6 meters long simple supported floor beam with a welded section.

Exposed to a linear load of 10 kN/m, the critical bending moment value of the solid web beam can be obtained by performing a Linear Buckling Analysis (LBA) with Consteel.

Download model file

The obtained critical multiplier for the first buckling mode is 3.00 which means that the actually applied load intensity can be multiplied by 3.00 to reach the critical load level. The corresponding critical moment will have the value of M_cr = 3.0 * 47.18 = 141.54 kNm yielding a slenderness of 1.286 (M_pl,Rd = 234.20 kNm) and a lateral-torsional buckling resistance of 0.394 * 234.20 = 92.27 kNm. With this value the actual utilization ratio is at 51%.

How would this value change if a rectangular opening needs to be cut into the web of this beam?

Analytical formula for critical bending moment

By looking to the analytical formula (ENV 1993-1-1 F.4) to calculate the critical moment of double symmetric sections loaded at eccentric load application point it becomes obvious that the section properties having effect on the moment value are I_z, I_w and I_t.

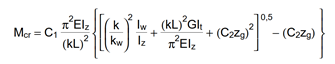
An opening in the web has no effect on the first two values and has very little effect on the last one. As it has been already shown in previous article, the presence of such an opening can have effect on the vertical deflection, but as long as the lateral stiffness of a beam is much lower than it’s strong axis stiffness, the vertical deflections can be neglected when the lateral-torsional buckling resistance is calculated. The usual linear buckling analysis (LBA) performed also by Consteel neglects the pre-buckling deformations.

Therefore one can expect that in general web openings can be disregarded when the critical moment value is calculated.

Analysis with Consteel Superbeam

Beam finite elements cannot natively consider the presence of web openings. In order to obtain the precise analysis result, it is possible to use shell finite elements. The new Superbeam functionality comes as a solution in such cases. Instead of using beam finite elements, let’s use shell elements!

Opening can be positioned easily along the web, either as an individual opening or as a group of openings placed equidistantly. The opening can be rectangular, circular or even hexagonal. Circular openings can be completed with an additional circular ring stiffener.

The rectangular opening for this example can be easily defined with this tool. As there is no need to provide any additional opening on the remaining part of the beam, only the first part which includes the opening will be modelled with shell elements and the rest can still be modelled with beam finite elements. Using this technique, the total degrees of freedom of the model can be kept as low as possible. When using Superbeam, the designer has the choice whether to use beam or shell finite elements, as appropriate.

gate

Web openings and their deflection effect on beams

It is often required to let services pass through the web of beams. In such cases, the common solution is to provide the required number of openings in the web plate. Such an opening can have a circular or rectangular shape, depending on the amount, size and shape of pipes or ventilation or cable trays. 

If the structural engineer has the freedom to position these openings along the beam, where to place them? What would be its effect on the deflection of the beam? 

The effect of such openings on the deflection is more important when the length of the opening along the beam is increased. As circular openings are made with equal length and depth, they are usually less critical than rectangular openings. 

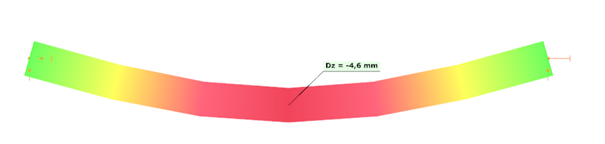
The following demonstration will be made with a 6 meters long simple supported floor beam with a welded section.

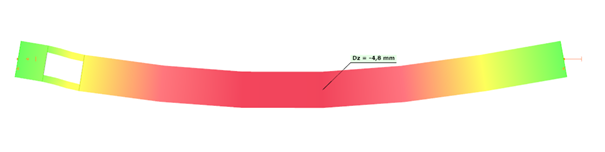
Exposed to a linear load of 10 kN/m, the deflection at mid-span of the solid web beam is 4.6 mm.

Download model file

Let’s assume that a 250 mm deep rectangular opening with a length of 400 mm needs to be provided on the web, at a distance of 300 mm from the left support.

Traditional analysis with beam finite elements

Consteel 7DOF beam finite elements are very powerful, but cannot consider natively such opening. The usual approach is to build a Vierendeel-type of model, by using additional beam elements with a T shape section „above” and „below” the opening. These additional beam elements are defined eccentrically to the reference line of the solid-web beam.

Eccentricities can be easily defined in Consteel using both smart and traditional link elements.

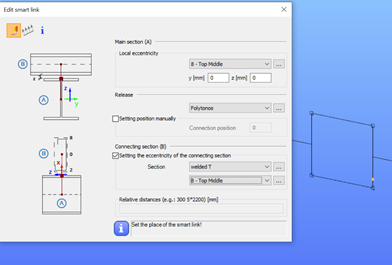
The deflection with this refined model will be equal to 4.8 mm.

Download model file

Analysis with Consteel Superbeam – use shell elements for more precise analysis results

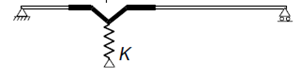
gate

In our series we have shown in Part 1 and Part 2 how the spring stiffness „K” is determined for and edge and for an intermediate stiffener. In this part we will show how to proceed further.

The goal is to determine how efficiently can this stiffener support the connected compressed plate. To consider local buckling of the compressed plate the effective widths will be calculated. These widths can be either calculated for a plate supported at both ends or for a plate supported at one end only, using Table 4.1 and Table 4.2, respectively. 

If a stiffener fulfills the minimum constructive requirements, we will first assume that it is rigid enough the act as a support. Based on this we work out the effective lengths for the connected compressed plates, assuming also that they are fully loaded up to the yield strength. Once we know the effective widths of the plate parts connected to the stiffener, we also know the load this stiffener is supposed to be able to carry without buckling, to justify the first assumption. Therefore, next we calculate the flexural buckling resistance of the stiffener. If we find out that it is lower than what was implicitly assumed previously, we go back to the first step, lower the stress to be compatible with the obtained buckling resistance of the stiffener (distortional buckling). This lower stress level may of course result different effective widths. An iterative procedure is started until the satisfactory result is found. After completion the final stiffener buckling resistance value will be incorporated into an equivalent effective thickness applicable for the stiffener and the connected effective plate parts.

In the above described iterative process the „K” value of the stiffener will be needed to determine the flexural buckling resistance of the stiffener. This resistance will be calculated using the help of a simple beam model, where the stabilization provided the remaining parts of the section is used as a continuous bedding of „K”. The cross section of the beam corresponds to the stiffener and connected plate parts and will be exposed to the actual stress level of the iteration, assumed as a simplification to be constant along the length. The length of the beam in this model is unknown at the moment, it should be equal to the half wavelength of the buckling shape which is expected to be around 1.5-3 times the height of the studied cold-formed section.

Distortional buckling will appear only if the length of the stiffener is much longer than this typical length range. As a further simplification Eurocode assumes infinite length as the possible worst case, because for this condition an analytic solution exists in the literature:

In this formula „K” is the spring value – shown in Part 1 and Part 2 – represents the spring stiffness value what the remaining section can provide to the stiffener. I_sand A_sare section properties of the corresponding stiffener together with connected effective widths of supported plates, namely area and inertia around an axis perpendicular to the expected direction of buckling of the stiffener. E is the Young modulus of the steel material.

The formula gives the critical stress level where elastic buckling would appear. Once this has been found, reduced slenderness is calculated, and the distortional buckling resistance can be obtained by using a special buckling curve given by (5.12a-c) formulas of EN 1993-1-3.

The validity of formula (5.15) can be easily demonstrated with a simple Consteel model.

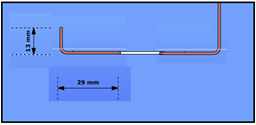
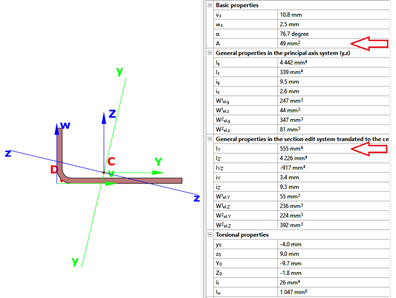
Let’s assume the Z section from our 1st blog exposed to compression force and let’s assume that we have already calculated effective width values. Yield strength of the material is 235 MPa and coating thickness is 0.04 mm. We found that the effective width of the lip and flange are c_eff=13 mm and b_eff=29 mm, respectively.

The section properties can be calculated with Consteel

gate

Distortional buckling – Further secret formulas of EN 1993-1-3. Check our article for the first secret formula if you hadn’t read it yet.

In our series we continue with the second „secret” formula of EN 1993-1-3.

This formula (5.11) is used when the ability of an intermediate stiffener to stabilize a compressed web plate is studied. 

When the intermediate stiffener is rigid enough, it divides efficiently the longer web plate into shorter plates. During buckling a rigid stiffener will not displace and the plate will buckle between the ends (stabilized by flanges) and this stiffener:

If the stiffener is not rigid enough, already at a much lower stress level the distortional buckling will appear which is characterized by a displacement of the stiffener and by the web plate buckling with a half-wave equal to the plate length:

In such a case Eurocode still accepts that web plate buckling will occur between ends and intermediate stiffener, but reduces the thickness of the intermediate stiffener zone, to compensate for the less than ideal rigidity. This compensation will depend on the buckling resistance of the stiffener when subject to compression.

The simplified model used by Eurocode in the procedure can be seen below. As a simplification it is assumed that the web plate is connected to the rest of the section with hinges. It means that it’s buckling shape is not influenced by the stiffness of connected parts, they do not encaster its ends, its ends can freely rotate. The ends of the plate are supported and there the plate can provide an elastic bedding to the stiffener, which will be considered as a „help” when its buckling resistance will be determined. This bedding is represented by the K spring stiffness:

The spring value which represents in this model the bedding provided by the plate is calculated as the ratio of the displacement obtained from the application of a unit load at the center of gravity of the stiffneer. In this case the unit load is applied perpendicularly to the web plate. Formula (5.11) gives the deflection (δ) from such unit load (u).

gate

Part 2 – Imperfection factors

The Eurocode EN 1993-1-1 offers basically two methods for the buckling verification of members:

(1) based on buckling reduction factors (buckling curves) and

(2) based on equivalent geometrical imperfections.

In the first part of this article, we reviewed the utilization difference and showed the relationship between the two methods. It was concluded that the method of chapters 6.3.1 (reduction factor) and 5.3.2 (11) (buckling mode based equivalent imperfection) are consistent at the load level equal to the buckling resistance of the member, so when the member utilization is 100%. The basic result of the procedure in 5.3.2 (11) is the amplitude (largest deflection value) of the equivalent geometrical imperfection. However, the Eurocode gives another simpler alternative for the calculation of this amplitude for compressed members in section 5.3.2(3) b) in Table 5.1, where the amplitude of an initial bow is defined as a portion of the member length for each buckling curves (Fig. 1.). We use the first column (“elastic analysis”) including smaller amplitude values.

It is an obvious expectation that these two standard procedures should yield at least similar results for the same problem. However, this is by far not the case in general.

In order to show the significance of the imperfection amplitudes this part is dealing with these two calculation methods, the variation of their values and the effect on the buckling utilization.

Let’s see again the simple example of Part 1: a simply supported, compressed column with a Class 2 cross-section (plastic resistance calculation allowed). The column is 6 meters high and has an IPE300 cross-section made of S235 steel. The two methods are implemented into Consteel and on Figure 2. it can be seen, that the two values for the amplitude of the geometrical imperfection is very different – e₀ = 24 mm by the 5.3.2(3) b) Table 5.1 (L/250) and e₀ = 13,4 mm by the 5.3.2 (11) (same as in Part 1).

gate