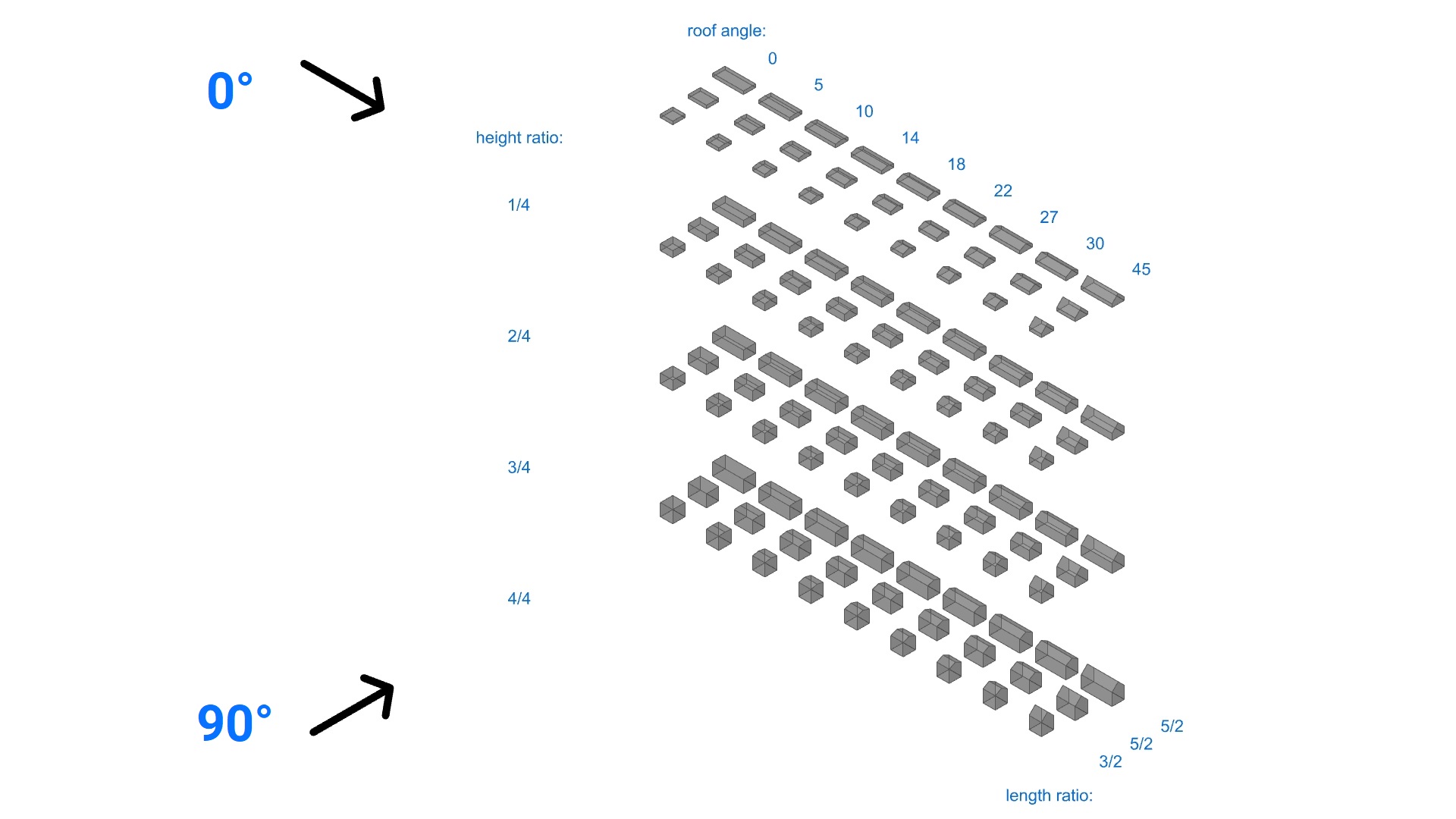
This study explores how Computational Fluid Dynamics (CFD)–based pressure simulation results can be compared and aligned with wind tunnel experiments and standardized design methods, reflecting the practical process engineers follow when assessing wind loads. The aim is to provide a framework for interpreting and applying simulation outputs with more confidence, supported by a clear workflow. To ensure that the findings are robust and generalizable, the analysis is grounded in a comprehensive parametric dataset: the Tokyo Polytechnic University (TPU) database of isolated low-rise buildings without eaves. This resource contains detailed pressure coefficient data for 116 building models—featuring flat, gable, and hip roofs—tested under eight wind directions, yielding more than 800 individual cases for comparison. To align these wind tunnel tests with the standard procedures the main orthogonal directions were investigated.
Compliance with standards
Before validating CFD results against established references, it is important to set the Eurocode baseline for wind load evaluation. From the wind effect side, a previous article covers how the specific wind profiles are determined and harmonized with the simulations during the preprocess phase, while for wind actions the Eurocode defines two main approaches:
- Wind pressure on surfaces – expressed through pressure coefficients for a range of building geometries.
- Wind forces on special structures – i.e. lattice towers.
Since CFD inherently produces surface pressure distributions, this study focuses exclusively on the first approach—wind pressure on surfaces—applied to closed buildings. For the purposes of this comparison, only vertical walls and simple roof types (flat and duopitched) were considered.
Under Eurocode procedures, building surfaces are subdivided into zones whose dimensions are determined by the building’s proportions. In practice, the characteristic zoning length, e , defines the extent of the regions for which local pressure coefficients are specified.
Therefore, to ensure a coherent comparison between wind tunnel tests and simulation results, the mesh refinement must be adjusted accordingly, for each previously presented geometrical case of the dataset for both principal orthogonal directions, which in turn makes a parametric study indispensable.
Parametric methodology
To support the parametric study, a dedicated script was developed to generate results for all three scenarios simultaneously: wind tunnel tests, simulation outputs, and standard-based approaches.
gateIn this article, we will explore pressure-based validation techniques applied to a simple block model within the context of wind simulation for structural engineering. Building upon our previous discussions on data processing and velocity-based validation, we aim to provide a comprehensive understanding of how pressure data can be utilized to ensure accurate and reliable wind surface loads from simulation results.
Pressure-based validation is a critical aspect of wind simulation, as it directly relates to the forces exerted on structures. During previous velocity-based validations [1] comparing the results (the average directional deviances of the velocity vector as a percentage) against established benchmarks showed that k-ε turbulence model produced the best results. Using the same simulations results the pressure-side comparison is presented below.
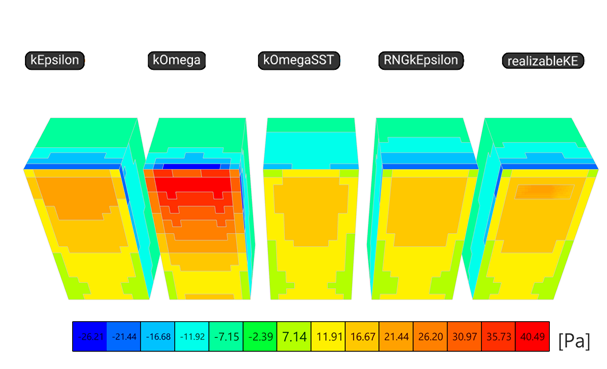
First, there is a significant difference between the simulation runtime and the iteration number, which was set to a maximum of 1000 iterations. The table below shows that the k-ε is the quickest, while k-ω SST and RNGk has not actually reached convergence. However, when comparing the global reactions calculated according to the pressure results the results are relatively close, more for the suctions on the top (Rz) and on the side walls (Ry), but less for the Rx (resulted by the pressure on the windward and the suction on the leeward walls), especially for k-ω.
Note: the Ry+ is only the resultant for one side wall of the cuboid, because the other side eliminates it, resulting a global reaction of Ry = 0 kN
| Load size [m] | 4 | ||||
| Turbulence Model | k-ε | k-ω | k-ω SST | RNGk | realizable k-ε |
| Runtime [s] | 135.295 | 392.686 | 707.589 | 663.564 | 440.801 |
| Iteration [-] | 197 | 413 | 1000 | 1000 | 342 |
| Rx [kN] | 195.63 | 315.59 | 179.88 | 176.23 | 180.22 |
| Ry+ [kN] | 94.54 | 97.75 | 92.98 | 96.95 | 95.73 |
| Rz [kN] | 53.47 | 50.02 | 52.74 | 58.64 | 54.33 |
| ADD [%] | 5.86 | 5.83 | 9.45 | 6.58 | 6.03 |
To conclude regarding the suitable turbulence models and to carry out relevant pressure-based validations it is preferable to use wind tunnel results adressing this topic directly. One of the earliest results [2] in this field by Baines, which forms the basis for the standards used today and a relatively new, thorough examination [3] by the Tokyo Polytechnic University is used as a starting point.
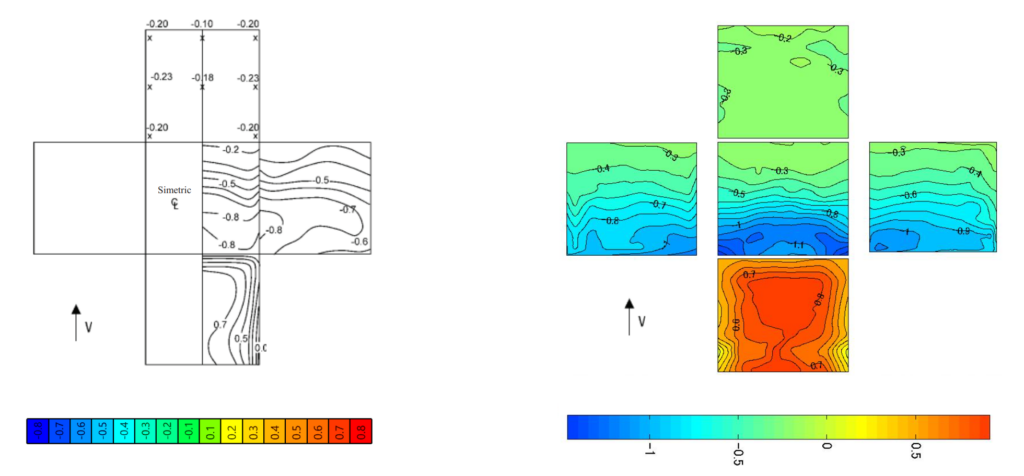
To process these results special tools were developed. The results by Baines in lack of any database was reproduced using the contour lines from the original image, while for the TPU experiment mean result values from actual measurement point results were processed in Grasshopper’s parametric environment.
Note: the color gradient for the result represenation is not harmonized according to the pressure coefficient results.
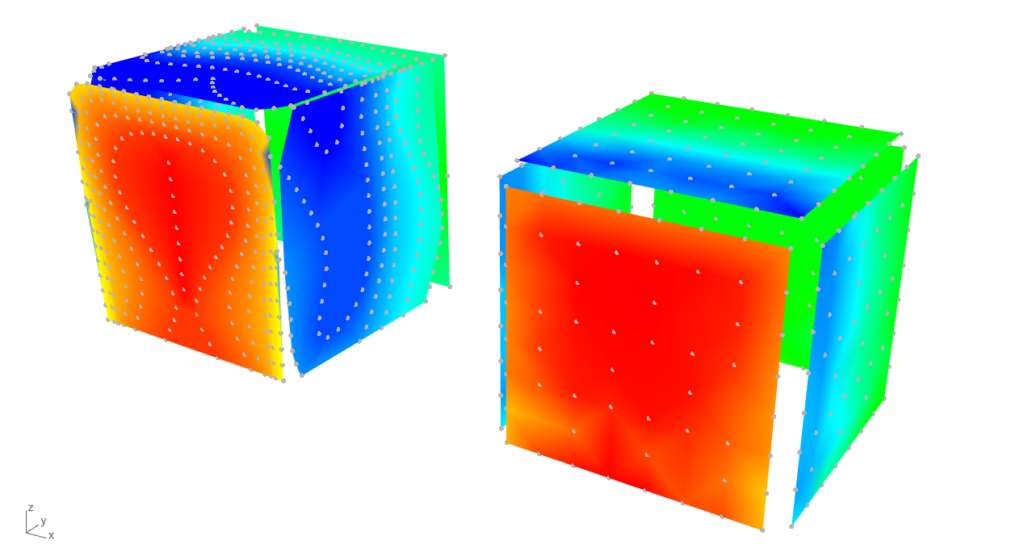
The mesh resulted by the points from the TPU results indicates an average edge length to start performing simulations. For this cuboid of 16 m x 16 m x 16 m, the ‘mesh size on the structure’ , or in other word the face edge length is 2.28 m, resulting a unified mesh suitable for post-process. For the refinement of the calculation domain a ‘mesh refinement factor’ of r = 2 was selected to reach an inlet face size below the reference height of 16 m (2.28 x 2r = 9.12 < 16). Regarding the wind profile, based on the TPU experiment, according to the Eurocode [4] a category III terrain was selected which is similar in turbulence intensity (Iv(zref) = 0.25). For the basic wind velocity, vb = 28.3 m/s was taken to produce a peak velocity pressure, qp(zref) = 1 kN/m2 for easier conversion between pressure coefficients (cpe) and surface wind loads (we).
Note: the color gradient for the result represenation of all six cases below is harmonized according to the surface load results. The values with bold are the peak (min or max) values for the windward, top, and side surface, while the narrow font represents the mean value. The axis system in front is representing the resultants of the surface loads.
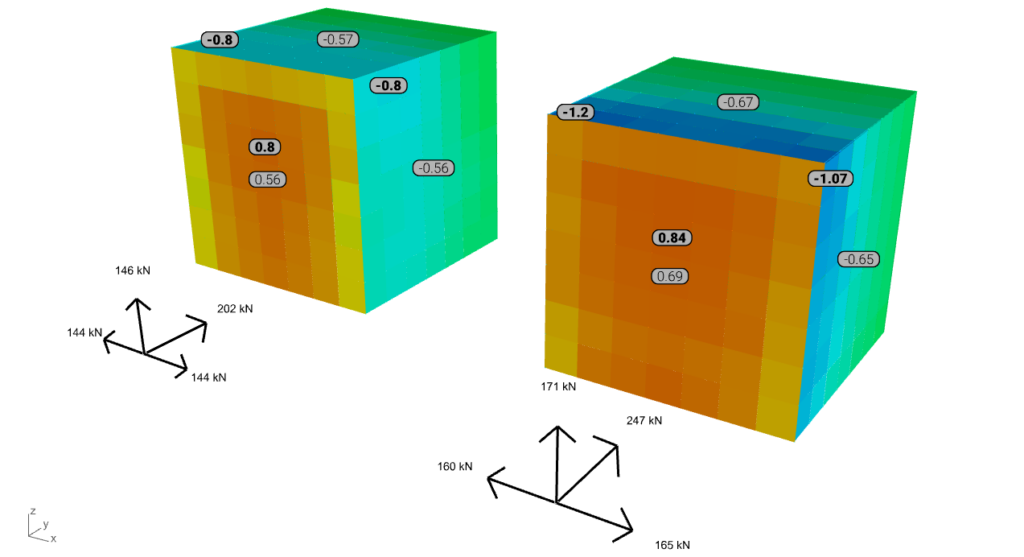
Upon projecting the experimental data onto the post-process mesh based on mesh vertex proximity, it was observed that the results from Baines are generally lower. This discrepancy is likely due to reduced accuracy at the edges and, more notably, at the corners. However, on the windward side, the maximum pressure coefficient is approximately 0.8, while the suction values also align with typical Eurocode values.
When examining global reactions or resultants, the simulation outcomes tend to align with the TPU results, especially on the windward side. Conversely, for the suctioned surfaces, such as the side walls and top, the simulation results are generally lower on average.
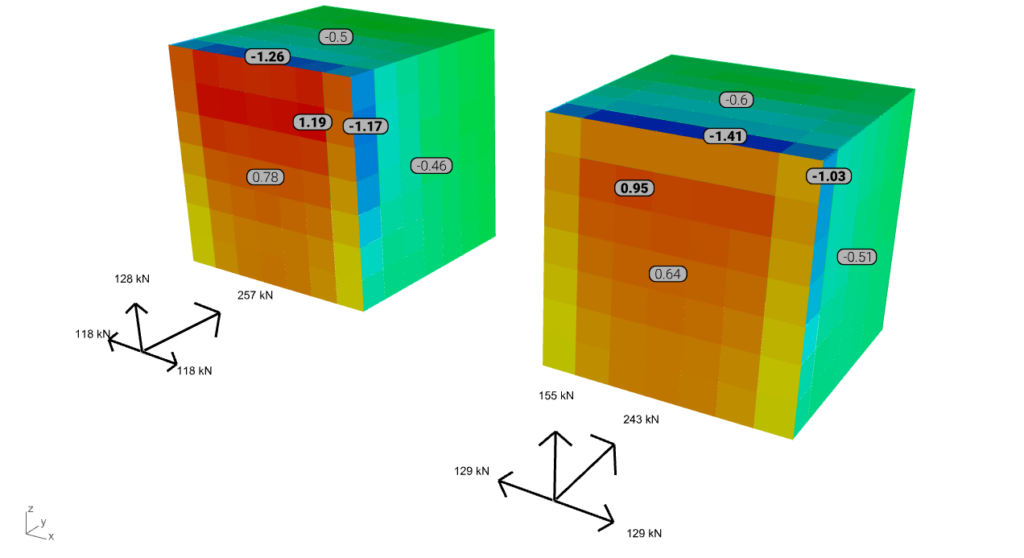
From the perspective of this pressure-based validation k-ω SST demonstrates improved accuracy, particularly when the ‘mesh size on the structure’ is refined to 1 meter. This refinement enhances the correlation of results, including on the suction sides. However, the model’s robustness can be questionable, leading to increased computational time for convergence.
For structural engineering purposes the zoning of these loads can actually offer efficiently usable loads during structural analysis, comparable with standards. From this scenario two advantages of simulated loads can already be observed:
- For the windward side loads with similar distribution to the wind tunnel experiment can be produced, leading to reduced loads instead of one uniformly distributed surface load (D zone of Eurocode)
- For the side walls the decrease of the loads along the height can also be produced with simulation, leading to reduced load areas for A zones of Eurocode
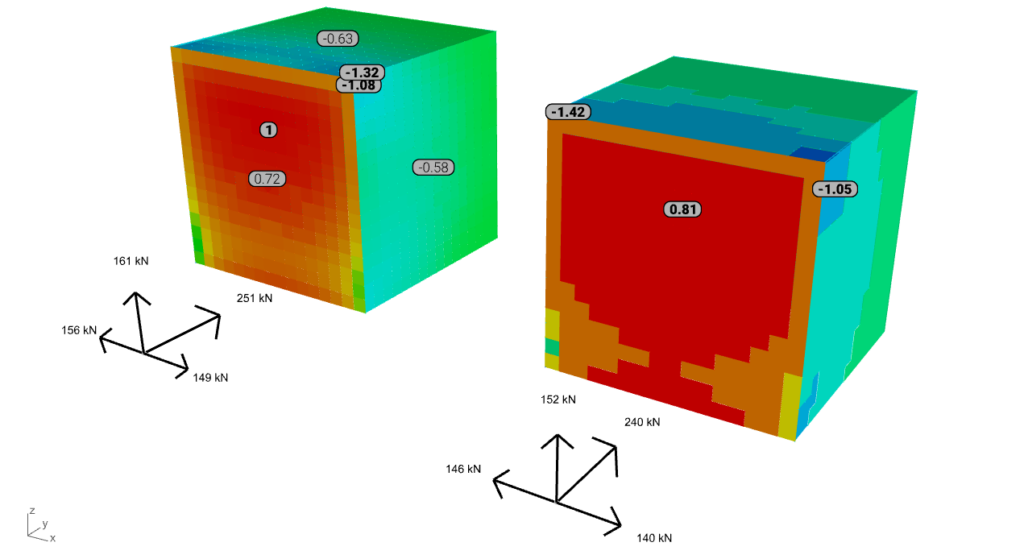
While obtaining wind tunnel experiment data for thorough, double-checked validation can be challenging due to limited background information, our current validations already highlight that mesh density and the appropriate selection of turbulence models are pivotal factors significantly affecting pressure distribution. Striking an optimal balance between accuracy and computational efficiency remains the challenge of the beta testing period. Consequently, in forthcoming articles, we plan to broaden our validations to encompass larger-scale models with typical geometries. This expansion aims to facilitate meaningful comparisons with established standards and to provide comprehensive guidelines for efficient wind load generation post-processed from simulation results.
References:
[1] Dataprocessing and velocity-based validation on a simple block – https://consteelsoftware.com/ro/knowledgebase/dataprocessing-and-velocity-based-validation-on-a-simple-block/
[2] Baines, W. D., 1963. Effects of velocity distributions on wind loads and flow patterns on buildings, Proceedings, International Conference on Wind Effects on Buildings and Structures, Teddington, U.K., 26–28 June, 198–225
[3] Aerodynamic database for low-rise buildings – https://wind.arch.t-kougei.ac.jp/system/eng/contents/code/tpu
[4] EN 1991-1-4: Eurocode 1: Actions on structures – Part 1-4: General actions – Wind actions
In this second article of our wind simulation series, we will delve into two critical topics of wind simulation for structural engineering. The first one is data processing, a collective name for the most relevant steps of the fluid-dynamics aided wind load generation, such as mesh creation, executing the simulation itself and extracting initial results. While the second one is a preliminary velocity-based validation example to broadly explain the influence of the simulation parameters, to ensure that the results are accurate and useful for practical design applications.
In the previous article [1], we covered the preprocessing steps for wind simulation, including setting up the geometry using simulation surfaces and boundary conditions (wind effects and directions). These parameters were mostly aligned with the underlying logic of the standards, therefore their interpretation is relatively straightforward. However, to carry on it is inevitable to briefly introduce the simulation related parameters too, which are divided into two categories.
The basic settings are the ‘mesh size on structure’ and the ‘mesh refinement factor’. The first one is the average edge size on the structure for both of the generated meshes, the finite element mesh for mechanical and the the finite volume mesh for fluid-dynamical purposes, presented in the previous article. While the refinement factor is used to increase the finite volume cell edge sizes at the boundaries of the simulation domain, which are considered to be far enough from the building, therefore it is not necessary to calculate field values as densely as it is calculated around the building according to the ‘mesh size on structure’ parameter, leading to quicker simulations.
Note: Larger mesh size on the structure and larger refinement factor values are leading to coarser mesh, therefore a quicker simulation but less accurate results!
The advanced settings are a set of parameters to control the simulation in the background, with default values usually leading to adequate results. However the goal of this article is to provide an insight in their influence.
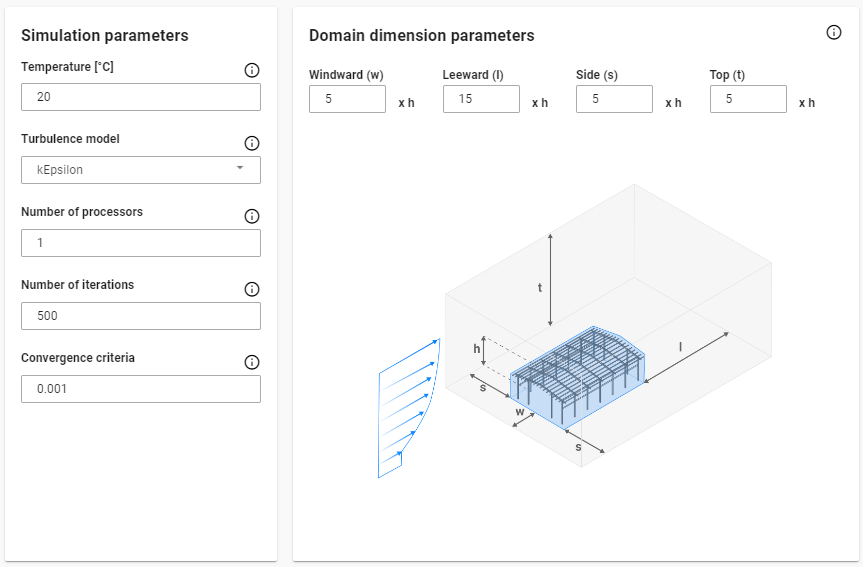
To ensure a meaningful validation, a wind tunnel test was replicated, utilizing experimental data and computational parameters from the Architectural Institute of Japan (AIJ) Benchmarks [2] . The experiment was carried out in a small circulatory wind tunnel at the Technical Research Institute of Shimizu Corporation. The test model consisted of an acrylic cuboid with dimensions of 160 mm in height and 80 mm in width. The inflow wind velocity was set at 6.75 m/s, with a measured turbulence intensity of approximately 0.5%.
Note: These validations were performed in a development version of our tool in the Grasshopper enviroment. In Consteel the tool focuses on the generation of wind loads, therefore can be utilized to extract pressure values.
Several key aspects were considered throughout the entire analysis process of the case study. Given that the model represents one of the simplest geometries encountered in practice, and that its structural behavior is straightforward to interpret within the context of standard guidelines, this case served multiple purposes. Primarily, it was used to underline the importance of conducting mesh independency tests prior to the actual simulation. As indicated in the table below, even for a simple geometry, the influence of mesh density proved to be significant — not only in terms of result accuracy but also from a performance perspective. For further investigations the “2000-4” mesh configurations was chosen, where the convergence of results became apparent.
| Mesh size on structure [m] | 8000 | 4000 | 2000 | 1000 |
| Mesh refinement factor | 2 | 3 | 4 | 5 |
| Meshing runtime [s] | 18.3 | 65.3 | 61.2 | 108.9 |
| Cell number [-] | 136432 | 150881 | 264786 | 495694 |
| Simulation runtime [s] | 65.3 | 57.9 | 151.1 | 343.4 |
| Iterations [-] | 264 | 182 | 260 | 314 |
| Fx+ [kN] | 197 | 203.0 | 205.6 | 203.5 |
| Fy+ [kN] | 94.4 | 94.5 | 89.9 | 89.7 |
| Fy- [kN] | 94.5 | 94.4 | 89.8 | 89.8 |
| Fz+ [kN] | 53.6 | 52.4 | 47.7 | 48.2 |
The next aspect was to emphasize the significance of mesh refinement, particularly along the edges. For example, finer mesh resolutions capture higher suction values on the side walls, though over smaller localized areas. Consequently, it is crucial to closely monitor the global reactions from the acting pressures influenced by a given mesh configuration, as presented in the table above.
Following the initial calibration tests, five different turbulence models (k – ε, k – ω, k – ω SST, RNG k – ε, Realizable k – ε) were compared based on their respective velocity fields.
These cases were executed simultaneously to assess the impact of full processor utilization. During the meshing process, the same mesh was applied in nearly all cases; however, the runtime increased to approximately 250 seconds, which is four times longer than when the cases were run separately. This clearly indicates that the previously reported runtimes were significantly influenced by the concurrent execution of parallel processes.
Note: It is also possible to run a single simulation case in parallel, which involves decomposing the computational domain and subsequently reconstructing it. However, this decomposition process also requires computational resources, meaning that running simulations in parallel does not always result in faster execution times.
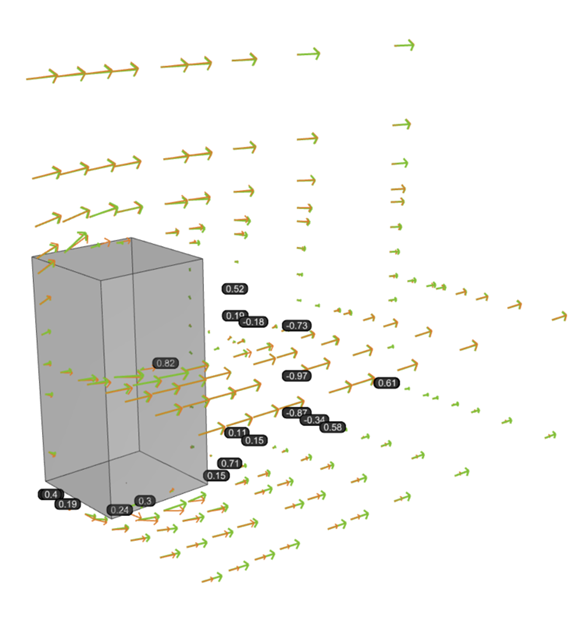
The primary metric used for each case was the average directional deviance of the velocity vectors obtained by simulation from the benchmark experiment velocity vector, where 0 indicates parallel vectors and 1 indicates perpendicular vectors. Across all scenarios, similar behavior was observed in the wake region of the building, underlining a key limitation of RANS-type turbulence models. Specifically, these models tend to capture only a single dominant vortex during flow separation, resulting in the highest deviations behind the building, as well as near the ground.
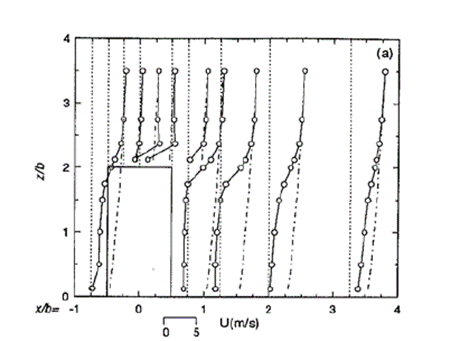
To assure relevant and transparent validations the original AIJ benchmark results were compared with the results obtained using several turburent models in a similar manner. A set of points close to the building inside of the calculation domain were monitorized.
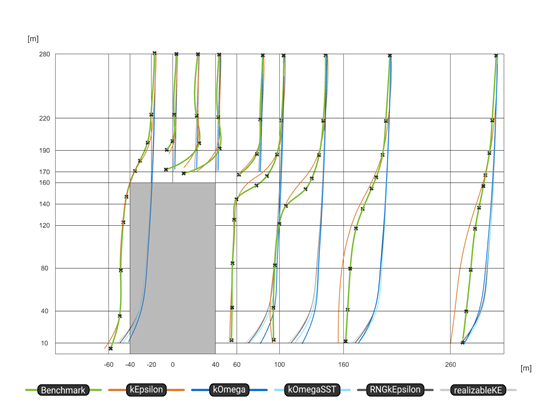
In conclusion, while these validations based on velocity fields may have limited direct relevance from a structural engineering perspective, understanding the flow behavior around buildings and calibrating simulations appropriately remains crucial. It is evident that even for simple geometries, simulation results are highly sensitive to parameter variations, underlining the need for an iterative approach to ensure mesh independence and result convergence.
During the investigation, the objective was to establish a general guideline for better starting values. As such, a mesh size on structure between e/12 and e/20 is recommended for the structure, where “e” corresponds to the minimum value between the crosswind width of the structure and twice its height, as defined in EC 1991-1-4 [3]. Using this as a starting point, it is advisable to apply an iterative simulation process with a refinement factor ranging from 5 to 0, while continuously monitoring the convergence of pressure results. This iterative method forms the foundation of the load generation procedure during the post-processing phase, which will be further discussed in upcoming knowledge base materials.
References:
[1] Preprocessing wind simulation for structural engineering purposes
[2] Guidebook for CFD Predictions of Urban Wind Environment – Architectural Institute of Japan
[3] EN 1991-1-4: Eurocode 1: Actions on structures – Part 1-4: General actions – Wind actions
As we prepare to publish the first version of our wind simulation tool, let’s explore the theoretical and technological background that makes it unique. Throughout the development process, we identified a significant gap between computational fluid dynamics and structural mechanics, highlighting a substantial amount of knowledge that needs to be bridged. With our commitment to fostering a responsible developer-user community, we’ve decided to release several knowledge base materials in the upcoming months to explain the key features that primarily will operate behind the scenes within the Consteel design workflow. The first step is to understand the prerequisites of the tool and how we aim to align the finite element, standard-based approach of structural engineering with the finite volume methods used in computational fluid dynamics. In short, we refer to this as preprocessing. So, let’s delve into what that entails.
In structural engineering, the evaluation of wind-induced loads is typically carried out using standard procedures designed to simplify the process in various ways. However, when more advanced methodologies like computational fluid dynamics are utilized, these standards inevitably serve as a benchmark, providing a basis for comparison against the pressure results generated by the simulation.
The entire development process was centered around determining wind profiles using standard procedures. The first implementation follows Eurocode 1-4, which is based on a set of parameters, organized similarly to the Consteel interface for defining meteorological effects.

The velocity pressure parameters include the basic wind velocity (vb), which can be selected based on geographical zones specific to each country, and the terrain category. The terrain category, as defined in a selected national annex, provides values for roughness length (z0), minimum height (zmin), and the terrain factor (kr). The terrain factor can either be a fixed value, as specified in several national annexes, or calculated using a proposed formula based on the roughness length and minimum height. Additionally, the selected national annex provides essential values for air density (ρ), orography coefficient (co(z)), and turbulence factor (kI), among others.
Internal pressure parameters include coefficients that modify the velocity pressures for a given wind direction, replicating the effects of internal pressures as described in the Eurocode.
Note: At this stage of development, we strongly recommend using the tool solely for achieving external pressure on closed, ‘air-tight’ buildings.
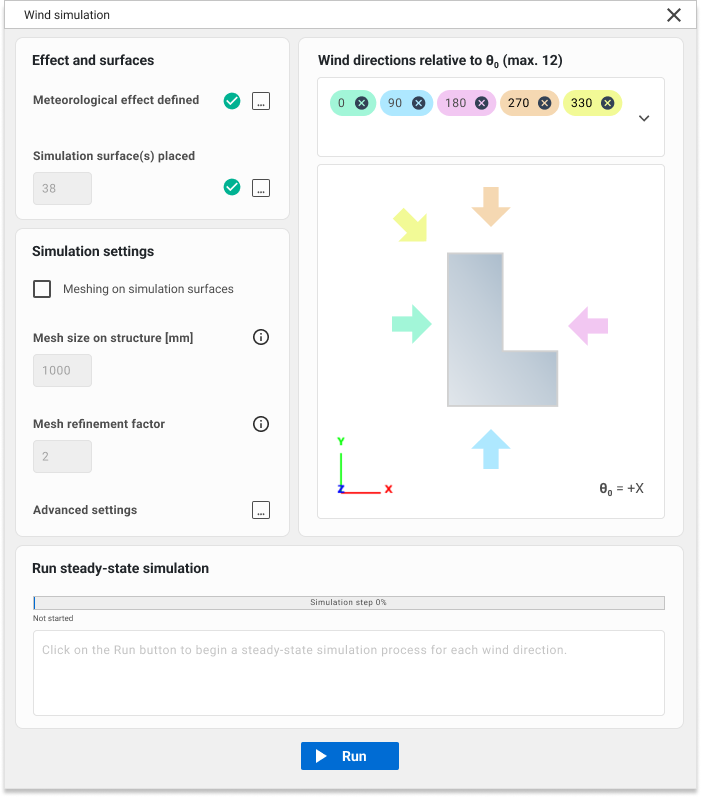
The geometric parameters include the basic wind direction definition according to the global coordinate system (θ = 0°), the ground level (Z), and other dimensional parameters. These parameters can be used to create zoned loads, allowing for load contours similar to those defined in the Eurocode.
Finally, simulation surfaces are the surfaces enclosing the investigated building. acting as load transfer surfaces for subsequent mechanical calculations.
Note: Currently, simulations are limited to surfaces and cannot be performed on beam members.
Once all the necessary parameters which are aligned with the underlying logic of the standards are collected, the actual preprocessing can be initiated from a separate dialog. This interface requires additional CFD-related inputs, which will be explained in the upcoming knowledge base materials.
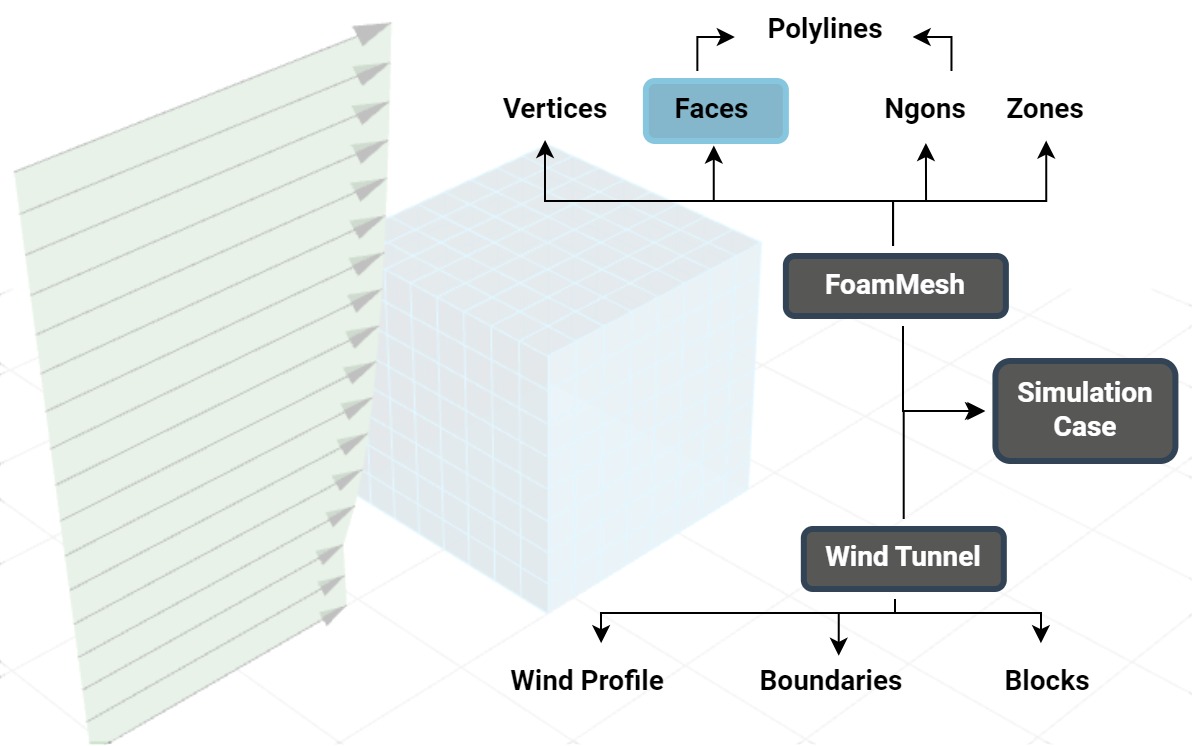
The preprocessor can be observed as an operational phase or a collection of methods, with two primary tasks executed based on the previously gathered parameters. The first task is to convert the input geometry into a specially developed mesh format (FoamMesh). This format resembles a traditional finite element mesh, featuring triangular or quadrilateral planar faces and vertices, and is capable of storing simulation results. Additionally, FoamMesh can interpret meshes with polygonal faces (‘Ngons’), typically generated by OPENFOAM®, which can often be non-planar. Besides, faces can also form zones based on their results. For representation purposes, these meshes can be viewed as a list of polylines (or two-dimensional figures in Consteel) at any time.
Note: The finite element mesh used for simulation differs from the mesh employed for load distribution in mechanical calculations. The internal vertices of this simulation-specific are obtained through the iterative offset of the surface contour, aiming to primarily create quadrilateral faces. These quad faces are preferred for zoned load creation during the postprocessing phase.
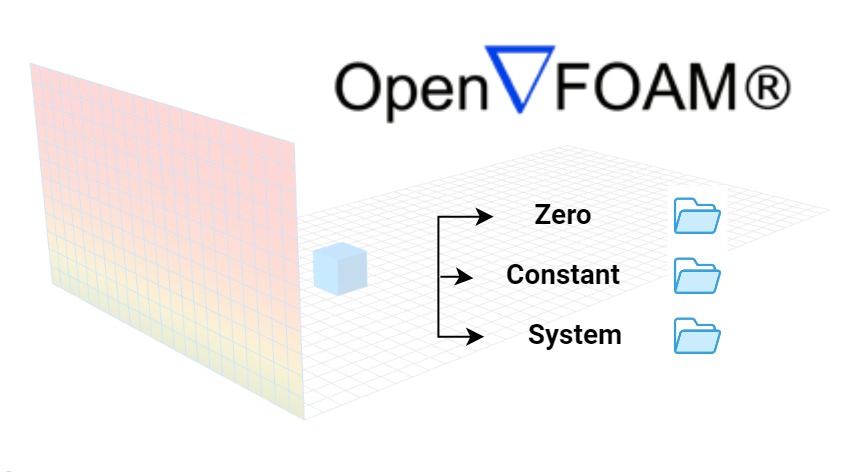
The other task is to generate a virtual wind tunnel, which consist of the wind profile according to the parameters, and the actual closed domain in which the simulation is performed defined by boundaries and inner blocks (finite volumes). Having these two it is possible to create the simulation case contents proper to the OPENFOAM® hierarchy. The wind flow parameters are stored in ‘zero’ folder, mesh generation both in ‘constant’ and ‘system’, while solution and result query parameters in ‘system’.
Note: For each wind direction a separate simulation case is performed, with it’s own independent finite volume mesh based wind tunnel. However, the finite element mesh of the building is identical, regardless the direction.
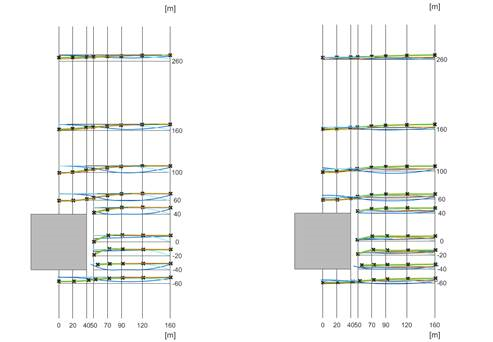
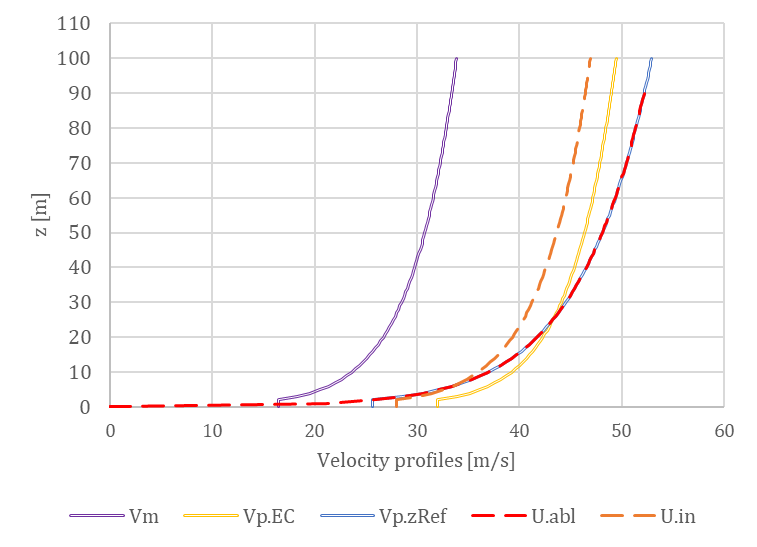
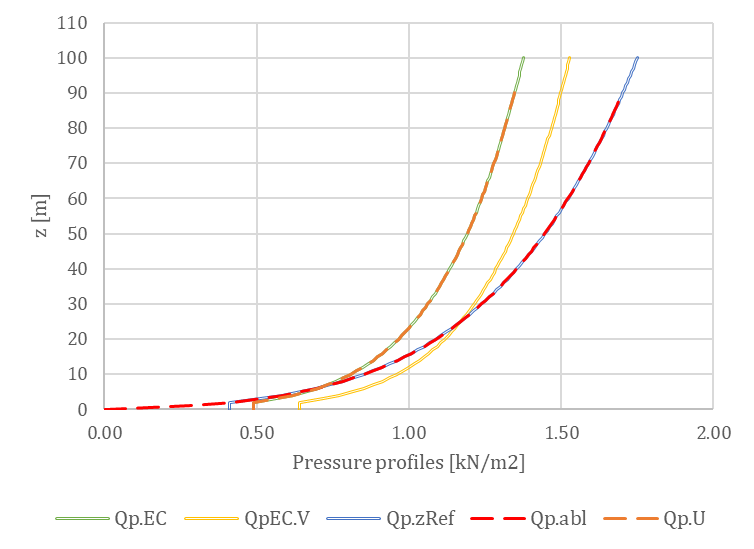
Regarding the wind profile, the clear objective is to introduce a wind velocity profile that replicates the peak pressure profile specified by the code. However, defining this profile is not straightforward. The figures below illustrates various approaches, with the QpEC function representing the general ‘target’ profile according to Eurocode.
Since Eurocode typically neglects the second-order term of turbulence intensity (considering only 1 + 7Iv(z)) when calculating QpEC, a significant difference arises if we calculate the velocity pressure, QpEC.V, from the peak velocity profile (using 1 + 3.5Iv(z) for turbulence intensity). As a result, VpEC is not intended to be directly implemented in OPENFOAM®.
Besides the standards, OPENFOAM® offers a default approach for logarithmic atmospheric boundary layers (Uabl), based on the friction velocity U* calculated at a reference height. However, the resulting Qp.abl also shows a significant difference, lacking the constant segment below the minimum height (zmin). Otherwise, this profile is similar to a standard Vp(zRef), which is evaluated along the height using only one exact turbulence intensity value calculated at the reference height (Iv(zref)).
The logarithmic profile evaluated by the atmospheric boundary layer approach of the OPENFOAM® is according to the followings:
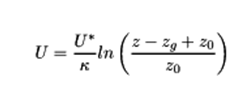
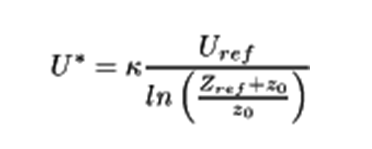
Therefore, it was necessary to develop a unique solution within OPENFOAM® for the determination of the Uin as the inlet peak velocity profile, which produces the desired QpEC. This uses the following formula:
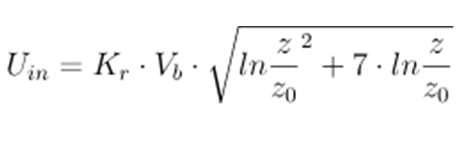
For an inlet wind profile using the k-ε turbulence model the initialization of the k and ε field values is also necessary. For this, there are also different approaches to consider. The basic atmospheric boundary layer of OPENFOAM® calculates a constant value along the height automatically, according to:
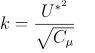
However, the inlet turbulent kinetic energy is generally calculated based on the inlet reference velocity and the turbulence intensity, which is defined by Eurocode according to the terrain parameters as presented previously:
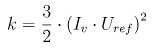
Similarly for the inlet ε there is a default automatic way used by the OpenFOAM based on the friction velocity:
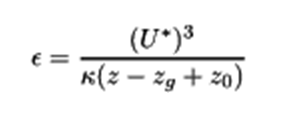
And there is also an approach considering the turbulent length intensity which can be evaluated according to a Eurocode procedure:
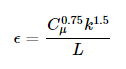
These approaches were compared for both the mean velocity and the peak velocity profiles, as shown in the figure below. The peak pressures correspond to the values measured on the windward wall of a simple 8 m x 8 m x 8 m cuboid. The naming conventions for the profiles are as follows: inlet velocity profile (mean and peak) – inlet turbulent kinetic energy (automatic – a or calculated – c) – inlet turbulent dissipation rate (automatic – a or calculated – c).
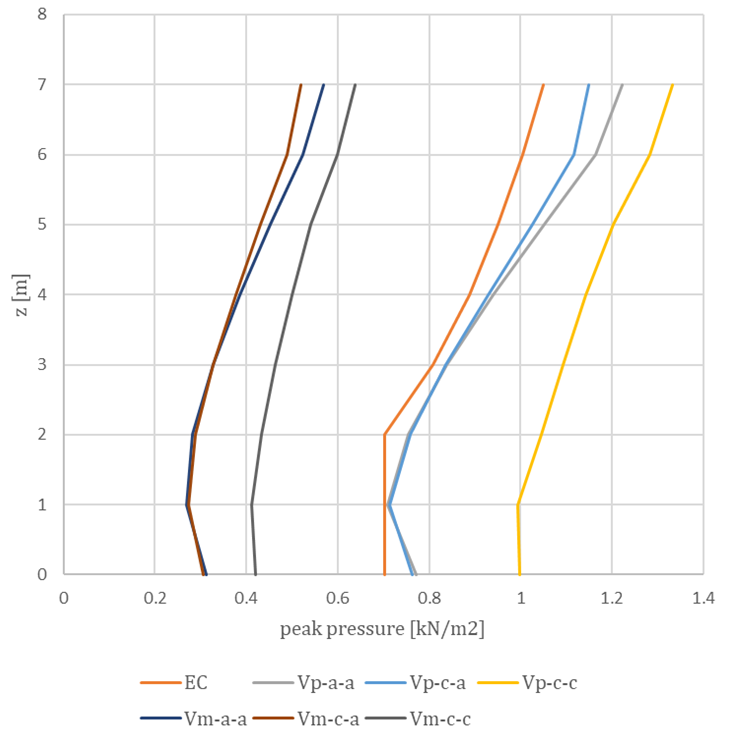
In conclusion, the profile chosen for implementation is the Uin, with automatic evaluation applied to both the inlet turbulent kinetic energy (k) and the inlet turbulent dissipation rate (ε). The effects of various turbulence models, along with the influence of different meshing procedures on the geometry, to which we refer as dataprocessing, will be discussed in upcoming knowledge base materials. So stay tuned as we explore different validations of this newly developed tool.
